オープンソースのデジタル画像相関 による 腱の局所組織ひずみの測定

要約

この論文では、腱の外植片内の局所的な2D組織ひずみを測定するためのオープンソースのデジタル画像相関アルゴリズムについて説明します。この手法の精度は、複数の手法を使用して検証されており、一般に利用できます。

要約

腱細胞がその 場で 経験する株と、これらの株が組織のリモデリングにどのように影響するかを理解することには、かなりの科学的関心があります。この関心に基づいて、負荷中に腱外植片内の局所組織株を測定するためのいくつかの分析技術が開発されてきた。ただし、いくつかのケースでは、これらの手法の精度と感度は報告されておらず、どのアルゴリズムも公開されていません。これにより、腱の外植片における局所組織株のより広範な測定が困難になりました。したがって、この論文の目的は、腱外植片の局所組織株を測定するための検証済みの分析ツールを作成することでした。具体的には、公開されている拡張ラグランジュデジタル画像相関(ALDIC)アルゴリズムを、一軸張力下でマウスアキレス腱内の細胞核の変位を追跡することにより、2D株を測定するために適合されました。さらに、計算されたひずみの精度は、デジタル変換された画像を分析することによって、および株を独立した技術(すなわち、光漂白線)から決定された値と比較することによって検証されました。最後に、計算された変位場を使用して参照画像を再構築する手法がアルゴリズムに組み込まれ、既知のひずみ値がない場合のアルゴリズムの精度を評価するために使用できる、または二次測定技術。このアルゴリズムは、0.00015の精度で最大0.1のひずみを測定できます。再構成された参照画像と実際の参照画像を比較する手法は、誤ったデータを持つサンプルを特定することに成功し、良好なデータを持つサンプルでは、変位場の約85%が正確であることを示しました。最後に、マウスのアキレス腱で測定された株は、以前の文献と一致していました。したがって、このアルゴリズムは、腱の局所組織ひずみを正確に測定するための非常に有用で適応性のあるツールです。

概要

腱は、機械的負荷に応答して適応および変性する機械感受性組織^です1,2,3,4。腱細胞の生物学において機械的刺激が果たす役割のために、腱細胞が負荷中に天然の組織環境で経験する株を理解することに大きな関心があります。腱の局所組織株を測定するために、いくつかの実験的および分析的技術が開発されている。これらには、スペックルパターンまたはフォトブリーチングライン(PBL^{)のいずれか}を使用した表面ひずみの2D/3Dデジタル画像相関(DIC)分析5,6,7,8、組織内の個々の核の重心間距離の変化の測定^9,10、および面外運動と3D変形を考慮した最近のフルフィールド3D DIC法が含まれます¹¹.しかし、これらの手法の精度や感度はごくわずかしか報告されておらず、いずれも公開されていないため、普及・活用は困難である。

この研究の目的は、腱外植片の局所組織株を測定するための検証済みの分析ツールを作成することでした。選択された方法は、YangとBhattacharya¹²によって開発されたMATLABで書かれた公開されている拡張ラグランジュデジタル画像相関(ALDIC)アルゴリズムに基づいています。このアルゴリズムは、腱サンプルの分析に適合し、デジタル変換された画像に適用し、実際の腱サンプルで測定されたひずみを光退色の線から得られた結果と比較することによって検証されました。さらに、既知のひずみ値や二次測定技術がない場合でも、計算された変位場の精度を確認するための追加機能がアルゴリズムに実装されました。したがって、このアルゴリズムは、腱の局所2D組織ひずみを正確に測定するための非常に有用で適応性のあるツールです。

プロトコル

この研究は、ペンシルベニア州立大学の施設動物管理および使用委員会によって承認されました。

1.ティッシュの準備

1. このプロトコルでは、生後2〜4か月のオスのC57BL / 6マウスからアキレス腱を採取します。
   注:マウスや他の小動物とは異なる腱や靭帯を使用することもできます。
   1. アキレス腱の表在性皮膚を切開して、足底腱と周囲の結合組織を露出させます。次に、外科用ブレードを使用してそれらを取り外します。
   2. 露出したヒラメ筋と腓腹筋を後肢から分離し、手術用ブレードでアキレス腱から慎重にこすり落とします
   3. 回転工具のカッティングホイールアタッチメントを使用して、踵骨を足の残りの部分から分離します。
2. 5-(4,6-ジクロロトリアジニル)アミノフルオレセイン(DTAF)と0.1 M重炭酸ナトリウムバッファーの5 μg/mL溶液1.5 mLで、室温の回転ミキサーで20分間組織を染色します。この溶液は、組織内のタンパク質(例えば、細胞外マトリックス)を染色する。
   注: この 20 分間の間に、手順 1.3 を完了する必要があります。
3. リン酸緩衝生理食塩水(PBS)中のDRAQ5の1:1,000溶液を調製して、核を染色します。ボルテックスミキサーを使用して溶液を均質化します。
4. ステップ1.2の20分間のインキュベーション期間の後、組織をDTAF溶液からDRAQ5溶液に移し、暗所で室温で10分間インキュベートします。

2. 腱負荷と画像取得

注:このプロトコルには、共焦点顕微鏡の上に取り付けることができる引張装置が必要です。この研究では、PetersonとSzczesny¹³ によって記述された微小引張装置が使用されました。

1. 腱を引張荷重装置のグリップに配置します。グリップをローディングデバイスに取り付ける前に、デジタルキャリパーを使用して、踵骨アタッチメントと反対側のグリップの間の距離を測定します。この距離が腱ゲージ長です。
   1. または、腱を挿入する前にグリップをローディングデバイスに取り付け、接触させてゼロ変位モーターの位置を定義します。腱を挿入した後のモーターの変位は、潜在的により正確なグリップツーグリップゲージ長を提供する可能性があります。
2. 組織の水分補給を維持するためにPBSを含むローディングデバイスにグリップを取り付けます。アルゴリズムのx系統とyひずみの出力が腱の軸と一致するように、腱を顕微鏡画像のx軸またはy軸のいずれかにできるだけ合わせます。
   注:この研究では、腱はx軸に整列していました。腱を画像軸と完全に整列させることが不可能な場合は、標準ひずみ変換式¹⁴を使用して、アルゴリズムのxひずみおよびyひずみ出力を腱の縦軸/垂直軸に整列するように変換できます。
3. 腱に1 gの張力をかけ、必要に応じて周期的な負荷を加えてサンプルを事前調整します。このプロトコルでは、研究の目的は組織材料特性を測定するのではなく、測定された局所組織株を検証することであったため、事前調整は使用されていません。荷重履歴に依存するマクロスケールの材料特性の測定に関心がある場合は、事前調整をお勧めします。プレコンディショニングと回復に続いて、1gのプリロードを再適用します。
4. 必要に応じて、組織の中央領域で80μm間隔で4本のラインのセットを光退色します(詳細については、Peterson and Szczesny¹³ を参照してください)。
   注:フォトブリーチラインは、ALDICアルゴリズムの測定を検証するために使用され、ALDIC自体を実行するためには必要ありません。線の数と間隔は調整でき、線の位置を選択して、線の明瞭さを低下させるサンプル内のアーティファクトを回避する必要があります。
5. グリップの近くの組織の左右の端で光退色手順を繰り返します。
6. 共焦点顕微鏡を使用して、1 gのプリロードでDTAFおよびDRAQ5蛍光の体積画像(x、y:1.25 μm/ピクセル、z:2.5 μm/ピクセル)を取得します。
7. 0.5%/sから2%のひずみでひずみランプを実行します。ひずみ速度と増分ひずみの大きさは調整できることに注意してください。
8. 組織を10分間リラックスさせます。
   注意: 応力緩和の持続時間は、画像取得中にサンプルがほぼ準静的な負荷を受けるように選択する必要があります。応力緩和期間が許容範囲内かどうかを判断するには、応力緩和の最後の1分間の力-時間曲線の傾きを決定し(補足図1)、この傾きに合計イメージング時間を掛けます。この研究では、最大ひずみ増分で加えられた力は5%を超えて変化することはありませんでした。
9. 変形後の組織の別の体積画像を撮影します。
10. 目的の最終ひずみに達するまで、手順2.7〜2.9を繰り返します。この論文では、12%の最終ひずみ値を選択しました。

3. 画像処理

1. ImageJ またはフィジーを使用して、DRAQ5 (核) チャネルの各体積イメージの最大 Z 投影を作成します。これは、ALDICの2D斑点画像として機能します。
2. 最大強度の Z 投影を.tiffファイルとして保存し、次の命名規則に従って名前を付けます。
   1. イメージ名の最初の文字として数字を使用します。
   2. この番号は、ひずみ解析中に画像が考慮される順序に対応させます。たとえば、最初の画像は 1 で始まり、2 番目の画像は 2 で始まる必要があります。異なる数値を選択できますが、順番に増やす必要があります。命名規則の例は、"0_Experiment1_MaxZProjection" です。
3. 名前を変更したすべての最大強度 Z 投影法をフォルダーに保存します。

4. 光漂白ライン解析コードのインストールと応用

注:これらの手順は、フォトブリーチラインを使用してALDICアルゴリズムの精度を確認する場合にのみ必要です。このコードは、局所組織ひずみを、フォトブリーチされたラインセット内の各フォトブリーチライン間の距離の平均正規化変化として計算します。この研究では、次に、すべての光退色ラインセット(つまり、中央と左/右端)の平均局所値を平均して、各サンプルの単一の平均局所組織ひずみ値を決定しました。次に、この値を使用してALDICアルゴリズムの精度を推定しました。

1. GitHub (https://github.com/Szczesnytendon/TendonStrainCalc) から "PBL コード" フォルダーをダウンロードし、すべてのコンテンツを MATLAB の作業ディレクトリに移動します。
2. "Micro_Mech_Template.m" MATLAB スクリプトを開きます。
   1. [実行]を押して、ボリューメトリック画像を含む画像ファイルの1つを選択します。ボリューメトリック イメージは、.lsm、.tiff、.nd2 のいずれかのファイル形式にすることができます。
   2. ソフトウェアは自動的にフォルダ内のすべての画像をロードし、基準体積画像の投影画像を表示します。プロンプトが表示されたら、左 クリックして 、サンプルの左端と右端をトレースするマルチポイントラインを作成します。 右クリック して行を終了します。入力が処理され、エッジが正しい場合は、[ OK] を押して結果を受け入れます。
   3. プロンプトが表示されたら、サンプルを横切るランダムな対角線を参照線として描画します。
   4. 作成したフォトブリーチングラインの数を入力し、マルチポイントラインでフォトブリーチングラインをトレースします。
   5. 結果が許容できる場合は、それを受け入れます。結果が誤っている場合は、調整して再処理します。
3. すべての画像に対して手順 4.2 を繰り返し、トレースされた線のすべての画像を 1 つのフォルダーに移動します。
4. スクリプト "Micro_Mech_Strain.m" を開きます。
   1. [実行]を押してコードを実行し、フォトブリーチされた線がトレースされている保存済み画像の1つを選択します。
   2. 画像を選択したら、選択した付随画像が正しいことを確認し、 OKを押します。

5.デジタル変換された画像の作成

注:これらの手順は、デジタル変換された画像を使用してALDICアルゴリズムの精度を確認する場合にのみ必要です。これらの画像は、参照画像を人為的に変換することにより、既知の大きさの均質な2Dひずみ場をシミュレートします。

1. GitHub (https://github.com/Szczesnytendon/TendonStrainCalc) からコード "Digital_strain.m" をダウンロードします。
2. コードを開いて実行します。
3. プロンプトが表示されたら、最大適用ひずみ、適用ひずみ増分、およびポアソン比に必要な値を挿入します。 OKを押します。
   注:この実験では、最大適用ひずみは0.1(10%)、適用ひずみ増分は0.02(2%)、ポアソン比1を使用し、これは腱引張試験の実験データと一致しています^15,16。このコードでは、埋め込まれたMATLAB関数のインワープと入力値(ひずみ増分、ポアソン比など)を使用して、デジタル変換された画像を作成します。
4. プロンプトが表示されたら、変形されていない参照イメージを選択します。
5. ひずみ増分ごとに、参照画像と変換後の画像のオーバーレイが表示されます。変換された画像は、「デジタル変換X%ひずみ」というタイトルのディレクトリに保存されます(Xはひずみ増分)。

6. ひずみ計算・検証コードのインストールと応用

1. GitHub (https://github.com/Szczesnytendon/TendonStrainCalc) から "ひずみ計算と検証コード" フォルダーをダウンロードし、すべての内容を MATLAB 作業ディレクトリに移動します。
2. ヤンとバッタチャリヤ¹²に従ってmex C / C ++コンパイラをインストールします。手順を以下にまとめます。
   1. MATLAB コマンド ウィンドウに「mex -setup」と入力して Enter キーを押して、mex C/C++ コンパイラがインストールされているかどうかを確認するために MATLAB をチェックします。
   2. コンパイラーがサポートされていない、または存在しないことを示すエラーが表示された場合は、ステップ 6.3 およびステップ 6.4 に進みます。
   3. エラーが存在しない場合は、手順 6.5 に進みます。
3. mex C/C++ コンパイラをダウンロードするには、"https:/tdm-gcc.tdragon.net/" にアクセスし、TDM-gcc コンパイラを選択します。
4. ダウンロードしたコンパイラを既知の場所にインストールします。
5. MATLAB コマンド ウィンドウに戻り、" setenv("MW_MINGW64_LOC","[ここにインストール パスを入力してください]")" と入力します。 たとえば、"setenv("MW_MINGW64_LOC","C:\TDM-GCC-64")" などです。このコマンドが正常に実行されると、mex コンパイラが正しくインストールされます。
6. 「main_aldic.m」関数スクリプトを入力し、ステップ 6.5 で実行したコマンドと一致するように 22 行目を変更します。
7. スクリプト "Strain_calc_and_validate.m" を開きます。
8. [実行] を押して、画像解析を開始します。
9. プロンプトが表示されたら、必要に応じて ALDIC パラメーターの値を変更します。
   注: ウィンドウ サイズは、サブセット サイズの 0.25 倍から 1 倍にする必要があります。パラメータの選択の詳細については、オンラインユーザーマニュアルを参照してください:(https://www.researchgate.net/publication/344796296_Augmented_Lagrangian_Digital
   _Image_Correlation_AL-DIC_Code_Manual)。
   1. この研究では、次の値を使用しました。
      サブセットサイズ(ピクセル): 20
      ウィンドウサイズ(ピクセル): 10
      ALDICを解く方法:有限差分(1)
      並列計算は使用されなかった (1)
      初期推測の計算方法: 画像ピラミッドに基づくマルチグリッド検索 (0)
10. プロンプトが表示されたら、「はい」チェックボックスを選択すると、アルゴリズムは、目的の変数のコレクション(xひずみ、yひずみ、せん断ひずみ、不良領域など)の平均値、標準偏差、および2Dマップを自動的に保存します。保存する変数を選択し、[ OK]を押します。
11. プロンプトが表示されたら、必要に応じてパラメーターを変更します。
    1. この実験では、次の値を使用しました。
       ひずみを計算するための周辺点(numP):12
       不良領域識別の相関係数 (corr_threshold): 0.5
       不良領域分析のサブ領域サイズ (ピクセル) (サブサイズ): 32
12. プロンプトが表示されたら、名前を変更した最大強度 Z 投影を含むフォルダーを選択します。ソフトウェアは自動的にインクリメンタルALDICを実行して、変形画像のひずみ場を決定することに注意してください。すなわち、各変形画像は、次の変形画像の新しい「参照」画像として機能する。これにより、各変形画像が元の(0%ひずみ)参照画像と比較される累積ALDICを実行する場合と比較して、結果の精度が向上します(補足図2)。累積解析を実行するには、画像を読み込みますが、元の参照画像と目的の変形画像のみを選択します。
    注: 正規ひずみは λ - 1 として計算されます (λ は組織の伸びです)。組織の伸張は、x方向とy方向にそれぞれN = [1 0]Tまたは[0 1]^T、およびC = F F F(^FはALDICアルゴリズムによって出力された各データポイントを囲む「numP」ポイントを使用して計算された変形勾配)に従って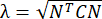計算されます。せん断ひずみは次のように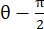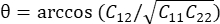計算されます。
13. プロンプトが表示されたら、左クリックして 4 点ポリゴンを作成し、ひずみを測定するための関心領域を定義します。左上隅のポイントから始めて、後続のポイントを時計回りに割り当てます。
    注: MATLAB ワークスペースに保存されている変数「ストレージ」には、平均 x ひずみ、x ひずみ標準偏差、平均 y ひずみ、y ひずみ標準偏差、平均せん断ひずみ、せん断ひずみ標準偏差、および不良領域の割合のすべての値が含まれています。不良領域は、ステップ6.13で選択された関心領域内の相関係数分析に従って定義されます。フォルダ「NuclearTrackingResults」(555行目と556行目を調整することで名前を変更できます)には、手順6.10で指定されたすべてのプロットが保存されます。このフォルダには、ステップ6.10で指定されたすべての平均と標準偏差を格納する「Results」という名前のスプレッドシートファイルも含まれています。

結果

実際の組織サンプルのひずみ場を分析する前に、ALDICプロトコルは、マウスのアキレス腱内の核のデジタルひずみ/変換画像を使用して最初に検証されました。具体的には、画像をデジタル変換して、シミュレートされたポアソン比1 ^15,16で、x方向に2%、4%、6%、8%、および¹⁰%の均一なひずみを生成します。次に、ALDICアルゴリズムの精度は、計算され?...

ディスカッション

この論文の目的は、引張荷重下で腱の2Dひずみ場を測定するためのオープンソースの検証済み方法を提供することでした。ソフトウェアの基礎は、公開されているALDICアルゴリズム¹²に基づいていました。このアルゴリズムは、インクリメンタル(累積)ひずみ解析の機能が追加され、より大きなMATLABコードに埋め込まれました。次に、この適応アルゴリズムを腱の引張試験に?...

資料

Name	Company	Catalog Number	Comments
5-DTAF (5-(4,6-Dichlorotriazinyl) Aminofluorescein), single isomer	ThermoFisher	D16
Calipers	Mitutoyo	500-196-30
Confocal Microscope	Nikon	A1R HD
Corning LSE Vortex Mixer	Coning	6775
DRAQ5 Fluorescent Probe Solution (5 mM)	ThermoFisher	62554
MATLAB	MathWorks	R2022b
Tensile Loading Device	N/A	N/A	Tensile loading device described in Peterson et al, 2020. (ref 13)
Tube Revolver Rotator	ThermoFisher	88881001