Measuring Local Tissue Strains in Tendons via Open-Source Digital Image Correlation

Summary

This paper describes an open-source digital image correlation algorithm for measuring local 2D tissue strains within tendon explants. The accuracy of the technique has been validated using multiple techniques, and it is available for public use.

Abstract

There is considerable scientific interest in understanding the strains that tendon cells experience in situ and how these strains influence tissue remodeling. Based on this interest, several analytical techniques have been developed to measure local tissue strains within tendon explants during loading. However, in several cases, the accuracy and sensitivity of these techniques have not been reported, and none of the algorithms are publicly available. This has made it difficult for the more widespread measurement of local tissue strains in tendon explants. Therefore, the objective of this paper was to create a validated analysis tool for measuring local tissue strains in tendon explants that is readily available and easy to use. Specifically, a publicly available augmented-Lagrangian digital image correlation (ALDIC) algorithm was adapted for measuring 2D strains by tracking the displacements of cell nuclei within mouse Achilles tendons under uniaxial tension. Additionally, the accuracy of the calculated strains was validated by analyzing digitally transformed images, as well as by comparing the strains with values determined from an independent technique (i.e., photobleached lines). Finally, a technique was incorporated into the algorithm to reconstruct the reference image using the calculated displacement field, which can be used to assess the accuracy of the algorithm in the absence of known strain values or a secondary measurement technique. The algorithm is capable of measuring strains up to 0.1 with an accuracy of 0.00015. The technique for comparing a reconstructed reference image with the actual reference image successfully identified samples that had erroneous data and indicated that, in samples with good data, approximately 85% of the displacement field was accurate. Finally, the strains measured in mouse Achilles tendons were consistent with the prior literature. Therefore, this algorithm is a highly useful and adaptable tool for accurately measuring local tissue strains in tendons.

Introduction

Tendons are mechanosensitive tissues that adapt and degenerate in response to mechanical loading^1,2,3,4. Due to the role that mechanical stimuli play in tendon cell biology, there is a large interest in understanding the strains that tendon cells experience in the native tissue environment during loading. Several experimental and analytical techniques have been developed to measure local tissue strains in tendons. These include 2D/3D digital image correlation (DIC) analyses of surface strains using either speckle patterns or photobleached lines (PBLs)^5,6,7,8, measurement of the changes in the centroid-to-centroid distance of individual nuclei within the tissue^9,10, and a recent full-field 3D DIC method that considers out-of-plane motion and 3D deformations¹¹. However, the accuracy and sensitivity of these techniques have been reported in only a few cases, and none of these techniques have been made publicly available, which makes the widespread adoption and utilization of these techniques difficult.

The objective of this work was to create a validated analysis tool for measuring local tissue strains in tendon explants that is readily available and easy to use. The chosen method is based on a publicly available augmented-Lagrangian digital image correlation (ALDIC) algorithm written in MATLAB that was developed by Yang and Bhattacharya¹². This algorithm was adapted for analyzing tendon samples and validated by applying it to digitally transformed images and by comparing the strains measured in actual tendon samples to the results obtained from photobleached lines. Furthermore, additional functionality was implemented in the algorithm to confirm the accuracy of the calculated displacement field even in the absence of known strain values or a secondary measurement technique. Therefore, this algorithm is a highly useful and adaptable tool for accurately measuring local 2D tissue strains in tendons.

Protocol

This study was approved by the Pennsylvania State University Institutional Animal Care and Use Committee.

1. Tissue preparation

1. For this protocol, harvest the Achilles tendons from 2-4 month old male C57BL/6 mice.
   NOTE: Different tendons or ligaments from mice or other small animals could also be used.
   1. Make an incision to the skin superficial to the Achilles tendon to expose the plantaris tendon and the surrounding connective tissue. Then, remove them using a surgical blade.
   2. Separate the exposed soleus and gastrocnemius muscles from the hind limb, and carefully scrape them off the Achilles tendon with the surgical blade
   3. Separate the calcaneus from the rest of the foot with a cutting wheel attachment on a rotary tool.
2. Stain the tissue in 1.5 mL of a 5 µg/mL solution of 5-(4,6-dichlorotriazinyl) aminofluorescein (DTAF) and 0.1 M sodium bicarbonate buffer for 20 min on a rotating mixer at room temperature. This solution stains proteins (e.g., extracellular matrix) in the tissue.
   NOTE: During this 20 min period, step 1.3 should be completed.
3. Prepare a 1:1,000 solution of DRAQ5 in phosphate-buffered saline (PBS) to stain the nuclei. Use a vortex mixer to homogenize the solution.
4. After the 20 min incubation period in step 1.2, transfer the tissue from the DTAF solution to the DRAQ5 solution, and incubate in a dark space for 10 min at room temperature.

2. Tendon loading and image acquisition

NOTE: This protocol requires a tensile device that can be mounted on top of a confocal microscope. For this study, the microtensile device described by Peterson and Szczesny¹³ was used.

1. Place the tendon into the grips of the tensile loading device. Prior to mounting the grips in the loading device, use digital calipers to measure the distance between the calcaneus attachment and the opposite grip. This distance is the tendon gauge length.
   1. Alternatively, mount the grips into the loading device prior to inserting the tendon, and push into contact to define the zero-displacement motor position. The displacement of the motors after inserting the tendon could provide a potentially more accurate grip-to-grip gauge length.
2. Mount the grips into the loading device, which contains PBS to maintain tissue hydration. Align the tendon as best as possible with either the x-axis or y-axis of the microscope images so that the x-strain and y-strain outputs of the algorithm correspond with the tendon axes.
   ​NOTE: In this study, the tendons were aligned with the x-axis. If it is not possible to perfectly align the tendon with the image axes, then the x-strain and y-strain outputs of the algorithm can be transformed to align with the longitudinal/perpendicular axes of the tendon using standard strain transformation equations¹⁴.
3. Preload the tendon with 1 g of tension, and, if desired, apply cyclic loading to precondition the sample. In this protocol, no preconditioning was used since the study objective was to validate the measured local tissue strains rather than measure the tissue material properties. If there is interest in measuring the macroscale material properties, which are dependent on the loading history, then preconditioning is recommended. Following preconditioning and recovery, reapply a 1 g preload.
4. If desired, photobleach a set of four lines spaced 80 µm apart in the center region of the tissue (see Peterson and Szczesny¹³ for more details).
   NOTE: The photobleached lines were used to validate the measurements of the ALDIC algorithm and are not necessary for performing the ALDIC itself. The number and spacing of the lines can be adjusted, and the location of the lines should be chosen to avoid any artifacts in the sample that would decrease the clarity of the line.
5. Repeat the photobleaching procedure on the left and right extremes of the tissue near the grips.
6. Using the confocal microscope, acquire volumetric images (x,y: 1.25 µm/pixel, z: 2.5 µm/pixel) of the DTAF and DRAQ5 fluorescence at 1 g of preload.
7. Perform a strain ramp at 0.5%/s to 2% strain. Note that the strain rate and incremental strain magnitude can be adjusted.
8. Allow the tissue to stress relax for 10 min.
   NOTE: The duration of stress relaxation should be chosen such that the sample is under an approximately quasistatic load during image acquisition. To determine if the stress relaxation duration is acceptable, determine the slope of the force-time curve during the final minute of stress relaxation (Supplementary Figure 1), and multiply this slope by the total imaging duration. In this study, the force applied at the largest strain increment never changed by more than 5%.
9. Take another volumetric image of the tissue after deformation.
10. Repeat steps 2.7-2.9 until the desired final strain is reached. In this paper, a final strain value of 12% was chosen.

3. Image processing

1. Use ImageJ or Fiji to create maximum z-projections of each volumetric image of the DRAQ5 (nuclear) channel. This will serve as the 2D speckled images for the ALDIC.
2. Save the max-intensity z-projections as .tiff files, and name them according to the following naming convention.
   1. Use a number as the first character of the image name.
   2. Have the number correspond to the order in which the images will be considered during the strain analysis. For example, the first image should begin with one, and the second image should begin with two. Different numbers can be chosen, but they must sequentially increase. An example naming convention is as follows: "0_Experiment1_MaxZProjection".
3. Save all the renamed max-intensity z-projections to a folder.

4. Photobleached line analysis code installation and application

NOTE: These steps are only necessary if it is desired to confirm the accuracy of the ALDIC algorithm using photobleached lines. The code calculates the local tissue strain as the average normalized change in distance between each photobleached line within the photobleached line set. In this study, the average local values were then averaged across all the photobleached line sets (i.e., at the center and the left/right ends) to determine a single average local tissue strain value for each sample. This value was then used to estimate the accuracy of the ALDIC algorithm.

1. Download the "PBL Code" folder from GitHub (https://github.com/Szczesnytendon/TendonStrainCalc), and move all the contents to the working directory in MATLAB.
2. Open the "Micro_Mech_Template.m" MATLAB script.
   1. Press Run, and select one of the image files containing the volumetric images. The volumetric images can be any of the following file types: .lsm, .tiff, .nd2.
   2. The software will automatically load all the images in the folder and display a projected image of the reference volumetric image. When prompted, left-click to create multi-point lines that trace the left and right ends of the sample. Right-click to terminate a line. Once the input has been processed, if the edges are correct, press Ok to accept the result.
   3. Draw a random diagonal line across the sample as a reference line when prompted.
   4. Input the number of photobleached lines created, and trace the photobleached lines with multi-point lines.
   5. If the result is acceptable, accept it. If the result is erroneous, adjust it and reprocess.
3. Repeat step 4.2 for all the images, and move all the images of traced lines into a single folder.
4. Open the script "Micro_Mech_Strain.m".
   1. Press Run to execute the code, and select one of the saved images where the photobleached lines are traced.
   2. Confirm that the selected accompanying images are correct once the image is selected by pressing Ok.

5. Creating digitally transformed images

NOTE: These steps are only necessary if it is desired to confirm the accuracy of the ALDIC algorithm using digitally transformed images. These images simulate homogenous 2D strain fields of a known magnitude by artificially transforming the reference image.

1. Download the code "Digital_strain.m" from GitHub (https://github.com/Szczesnytendon/TendonStrainCalc).
2. Open and run the code.
3. When prompted, insert desired values for the maximum applied strain, applied strain increment, and Poisson's ratio. Press Ok.
   NOTE: For this experiment, the maximum applied strain was 0.1 (10%), the applied strain increment was 0.02 (2%), and a Poisson's ratio of 1 was used, which is consistent with experimental data of tendon tensile testing^15,16. The code uses the embedded MATLAB function imwarp and the input values (e.g., strain increments, Poisson's ratio) to create the digitally transformed images.
4. When prompted, select the undeformed reference image.
5. For each strain increment, an overlay of the reference image and the transformed image is displayed. The transformed image will be saved to the directory under the title "DigitallyTransformedX%Strain", where X is the strain increment.

6. Strain calculation and validation code installation and application

1. Download the "Strain Calculation and Validation Code" folder from GitHub (https://github.com/Szczesnytendon/TendonStrainCalc), and move all the contents to the MATLAB working directory
2. Install a mex C/C++ compiler according to Yang and Bhattacharya¹². The steps are summarized below.
   1. Check MATLAB to see if a mex C/C++ compiler has been installed by typing "mex -setup" in the MATLAB Command Window and pressing Enter.
   2. If an error appears indicating that a compiler is not supported or present, proceed to step 6.3 and step 6.4.
   3. If no error is present, proceed to step 6.5
3. To download a mex C/C++ compiler, go to "https:/tdm-gcc.tdragon.net/", and choose the TDM-gcc compiler.
4. Install the downloaded compiler to a known location.
5. Return to the MATLAB command window, and type: "setenv("MW_MINGW64_LOC","[Type your install path here]")". For example, this could be "setenv("MW_MINGW64_LOC","C:\TDM-GCC-64")". If this command executes successfully, the mex compiler is properly installed.
6. Enter the "main_aldic.m" function script, and change line 22 to match the command executed in step 6.5.
7. Open the script "Strain_calc_and_validate.m".
8. Press Run to begin the image analysis.
9. When prompted, alter the values for the ALDIC parameters as desired.
   NOTE: The window size should be 0.25 to 1 times the subset size. For more information about the parameter choices, refer to the online user manual: (https://www.researchgate.net/publication/344796296_Augmented_Lagrangian_Digital
   _Image_Correlation_AL-DIC_Code_Manual). 
   1. The following values were used in this study:
      Subset Size (pixels): 20
      Window Size (pixels): 10
      Method to solve ALDIC: Finite Difference (1)
      Parallel computing was not used (1)
      Method to compute initial guess: Multigrid search based on image pyramid (0)
10. When prompted, select the "Yes" checkbox to have the algorithm automatically save the mean value, standard deviation, and 2D maps for the desired collection of variables (e.g., x-strain, y-strain, shear strain, bad regions, etc.). Select which variables should be saved, and press Ok.
11. When prompted, alter the parameters as desired.
    1. The following values were used in this experiment:
       Surrounding points to calculate strain (numP): 12
       Correlation coefficient for bad region identification (corr_threshold): 0.5
       Subregion size (pixels) for bad region analysis (Subsize): 32
12. When prompted, select the folder that contains the renamed max-intensity z-projections. Note that the software automatically performs incremental ALDIC to determine the strain fields of the deformed images. That is, each deformed image serves as the new "reference" image for the next deformed image. This improves the accuracy of the results (Supplementary Figure 2) compared to performing cumulative ALDIC, where each deformed image is compared back to the original (0% strain) reference image. To perform a cumulative analysis, load the images but only select the original reference image and the deformed image of interest.
    NOTE: The normal strain is calculated as λ - 1, where λ is the tissue stretch. The tissue stretch is calculated according to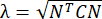 , where N = [1 0]^T or [0 1]^T for the x-direction and y-direction, respectively, and C = F^T F, where F is the deformation gradient calculated using "numP" points surrounding each data point output by the ALDIC algorithm. The shear strain is calculated as 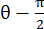, where .
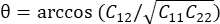13. When prompted, left-click to create a four-point polygon to define the region of interest for measuring the strains. Begin with the point in the top-left corner, and assign the subsequent points in a clockwise manner.
    NOTE: The variable "Storage" saved in the MATLAB workspace contains all the values for the average x-strain, x-strain standard deviation, average y-strain, y-strain standard deviation, average shear strain, shear strain standard deviation, and percentage of bad regions. The bad regions are defined according to the correlation coefficient analysis within the region of interest selected in step 6.13. The folder "NuclearTrackingResults" (which can be renamed by adjusting lines 555 and 556) stores all the plots specified in step 6.10. This folder also contains a spreadsheet file with the name "Results", which stores all the means and standard deviations specified in step 6.10.

Results

Prior to analyzing the strain fields in actual tissue samples, the ALDIC protocol was first validated using digitally strained/transformed images of nuclei within mouse Achilles tendons. Specifically, the images were transformed to digitally produce uniform strains in the x-direction of 2%, 4%, 6%, 8%, and 10% strain with a simulated Poisson's ratio of 1^15,16. The accuracy of the ALDIC algorithm was then assessed by comparing the mean calculated strain values...

Discussion

The objective of this paper was to provide an open-source, validated method to measure the 2D strain fields in tendons under tensile load. The foundation of the software was based on a publicly available ALDIC algorithm¹². This algorithm was embedded into a larger MATLAB code with the added functionality of incremental (versus cumulative) strain analysis. This adapted algorithm was then applied to the tensile testing of tendons, and its accuracy was assessed by two different techniques (i.e., digi...

Materials

Name	Company	Catalog Number	Comments
5-DTAF (5-(4,6-Dichlorotriazinyl) Aminofluorescein), single isomer	ThermoFisher	D16
Calipers	Mitutoyo	500-196-30
Confocal Microscope	Nikon	A1R HD
Corning LSE Vortex Mixer	Coning	6775
DRAQ5 Fluorescent Probe Solution (5 mM)	ThermoFisher	62554
MATLAB	MathWorks	R2022b
Tensile Loading Device	N/A	N/A	Tensile loading device described in Peterson et al, 2020. (ref 13)
Tube Revolver Rotator	ThermoFisher	88881001