A subscription to JoVE is required to view this content. Sign in or start your free trial.
Method Article
פיתוח מודל תוספת קבועה של אזור בזלית של עץ יחיד באמצעות גישה ליניארית של אפקטים מעורבים
In This Article
Summary
מודלים של אפקטים מעורבים הם כלים גמישים ושימושיים לניתוח נתונים עם מבנה סטוכסטי היררכי ביערנות ויכולים לשמש גם לשיפור משמעותי בביצועים של מודלים לצמיחת יער. כאן מוצג פרוטוקול המסונתז מידע הקשור למודלים של אפקטים מעורבים ליניאריים.
Abstract
כאן, פיתחנו מודל של עץ יחיד של מרווחי שטח בסיסיים ל-5 שנים המבוססים על ערכת נתונים הכוללת עצי אספרטה של Picea משנת 21898 מ-779 חלקות לדוגמה הממוקמות במחוז שינג'יאנג, צפון-מערב סין. כדי למנוע מתאמים גבוהים בין תצפיות מאותה יחידת דגימה, פיתחנו את המודל באמצעות גישה ליניארית מעורבת אפקטים עם אפקט עלילה אקראית כדי להסביר את השונות הסטוצ'סטית. משתנים שונים ברמת העצים והמעמד, כגון מדדים לגודל עץ, תחרות ומצב אתר, נכללו כאפקטים קבועים כדי להסביר את השונות השיורית. בנוסף, הטרוסקסטיות וטיפוח אוטומטי תוארו על ידי החדרת פונקציות שונות ומבני תיקון אוטומטי. מודל ההשפעות המעורבות הליניאריות האופטימלי נקבע על ידי מספר סטטיסטיקות התאמה: קריטריון המידע של Akaike, קריטריון המידע הבייסיאני, הסבירות לוגריתם ומבחן יחס הסבירות. התוצאות הצביעו על כך שמשתנים משמעותיים של שטח הבסיס של עץ יחיד היו הטרנספורמציה ההופכית של קוטר בגובה השד, שטח הבסיס של עצים הגדולים מעץ הנושא, מספר העצים לדונם וגובהם. יתר על כן, שגיאות במבנה השונות תוכננו בהצלחה רבה על-ידי הפונקציה המעריכית, והתיקון האוטומטי תוקן באופן משמעותי על-ידי מבנה תוקפנות אוטומטית מסדר ראשון (AR(1)). הביצועים של מודל האפקטים המעורבים הליניאריים שופרו באופן משמעותי ביחס לדגם באמצעות רגרסיה רגילה של ריבועים לפחות.
Introduction
בהשוואה למונוקולטורה מיושנת, ניהול יערות מעורבים בגילאים לא אחידים עם מטרות מרובות זכה לאחרונה לתשומת לב מוגברת1,2,3. חיזוי חלופות ניהול שונות הכרחי לגיבוש אסטרטגיות חזקות לניהול יערות, במיוחד עבור יער מורכב שאינו מיושן בין מינים מעורבים4. גידול יער מודלים תשואה שימשו בהרחבה כדי לחזות עץ או לעמוד פיתוח וקציר תחת תוכניות ניהול שונות5,6,7. מודלים של צמיחת יערות ותפוקה מסווגים למודלים של עצים בודדים, דגמי גודל ומודלים של צמיחה שלמים6,7,8. למרבה הצער, מודלים בגודל מעמד ומודלים שלמים אינם מתאימים ליערות מעורבים בגילאים לא אחידים, הדורשים תיאור מפורט יותר כדי לתמוך בתהליך קבלת ההחלטות של ניהול היער. מסיבה זו, מודלים של צמיחת עצים בודדים ומודלים של תשואה קיבלו תשומת לב מוגברת לאורך העשורים האחרונים בגלל יכולתם לבצע תחזיות עבור יער עומד עם מגוון רחב של הרכבים מינים, מבנים, ואסטרטגיות ניהול9,10,11.
רגרסיה רגילה הריבועים הפחותים (OLS) היא השיטה הנפוצה ביותר לפיתוח מודלים לצמיחת עצים בודדים12,13,14,15. ערכות הנתונים עבור מודלים של צמיחת עצים בודדים שנאספו שוב ושוב לאורך זמן קבוע על אותה יחידת דגימה (כלומר, חלקת מדגם או עץ) יש מבנה סטוכסטי היררכי, עם חוסר עצמאות מתאם מרחבי וטמפורלי גבוה בין תצפיות10,16. המבנה הסטוצטי ההיררכי מפר את הנחות היסוד של רגרסיה OLS: כלומר שאריות עצמאיות ונתונים מופצים בדרך כלל עם שונות שווה. לכן, השימוש ברגרסיה OLS מייצר באופן בלתי נמנע הערכות מוטות של השגיאה הסטנדרטית של אומדני הפרמטרים עבור נתונים אלה13,14.
מודלים של אפקטים מעורבים מספקים כלי רב עוצמה לניתוח נתונים עם מבנים מורכבים, כגון נתוני מדידות חוזרות ונשנות, נתונים אורך ונתונים מרובי רמות. מודלים של אפקטים מעורבים מורכבים הן מרכיבים קבועים, המשותפים לאוכלוסיה המלאה והן רכיבים אקראיים, הספציפיים לכל רמת דגימה. בנוסף, מודלים של אפקטים מעורבים לוקחים בחשבון הטרוסקסואליות ותיקון אוטומטי במרחב ובזמן על ידי הגדרת מבנה שונות-שונות-שונות לא אלכסוני מטריצות17,18,19. מסיבה זו, מודלים של אפקטים מעורבים שימשו בהרחבה ביערנות, כגון במודלים בגובה קוטר20,21, דגמיכתר 22,23, מודלים לדילול עצמי24,25, ומודלים צמיחה26,27.
כאן, המטרה העיקרית הייתה לפתח מודל בהפרש קבוע של אזור בזלת של עץ יחיד באמצעות גישה ליניארית של אפקטים מעורבים. אנו מקווים כי הגישה אפקטים מעורבים יכול להיות מיושם באופן נרחב.
Protocol
1. הכנת נתונים
- הכינו נתוני מידול, הכוללים מידע על עץ יחיד (מינים וקוטר בגובה השד בגובה 1.3 מ') ומידע עלילה (שיפוע, היבט וגובה). במחקר זה, הנתונים התקבלו מן 8 (2009) ו 9 (2014) מלאי היער הלאומי הסיני במחוז שינג'יאנג, צפון מערב סין, הכולל 21,898 תצפיות של 779 חלקות מדגם. חלקות מדגם אלה הן בצורת ריבוע עם גודל של 1 Mu (יחידה סינית של שטח שווה ערך 0.067 חה) ומסודרים באופן שיטתי על רשת של 4 ק"מ x 8 ק"מ.
הערה: תוספת נתונים עבור מידול (אזור בסיסי) דורשת לפחות תקופת גידול אחת (כלומר, שתי תצפיות). - חלק את הנתונים באופן אקראי לשתי ערכות נתונים, כאשר 80% מהנתונים מהחלקות לדוגמה המשמשות להתאמת מודל (ערכת נתונים של פיתוח מודל), המורכבת מ- 17,145 תצפיות מ- 623 חלקות מדגם ו- 20% עבור אימות מודל (ערכת נתונים של אימות מודל) המורכבת מ- 4,753 תצפיות מ- 156 התוויות לדוגמה. סטטיסטיקה תיאורית עבור משתני המפתח בהם נעשה שימוש מסופקת בטבלה 1.
הערה: ניתן להשמיט שלב זה של הליך הדוגמנות, וכל הנתונים משמשים לפיתוח מודלים.
| משתנים | התאמת נתונים | נתוני אימות | |||||||
| דקות | מקס | מתכוון | ס.ד. | דקות | מקס | מתכוון | ס.ד. | ||
| DBH1 (ס"מ) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD (ס"מ) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| מזהה (ס"מ) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (עצים/חה) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| תואר ראשון (מ'2/חה) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| אל (ז) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
שולחן 1. סטטיסטיקת סיכום עבור נתוני התאמה ואימות. DBH1: קוטר ראשוני בגובה השד ב 1.3 מטר (DBH), DBH2: DBH נמדד לאחר 5 שנים של צמיחה, QMD: קוטר ממוצע ריבועי, מזהה: תוספת קוטר במשך 5 שנים (DBH2 – DBH 1 ), BAL: השטח הבסיסי שלעציםגדולים יותר מעץ הנושא (עץ הנושא: העץ שחושב מדדי התחרות), NT: מספר העצים לדונם, BA: אזור בסיסי לדונם, EL: גובה, SD: סטיית תקן.
2. פיתוח מודל בסיסי
- עיין בהפניות לזיהוי משתנים המשפיעים על מרווחי שטח בסיסיים של עץ בודד.
- בחר וחישב משתנים בהתבסס על הנתונים. בדרך כלל, תוספת השטח הבסיסית של העץ הבודד מושפעת משלוש קבוצות של משתנים: גודל עץ, תחרות ומצב אתר27,28,29,30.
- שקול אפקטים בגודלעץכגון DBH 1 , ריבוע של DBH1 (
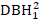 ), הטרנספורמציה ההופכית של DBH1 (1/DBH1), ואת הלוגריתם המשותף של DBH1 (logDBH1) או שילובים שלהם.
), הטרנספורמציה ההופכית של DBH1 (1/DBH1), ואת הלוגריתם המשותף של DBH1 (logDBH1) או שילובים שלהם. - שקול השפעות תחרותיות כגון מדדי תחרות חד-צדדיים ושני צדדיים כדי לכמת באופן מקיף יותר את רמת התחרות שחווה עץ, כמו גם את מעמדו החברתי בתוך הדוכן. תחרות חד-צדדית כוללת את BAL ואת מדד הצפיפות היחסית (RD=DBH1/QMD); תחרות דו-צדדית כוללת את NT ו- BA.
הערה: יש לקחת בחשבון את מדדי התחרות התלויים במרחק אם הנתונים זמינים. - שקול אפקטי אתר כגון היבט (ASP), שיפוע (SL) ו EL. SL ו ASP יש לכלול באמצעות טרנספורמציה של שלב31.
- שקול אפקטים בגודלעץכגון DBH 1 , ריבוע של DBH1 (
- בחר יומן רישום(
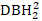 -
- 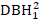 +1) (
+1) ( 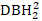 מציין ריבוע של DBH2) כמשתנה התלוי.
מציין ריבוע של DBH2) כמשתנה התלוי. - פתח את המודל הבסיסי בשיטת הרגרסיה החורגת. ודא שהמודל סביר מבחינה ביולוגית ומציג הבדלים משמעותיים בין משתנים בלתי תלויים. השתמש בגורם האינפלציה של השונות (VIF) כדי לבדוק אם יש רב-קולינריות.
- השאר את המשתנים הבלתי תלויים עם p < 0.05 ו- VIF < 5 במודל הבסיסי.
- הפק פלט של תוצאות המודל הבסיסי ושל שאריות ההתוויה. המודל הבסיסי המיוצר כאן משמש בסיס להמשך פיתוח מודל אפקטים מעורבים.
3. פיתוח מודל אפקטים מעורבים ליניארי עם החבילה "nlme" בתוכנת R
- קרא את ערכת הנתונים של פיתוח המודל וטען את החבילה "nlme".
>model.development.dataset=קריאה.csv("E:/DATA/JoVE/מידול.csv",
כותרת=TRUE)
>ספריה(nlme) - בחר התוויות לדוגמה כאפקטים אקראיים כדי לפתח את מודל האפקטים המעורבים.
- התאם את כל השילובים האפשריים של אפקטים אקראיים לשיטת הסבירות המרבית (ML) ופלט את התוצאות.
>דגם<-lme(Y~1/DBH1+BAL+NT+EL,נתונים=model.development.dataset,
שיטה="ML", אקראי =~1| עלילה)
>סיכום(דגם)- הגדר אקראי =~1 הוא היירוט לפרמטרים אקראיים. שנה את ההצהרות האקראיות עד שכל השילובים יתאימו. לדוגמה, כדי להגדיר 1/DBH1 ו- BAL כפרמטרים אקראיים, הקוד הוא כדלקמן: אקראי =~1/DBH1+BAL-1. בנוסף, בתהליך ההתאמה, הקודים עשויים לדווח על שגיאות עקב אי-שיתוף של הדגם המותאם.
- בחר את המודל הטוב ביותר לפי קריטריון המידע של Akaike (AIC), קריטריון המידע הבייסיאני (BIC), הסבירות לוגריתם (Loglik) ומבחן יחס הסבירות (LRT).
>אנובה(דגם.1, דגם.6)
>אנובה(דגם.6, דגם.23)
>אנובה(דגם.23, דגם.30) - קבע את המבנה של Ri. טפל בהטרוסקסטיות ובעיצוב האוטומטי של Ri32. Ri כתוב כדלקמן:
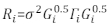 (1)
(1)
כאשר σ 2 הוא גורם קנהמידה לא ידוע השווה לשונות שיורית המודל, Gi היא מטריצה אלכסונית המתארת הטרוסקסטיות, ו- Γi היא מטריצה המתארת תיעול אוטומטי.- שימו לב אם לשיורי ההטרוסקסואליות יש הטרוסקסואליות מהחלקה השיורית. אם קיימת הטרוסקסואליות (לשיורי תבנית או מגמה ברורה), הצג שלוש פונקציות שונות הנמצאות בשימוש תכוף - פונקציית כוח החיבור הקבועה, פונקציית העוצמה והפונקציה המעריכית - כדי ליצור מודל של מבנה השונות של השגיאות.
>דגם.30.1<-lme(Y ~ 1 / DBH1+ BAL + NT + EL,data=model.development.dataset, שיטה="ML",אקראי=~ 1/DBH1+BAL+NT| מגרש
משקולות=varConstPower(טופס=~ מותאם(.)))
>סיכום(דגם.30.1)
>דגם.30.2<-lme(Y ~ 1 / DBH1+ BAL + NT + EL,data=model.development.dataset, שיטה="ML",אקראי=~ 1/DBH1+BAL+NT| מגרש
משקולות=varPower(טופס=~ מותאם(.)))
>סיכום(דגם.30.2)
>דגם.30.3<-lme(Y ~1/DBH1+BAL+NT+EL,data=model.development.dataset, שיטה="ML",אקראי=~1/DBH1+BAL+NT| מגרש
משקולות=varExp(טופס=~ מותאם(.)))
>סיכום(דגם.30.3) - קבע את פונקציית השונות הטובה ביותר עבור המודל בהתאם ל- AIC, BIC, Loglik ו- LRT.
>anova(דגם.30, דגם.30.1)
>אנובה(דגם.30, דגם.30.2)
>אנובה(דגם.30, דגם.30.3) - הצג שלושה מבני תיקון אוטומטי נפוצים - מבנה הסימטריה המורכב (CS), מבנה תוקפנות אוטומטית מסדר ראשון [AR(1)], ושילוב של מבנים ממוצעים רגרסיביים ומרגשים מסדר ראשון [ARMA(1,1)]- כדי להסביר את התיקון האוטומטי.
>דגם.30.3.1<-lme(Y~ 1/DBH1+BAL+NT+EL,נתונים=model.development.dataset, שיטה="ML",
אקראי=~1/DBH1+BAL+NT| עלילה, משקולות=varExp(טופס=~מותאם(.)), corr= corCompSymm())
>סיכום(דגם.30.3.1)
>דגם.30.3.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, שיטה="ML",
אקראי=~1/DBH1+BAL+NT| עלילה,משקולות=varExp(טופס=~ מותאם(.)), corr=corAR1())
>סיכום(דגם.30.3.2)
>דגם.30.3.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, שיטה="ML",
אקראי=~1/DBH1+BAL+NT| עלילה,משקולות=varExp(טופס=~ מותאם(.)), corr=corARMA(q=1,p=1))
>סיכום(דגם.30.3.3) - קבע את מבנה התיקון האוטומטי הטוב ביותר בהתאם ל- AIC, BIC, Loglik ו- LRT.
>אנובה(דגם.30.3, דגם.30.3.2)
הערה: לא ניתן להגדיר את ה- Gi ו- Γi אם אין הטרוסקסואליות ותיקון אוטומטי. - הפק פלט של התוצאות הסופיות של מודל האפקטים המעורבים באמצעות שיטת הסבירות המרבית המוגבלת (REML).
>מעורב.מודל<-lme(Y ~ 1 / DBH1+ BAL + NT + EL, נתונים = model.development.dataset, שיטה ="REML",אקראי =~ 1 /DBH1+BAL+NT| מגרש
משקולות=varExp(טופס=~ מותאם(.)), corr=corAR1())
>סיכום(מעורב.דגם)
- שימו לב אם לשיורי ההטרוסקסואליות יש הטרוסקסואליות מהחלקה השיורית. אם קיימת הטרוסקסואליות (לשיורי תבנית או מגמה ברורה), הצג שלוש פונקציות שונות הנמצאות בשימוש תכוף - פונקציית כוח החיבור הקבועה, פונקציית העוצמה והפונקציה המעריכית - כדי ליצור מודל של מבנה השונות של השגיאות.
4. תיקון הטיה
- שנה את הערכים החזויים של תוספת שטח הבסיס באמצעות המודל הסופי בקנה מידה לוגריתמי לקנה המידה המקורי. עם זאת, שינוי צורה ליניארי כזה של ערך חזוי ממודל שעבר המרת יומן רישום יוצר הטיה משויכת של המרת יומן רישום. כדי להתמודד עם הטיית יומן הרישום, נגזר גורם תיקון ושולב במשוואת החיזוי, המעריכה את ההפרש בפועל של שטח הבסיס החזוי עבור עץ נתון [משוואה (2)]:
 (2)
(2)
כאשר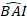 הערך הלוגריתמי החזוי של שטח הבסיס גדל מהמודל, בעוד
הערך הלוגריתמי החזוי של שטח הבסיס גדל מהמודל, בעוד 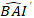 שהערך המומר החזוי של אזור הבסיס גדל σ במשך 5 שנים לאחר תיקון עבור הטיית טרנספורמציה של
שהערך המומר החזוי של אזור הבסיס גדל σ במשך 5 שנים לאחר תיקון עבור הטיית טרנספורמציה של 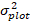 יומן.
יומן. - המר תוספת שטח בסיס (
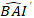 ) למרווח הקוטר.
) למרווח הקוטר.
5. חיזוי והערכה של מודלים
- הכן את ערכת הנתונים של אימות המודל שהופקה בסעיף 1.2 לחיזוי.
- השתמש במודל האפקטים המעורבים הליניאריים כדי לחזות תוספת קבועה של אזור בסיס של עץ בודד. הרכיבים האקראיים חושבו באמצעות מנבא הליניארי הבלתי משוחד הבא:
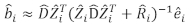 (3)
(3)
כאשר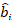 היא וקטור לרכיבים האקראיים;
היא וקטור לרכיבים האקראיים; 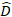 היא מטריצת השונות-covariance עבור שונות בין התוויות;
היא מטריצת השונות-covariance עבור שונות בין התוויות; 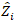 היא מטריצת העיצוב של הרכיבים האקראיים הפועלים בתצפיות המשלימות; היא
היא מטריצת העיצוב של הרכיבים האקראיים הפועלים בתצפיות המשלימות; היא 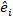 הווקטור השיורי שמרכיביו ניתנים על ידי ההבדל בין מרווחי אזור הבסיס לבין הגדלים החזויים באמצעות מודל האפקטים הקבועים.
הווקטור השיורי שמרכיביו ניתנים על ידי ההבדל בין מרווחי אזור הבסיס לבין הגדלים החזויים באמצעות מודל האפקטים הקבועים. - להעריך ולהשוות את יכולת החיזוי של המודל הבסיסי ואת מודל ההשפעות המעורבות הליניאריות באמצעות שלושת האינדיקטורים הסטטיסטיים הבאים23,33.
 (4)
(4)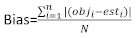 (5)
(5)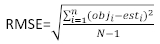 (6)
(6)
כאשר obji הוא תוספת אזור הבסיס, esti הוא במרווחי אזור הבסיס החזויים,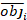 הוא ממוצע התצפיות, ו- N הוא מספר התצפיות.
הוא ממוצע התצפיות, ו- N הוא מספר התצפיות.
תוצאות
מודל ההפרש הקבוע הבסיסי של אזור הבסיס עבור P. אספרטה הובע כמשוואה (7). הערכות הפרמטרים, שגיאות התקן המתאימות שלהן וסטטיסטיקת חוסר ההתאמה מוצגות בטבלה 2. העלילה שיורית מוצגת באיור 1. נצפתה הטרוסקסואליות בולטת של שאריות השיוריות.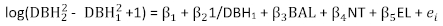 (7)
(7)
Discussion
נושא מכריע לפיתוח מודלים של אפקטים מעורבים היא לקבוע אילו פרמטרים ניתן להתייחס כמו אפקטים אקראיים ואשר צריך להיחשב אפקטים קבועים34,35. הוצעו שתי שיטות. הגישה הנפוצה ביותר היא להתייחס לכל הפרמטרים כאל אפקטים אקראיים ולאחר מכן לבחור את המודל הטוב ביותר על-ידי A...
Disclosures
למחברים אין מה לחשוף.
Acknowledgements
מחקר זה מומן על ידי קרנות המחקר הבסיסיות לאוניברסיטאות המרכזיות, מענק מספר 2019GJZL04. אנו מודים לפרופסור וישנג זנג באקדמיה למלאי ותכנון יערות, מינהל היערנות הלאומי וארץ העשב, סין על מתן גישה לנתונים.
Materials
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
References
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. . Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. . Modeling Forest Trees and Stands. , (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. . Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , (2007).
- Calama, R., Montero, G. . Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257 (2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved