Atomic Force Microscopy Cantilever-Based Nanoindentation: Mechanical Property Measurements at the Nanoscale in Air and Fluid

Resumen

La cuantificación del área de contacto y la fuerza aplicada por la punta de una sonda de microscopio de fuerza atómica (AFM) a una superficie de muestra permite la determinación de propiedades mecánicas a nanoescala. Se discuten las mejores prácticas para implementar la nanoindentación basada en voladizo AFM en aire o fluido en muestras blandas y duras para medir el módulo elástico u otras propiedades nanomecánicas.

Resumen

Un microscopio de fuerza atómica (AFM) mide fundamentalmente la interacción entre la punta de una sonda AFM a nanoescala y la superficie de la muestra. Si se puede cuantificar la fuerza aplicada por la punta de la sonda y su área de contacto con la muestra, es posible determinar las propiedades mecánicas a nanoescala (por ejemplo, elástico o módulo de Young) de la superficie que se está sondeando. Aquí se proporciona un procedimiento detallado para realizar experimentos cuantitativos de nanoindentación basados en voladizo AFM, con ejemplos representativos de cómo se puede aplicar la técnica para determinar los módulos elásticos de una amplia variedad de tipos de muestras, que van desde kPa hasta GPa. Estos incluyen células madre mesenquimales vivas (MSC) y núcleos en tampón fisiológico, secciones transversales de pino loblolly deshidratado incrustado en resina y esquistos Bakken de composición variable.

Además, la nanoindentación basada en voladizo AFM se utiliza para probar la resistencia a la ruptura (es decir, la fuerza de ruptura) de las bicapas de fosfolípidos. Se discuten consideraciones prácticas importantes como la elección y el desarrollo del método, la selección y calibración de la sonda, la identificación de la región de interés, la heterogeneidad de la muestra, el tamaño de la característica y la relación de aspecto, el desgaste de la punta, la rugosidad de la superficie y el análisis de datos y las estadísticas de medición para ayudar a la implementación adecuada de la técnica. Finalmente, se demuestra la colocalización de mapas nanomecánicos derivados de AFM con técnicas de microscopía electrónica que proporcionan información adicional sobre la composición elemental.

Introducción

Comprender las propiedades mecánicas de los materiales es una de las tareas más fundamentales y esenciales en ingeniería. Para el análisis de las propiedades de los materiales a granel, existen numerosos métodos disponibles para caracterizar las propiedades mecánicas de los sistemas de materiales, incluidas las pruebas de tracción¹, las pruebas de compresión² y las pruebas de flexión (flexión) de tres o cuatro puntos³. Si bien estas pruebas a microescala pueden proporcionar información invaluable sobre las propiedades del material a granel, generalmente se realizan hasta el fracaso y, por lo tanto, son destructivas. Además, carecen de la resolución espacial necesaria para investigar con precisión las propiedades a micro y nanoescala de muchos sistemas de materiales que son de interés hoy en día, como películas delgadas, materiales biológicos y nanocompuestos. Para comenzar a abordar algunos de los problemas con las pruebas mecánicas a gran escala, principalmente su naturaleza destructiva, se adoptaron pruebas de microdureza de la mineralogía. La dureza es una medida de la resistencia de un material a la deformación plástica bajo condiciones específicas. En general, las pruebas de microdureza utilizan una sonda rígida, generalmente hecha de acero endurecido o diamante, para sangrar en un material. La profundidad de indentación resultante y / o el área se pueden usar para determinar la dureza. Se han desarrollado varios métodos, incluyendo la dureza Vickers⁴, Knoop⁵ y Brinell⁶ ; Cada uno proporciona una medida de la dureza del material a microescala, pero bajo diferentes condiciones y definiciones, y como tal solo produce datos que se pueden comparar con las pruebas realizadas en las mismas condiciones.

La nanoindentación instrumentada se desarrolló para mejorar los valores relativos obtenidos a través de los diversos métodos de prueba de microdureza, mejorar la resolución espacial posible para el análisis de propiedades mecánicas y permitir el análisis de películas delgadas. Es importante destacar que, al utilizar el método desarrollado por primera vez por Oliver y Pharr⁷, el elástico o módulo de Young, E, de un material de muestra se puede determinar a través de nanoindentación instrumentada. Además, al emplear una sonda nanoindentadora piramidal de tres lados Berkovich (cuya función ideal del área de punta coincide con la de la sonda piramidal de cuatro lados Vickers)⁸, se puede realizar una comparación directa entre las mediciones de dureza a nanoescala y microescala más tradicionales. Con el crecimiento de la popularidad del AFM, la nanoindentación basada en voladizo AFM también comenzó a recibir atención, particularmente para medir las propiedades mecánicas de materiales más blandos. Como resultado, como se muestra esquemáticamente en la Figura 1, las dos técnicas más comúnmente empleadas hoy en día para interrogar y cuantificar las propiedades mecánicas a nanoescala son la nanoindentación instrumentada (Figura 1A) y la nanoindentación basada en voladizo AFM (Figura 1B)⁹, la última de las cuales es el foco de este trabajo.

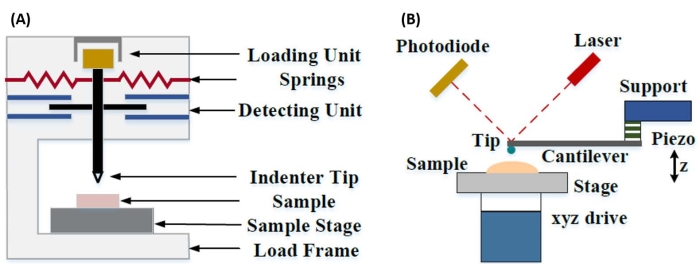
Figura 1: Comparación de sistemas de nanoindentación instrumentados y basados en voladizo AFM. Diagramas esquemáticos que representan sistemas típicos para realizar (A) nanoindentación instrumentada y (B) nanoindentación basada en voladizo AFM. Esta figura fue modificada de Qian et ^al.51. Abreviatura: AFM = microscopía de fuerza atómica. Haga clic aquí para ver una versión más grande de esta figura.

Tanto la nanoindentación instrumentada como la basada en voladizo AFM emplean una sonda rígida para deformar una superficie de muestra de interés y monitorear la fuerza y el desplazamiento resultantes en función del tiempo. Normalmente, el perfil de desplazamiento de carga deseado (es decir, fuerza) o (Z-piezo) es especificado por el usuario a través de la interfaz del software y controlado directamente por el instrumento, mientras que el otro parámetro se mide. La propiedad mecánica que se obtiene con mayor frecuencia de los experimentos de nanoindentación es el módulo elástico (E), también conocido como módulo de Young, que tiene unidades de presión. El módulo elástico de un material es una propiedad fundamental relacionada con la rigidez de enlace y se define como la relación entre la tensión de tracción o compresión (σ, la fuerza aplicada por unidad de área) y la deformación axial (ε, la deformación proporcional a lo largo del eje de indentación) durante la deformación elástica (es decir, reversible o temporal) antes del inicio de la deformación plástica (ecuación 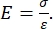[1]):

(1)

Cabe señalar que, debido a que muchos materiales (especialmente los tejidos biológicos) son de hecho viscoelásticos, en realidad, el módulo (dinámico o complejo) consiste en componentes elásticos (almacenamiento, en fase) y viscosos (pérdida, fuera de fase). En la práctica real, lo que se mide en un experimento de nanoindentación es el módulo reducido, E *, que está relacionado con el verdadero módulo de interés de la muestra, E, como se muestra en la ecuación 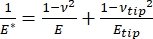(2):

(2)

Donde la punta E y la punta ν son el módulo elástico y la relación de Poisson, respectivamente, de la _punta nanopenetradora, y ν es la relación de Poisson estimada de la muestra. La relación de Poisson es la relación negativa de la deformación transversal a axial, y por lo tanto indica el grado de elongación transversal de una muestra al ser sometida a deformación axial (por ejemplo, durante la carga de nanoindentación), como se muestra en la ecuación 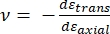(3):

(3)

La conversión de módulo reducido a módulo real es necesaria porque a) parte de la deformación axial impartida por la punta del penetrador puede convertirse en deformación transversal (es decir, la muestra puede deformarse por expansión o contracción perpendicular a la dirección de carga), y b) la punta del penetrador no es infinitamente dura y, por lo tanto, el acto de sangrar la muestra da como resultado una (pequeña) cantidad de deformación de la punta. Tenga en cuenta que en el caso de que la punta E >> E (es decir, la _punta penetradora es mucho más dura que la muestra, lo que a menudo es cierto cuando se usa una sonda de diamante), la relación entre el módulo de muestra reducido y real se simplifica enormemente a E ≈ E * (1 - v²). Mientras que la nanoindentación instrumentada es superior en términos de caracterización precisa de la fuerza y rango dinámico, la nanoindentación basada en voladizo AFM es más rápida, proporciona órdenes de magnitud mayor fuerza y sensibilidad al desplazamiento, permite imágenes de mayor resolución y una mejor localización de la sangría, y puede sondear simultáneamente las propiedades magnéticas y eléctricas a nanoescala⁹. En particular, la nanoindentación basada en voladizo AFM es superior para la cuantificación de propiedades mecánicas a nanoescala de materiales blandos (por ejemplo, polímeros, geles, bicapas lipídicas y células u otros materiales biológicos), películas extremadamente delgadas (sub-μm) (donde los efectos de sustrato pueden entrar en juego dependiendo de la profundidad de indentación)^10,11, y materiales bidimensionales suspendidos (2D)^12,13,14 como el grafeno ^15,16, mica¹⁷, nitruro de boro hexagonal (h-BN)18, o dicalcogenuros de metales de transición (TMDC; por ejemplo, MoS₂)¹⁹. Esto se debe a su exquisita sensibilidad de fuerza (sub-nN) y desplazamiento (sub-nm), que es importante para determinar con precisión el punto de contacto inicial y permanecer dentro de la región de deformación elástica.

En la nanoindentación basada en voladizo AFM, el desplazamiento de una sonda AFM hacia la superficie de la muestra es accionado por un elemento piezoeléctrico calibrado (Figura 1B), con el voladizo flexible eventualmente doblado debido a la fuerza resistiva experimentada al contacto con la superficie de la muestra. Esta flexión o desviación del voladizo generalmente se monitorea reflejando un láser desde la parte posterior del voladizo y en un fotodetector (detector sensible a la posición [PSD]). Junto con el conocimiento de la rigidez en voladizo (en nN/nm) y la sensibilidad a la deflexión (en nm/V), es posible convertir esta deflexión en voladizo medida (en V) en la fuerza (en nN) aplicada a la muestra. Después del contacto, la diferencia entre el movimiento Z-piezo y la deflexión en voladizo produce la profundidad de indentación de la muestra. Combinado con el conocimiento de la función del área de punta, esto permite calcular el área de contacto punta-muestra. La pendiente de las porciones en contacto de las curvas de fuerza-distancia o fuerza-desplazamiento (F-D) resultantes se puede ajustar utilizando un modelo mecánico de contacto apropiado (consulte la sección Análisis de datos de la discusión) para determinar las propiedades nanomecánicas de la muestra. Si bien la nanoindentación basada en voladizo AFM posee algunas ventajas distintivas sobre la nanoindentación instrumentada como se describió anteriormente, también presenta varios desafíos prácticos de implementación, como la calibración, el desgaste de la punta y el análisis de datos, que se discutirán aquí. Otra desventaja potencial de la nanoindentación basada en voladizo AFM es la suposición de elasticidad lineal, ya que el radio de contacto y las profundidades de hendidura deben ser mucho más pequeñas que el radio del penetrador, lo que puede ser difícil de lograr cuando se trabaja con sondas AFM a nanoescala y / o muestras que exhiben una rugosidad superficial significativa.

Tradicionalmente, la nanoindentación se ha limitado a ubicaciones individuales o pequeños experimentos de indentación de cuadrícula, en los que se selecciona una ubicación deseada (es decir, región de interés [ROI]) y se realiza una sola sangría controlada, múltiples sangrías en una sola ubicación separadas por un tiempo de espera y / o una cuadrícula gruesa de sangrías a una velocidad del orden de Hz. Sin embargo, los avances recientes en AFM permiten la adquisición simultánea de propiedades mecánicas y topografía mediante la utilización de modos de imagen basados en curvas de fuerza de alta velocidad (a los que se refieren varios nombres comerciales según el fabricante del sistema), en los que las curvas de fuerza se realizan a una velocidad de kHz bajo control de carga, con la fuerza máxima de la muestra de punta utilizada como punto de ajuste de imagen. También se han desarrollado métodos de apuntar y disparar, lo que permite la adquisición de una imagen de topografía AFM seguida de una posterior nanoindentación selectiva en puntos de interés dentro de la imagen, lo que permite un control espacial a nanoescala sobre la ubicación de la nanoindentación. Si bien no es el enfoque principal de este trabajo, en los resultados representativos se presentan ejemplos de aplicaciones específicas seleccionadas tanto de imágenes basadas en curvas de fuerza como de nanoindentación basada en voladizos de apuntar y disparar, y se pueden usar junto con el protocolo descrito a continuación si está disponible en la plataforma AFM particular empleada. Específicamente, este trabajo describe un protocolo generalizado para la implementación práctica de la nanoindentación basada en voladizo AFM en cualquier sistema AFM capaz y proporciona cuatro ejemplos de casos de uso (dos en aire, dos en fluido) de la técnica, incluidos resultados representativos y una discusión en profundidad de los matices, desafíos y consideraciones importantes para emplear con éxito la técnica.

Protocolo

NOTA: Debido a la amplia variedad de AFM disponibles comercialmente y la diversidad de tipos de muestras y aplicaciones que existen para la nanoindentación basada en voladizo, el protocolo que sigue está diseñado intencionalmente para ser de naturaleza relativamente general, centrándose en los pasos compartidos necesarios para todos los experimentos de nanoindentación basados en voladizo, independientemente del instrumento o fabricante. Debido a esto, los autores asumen que el lector posee al menos una familiaridad básica con el funcionamiento del instrumento específico elegido para realizar la nanoindentación basada en voladizo. Sin embargo, además del protocolo general descrito a continuación, se incluye como material suplementario un procedimiento operativo estándar (POE) detallado paso a paso específico para el AFM y el software utilizado aquí (consulte la Tabla de materiales), centrado en la nanoindentación de muestras en fluidos basada en voladizo.

1. Preparación de la muestra y configuración del instrumento

1. Prepare la muestra de una manera que minimice tanto la rugosidad de la superficie (idealmente a escala nanométrica, ~ 10 veces menos que la profundidad de hendidura prevista) como la contaminación sin alterar las propiedades mecánicas de las áreas de interés.
2. Seleccione una sonda AFM adecuada para la nanoindentación de la muestra prevista en función del medio (es decir, aire o fluido), el módulo esperado, la topografía de la muestra y los tamaños de características relevantes (consulte las consideraciones de selección de la sonda en la discusión). Cargue la sonda en el soporte de la sonda (consulte Tabla de materiales) y fije el soporte de la sonda al cabezal de exploración AFM.
3. Seleccione un modo de nanoindentación apropiado en el software AFM que permita al usuario controlar rampas individuales (es decir, curvas de fuerza-desplazamiento).
   NOTA: El modo específico diferirá entre los diferentes fabricantes de AFM e instrumentos individuales (consulte el POE proporcionado en el Material complementario para obtener más detalles y un ejemplo específico).
4. Alinee el láser en la parte posterior del voladizo de la sonda, frente a la ubicación de la punta de la sonda y en el PSD.
   NOTA: Consulte el ejemplo de aplicación de células madre mesenquimales para obtener más detalles sobre consideraciones importantes al alinear el láser y realizar nanoindentaciones en fluidos, en particular, evitando desechos flotantes y / o burbujas de aire, que pueden dispersar o refractar el haz. La óptica AFM también puede necesitar ser ajustada para compensar el índice de refracción del fluido y para evitar chocar la sonda al atacar la superficie.
   1. Centra el punto del rayo láser en la parte posterior del voladizo maximizando la suma de voltaje (Figura 2A).
   2. Centrar el punto del rayo láser reflejado en el PSD ajustando las señales de deflexión X e Y (es decir, horizontal y vertical) para que estén lo más cerca posible de cero (Figura 2A), proporcionando así el rango de deflexión máximo detectable para producir un voltaje de salida proporcional a la deflexión en voladizo.
5. Si no está seguro de la topografía de la muestra, la rugosidad de la superficie y/o la densidad de la superficie (en el caso de escamas o partículas), realice un escaneo de topografía AFM antes de cualquier experimento de nanoindentación para confirmar la idoneidad de la muestra, como se describe en el paso 1.1 y la parte de preparación de la muestra de la discusión.

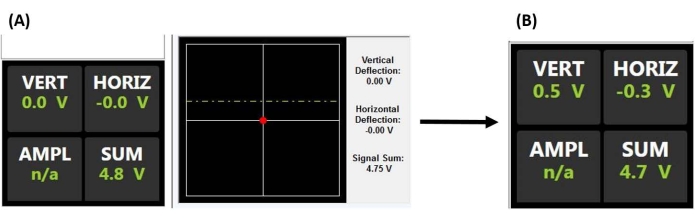
Figura 2: Monitor detector sensible a la posición. (A) Pantalla PSD que indica un láser correctamente alineado que se refleja en la parte posterior del voladizo de la sonda y en el centro de la PSD (como lo demuestra el voltaje de suma grande y la falta de deflexión vertical u horizontal) antes de acoplarse a la superficie de la muestra (es decir, la sonda fuera de contacto con la muestra). (B) El voltaje de deflexión vertical aumenta cuando se desvía el voladizo (por ejemplo, cuando la sonda entra en contacto con la muestra). Abreviaturas: PSD = detector sensible a la posición; VERT = vertical; HORIZ = horizontal; AMPL = amplitud; n/d = no aplicable. Haga clic aquí para ver una versión más grande de esta figura.

2. Calibración de la sonda

NOTA: Se necesitan tres valores para cuantificar las propiedades mecánicas de una muestra utilizando los datos de la curva F-D recopilados durante la nanoindentación basada en voladizo: la sensibilidad a la deflexión (DS ) del sistema en voladizo/PSD (nm/V o V/nm), la constante de resorte en voladizo (nN/nm) y el área de contacto de la sonda, a menudo expresada en términos del radio efectivo de la punta de la sonda (nm) a una profundidad de hendidura dada menor que el radio de la sonda en el caso de una sonda esférica Propina.

1. Calibre el DS del sistema de sonda/AFM mediante rampas sobre un material extremadamente duro (por ejemplo, zafiro, E = 345 GPa) para minimizar la deformación de la muestra y, por lo tanto, el movimiento Z medido del piezo después del inicio del contacto punta-muestra se convierte únicamente en deflexión en voladizo.
   NOTA: La calibración DS debe realizarse en las mismas condiciones que los experimentos de nanoindentación planificados (es decir, temperatura, medio, etc.) para reflejar con precisión el DS del sistema durante los experimentos. Puede ser necesario un período de calentamiento láser largo (30 minutos) para obtener la máxima precisión y permitir que se alcance el equilibrio térmico y se establezca una potencia de salida láser estable y una estabilidad de apuntamiento. El DS debe volver a medirse cada vez que se realinea el láser, incluso si se utiliza la misma sonda, ya que el DS depende de la intensidad y la posición del láser en el voladizo, así como de la calidad de la reflexión de la sonda (es decir, la degradación del revestimiento posterior de la sonda afectará al DS) y la sensibilidad del PSD²⁰.
   1. Configure y realice las sangrías de calibración DS en el zafiro para lograr aproximadamente la misma deflexión de la sonda (en V o nm) que las sangrías de muestra planificadas, ya que el desplazamiento medido es una función del ángulo de deflexión de la punta y se vuelve no lineal para deflexiones grandes.
   2. Determine el DS (en nm/V), o alternativamente, la sensibilidad inversa de la palanca óptica (en V/nm), a partir de la pendiente de la porción lineal del régimen de contacto después del punto de contacto inicial en la curva F-D resultante, como se muestra en la Figura 3A.
   3. Repita la rampa al menos 5 veces, registrando cada valor de DS. Utilice el promedio de los valores para obtener la máxima precisión. Si la desviación estándar relativa (RSD) de las mediciones excede ~1%, vuelva a medir el DS, ya que a veces las primeras curvas F-D no son ideales debido a la introducción inicial de fuerzas adhesivas.
   4. Si la constante de resorte del voladizo de la sonda, k, no está calibrada de fábrica (por ejemplo, mediante vibrometría láser Doppler [LDV]), calibre la constante de resorte.
      NOTA: El método de ajuste térmico es óptimo para voladizos relativamente blandos con k < 10 N/m (consulte la sección de la constante de resorte de la discusión para obtener una lista y descripción de métodos alternativos, particularmente para voladizos rígidos con k > 10 N/m). Como se muestra en la Figura 3B, C, el ajuste térmico generalmente se integra en el software de control AFM.
2. Si la sonda no viene con una medición del radio de la punta calibrada de fábrica (por ejemplo, a través de imágenes de microscopio electrónico de barrido [SEM]), mida el radio efectivo de la punta, R.
   NOTA: Hay dos métodos comunes para medir el radio de la punta (consulte la sección de discusión correspondiente), pero el más común para las puntas de sonda a escala nanométrica es el método de reconstrucción de punta ciega (BTR), que utiliza un estándar de rugosidad (consulte la Tabla de materiales) que contiene numerosas características extremadamente nítidas (sub-nm) que sirven para obtener imágenes efectivas de la punta, en lugar de la punta que obtiene imágenes de la muestra.
   1. Si emplea el método BTR, cree una imagen de la muestra de rugosidad (caracterización de la punta) utilizando una velocidad de escaneo lenta (<0.5 Hz) y altas ganancias de retroalimentación para ayudar a optimizar el seguimiento de las características muy nítidas. Elija un tamaño de imagen y una densidad de píxeles (resolución) en función del radio de punta esperado (por ejemplo, una imagen de 1024 x 1024 píxeles de un área de 3 μm x 3 μm tendrá una resolución lateral de ~ 3 nm).
   2. Utilice el software de análisis de imágenes AFM (consulte la Tabla de materiales) para modelar la punta de la sonda y estimar su radio final y el diámetro efectivo de la punta a la profundidad de indentación de la muestra esperada, como se muestra en la Figura 3D-F.
3. Al completar la calibración de la sonda, introduzca los valores DS, k y R en el software del instrumento, como se muestra en la Figura 4A.
   1. Introduzca una estimación de la relación de Poisson de la muestra, ν, para permitir la conversión del módulo reducido medido al módulo de muestra real⁹. Si se emplea un modelo mecánico de contacto cónico o conisférico basado en la forma de la punta y la profundidad de hendidura, también es necesario introducir el ángulo medio de la punta (Figura 4C).
      NOTA: El módulo es relativamente insensible a pequeños errores o incertidumbres en la relación de Poisson estimada. Una estimación de ν = 0,2-0,3 es un buen punto de partida para muchos materiales²¹.

Figura 3: Calibración de la sonda. (A) Determinación de la sensibilidad a la deflexión. Resultado de una medición representativa de la sensibilidad a la deflexión realizada en un sustrato de zafiro (E = 345 GPa) para una sonda de modo de roscado estándar (k nominal = 42 N/m; ver Tabla de materiales) con un revestimiento de aluminio reflectante en la parte posterior. Se muestran las curvas de aproximación medida (traza azul) y retracción o retirada (traza roja). La sensibilidad de deflexión medida de 59,16 nm/V se determinó ajustando la curva de aproximación entre los puntos de ajuste al contacto y de giro, como lo indica la región entre las líneas rojas punteadas verticales. La región de deflexión negativa evidente en la curva de retracción/retirada antes de arrancar la superficie es indicativa de la adhesión de la punta de la muestra. (B,C) Puesta a punto térmica. Espectros representativos de ruido térmico en voladizo (trazas azules) con ajustes correspondientes (trazas rojas) para dos sondas diferentes. (B) Configuración de ajuste térmico y parámetros de ajuste para una sonda de imagen AFM basada en curva de fuerza estándar (consulte la Tabla de materiales) con su constante de resorte nominal k = 0.4 N / m utilizada como una estimación inicial. El ajuste del espectro de ruido térmico en voladizo produce una frecuencia de resonancia fundamental de f 0 = 79,8 kHz, que está razonablemente bien de acuerdo con el valor nominal de f₀ = 70 kHz. El factor Q medido es 58,1. La bondad del ajuste (R² = 0,99) se basa en la concordancia del ajuste con los datos entre las dos líneas rojas discontinuas verticales. Tenga en cuenta que es importante conocer e introducir tanto la temperatura ambiente como la sensibilidad a la deflexión para obtener resultados precisos. (C) Espectro de ruido térmico en voladizo y ajuste correspondiente (es decir, sintonía térmica) con la constante de resorte calculada resultante k = 0.105 N / m para un voladizo extremadamente blando utilizado para realizar mediciones nanomecánicas en células vivas y núcleos aislados. Tenga en cuenta la frecuencia de resonancia natural significativamente más baja de ~ 2-3 kHz. (D-F) Reconstrucción con punta ciega. Flujo de trabajo representativo de reconstrucción de punta ciega para una sonda de punta de diamante (nominal R = 40 nm; consulte la Tabla de materiales). (D) Una imagen de 5 μm x 5 μm de una muestra de caracterización de punta que consiste en una serie de picos de titanio extremadamente afilados (sub-nm) que sirven para obtener imágenes de la punta de la sonda AFM. (E) Modelo reconstruido resultante (imagen de altura invertida) de la punta de la sonda. (F) Resultados del ajuste de reconstrucción de la punta ciega, incluido un radio final estimado de R = 29 nm y un diámetro efectivo de la punta de 40 nm a una altura seleccionada por el usuario de 8 nm (es decir, profundidad de hendidura << R) desde el vértice de la punta, calculado convirtiendo el área de contacto punta-muestra a esa altura en un diámetro efectivo suponiendo un perfil circular (es decir, A = πr 2 = π(d/2)²) para su uso con modelos mecánicos de contacto esférico. Abreviaturas: AFM = microscopía de fuerza atómica; ETD = diámetro efectivo de la punta. Haga clic aquí para ver una versión más grande de esta figura.

Figura 4: Entradas de interfaz de software. (A) Constantes de calibración de la sonda. Interfaz de usuario de software (consulte Tabla de materiales) para introducir la sensibilidad de deflexión medida, la constante de resorte y el radio de punta para permitir mediciones nanomecánicas cuantitativas. La relación de Poisson tanto de la sonda como de la muestra es necesaria para calcular el elástico o el módulo de Young de la muestra a partir de las curvas de fuerza de nanoindentación basadas en voladizo. (B) Ventana de control de rampa. Interfaz de usuario de software (consulte la Tabla de materiales) para configurar experimentos de nanoindentación basados en voladizo, organizados en los parámetros que describen la rampa en sí (es decir, perfil de hendidura), activación del instrumento (por ejemplo, control de fuerza frente a desplazamiento), análisis de fuerza posterior y límites de movimiento (para mejorar la sensibilidad de medición al reducir el rango sobre el cual el convertidor A / D tiene que operar para controlar el piezo Z y leer la desviación PSD). (C) El ángulo medio de la punta (basado en la geometría de la sonda o la medición directa) es importante si se emplea un modelo mecánico de contacto cónico, piramidal o conisférico (por ejemplo, Sneddon). Haga clic aquí para ver una versión más grande de esta figura.

3. Recopilar datos de desplazamiento de fuerza (F-D)

NOTA: Los valores de los parámetros presentados aquí (consulte la figura 4B) pueden variar según la fuerza y el rango de sangría para una muestra determinada.

1. Navegue por la muestra debajo del encabezado AFM y participe en la región de interés deseada.
   1. Monitoree la señal de deflexión vertical (Figura 2B) o realice una rampa inicial pequeña (~50-200 nm) (Figura 4B) para verificar que la punta y la muestra estén en contacto (consulte la Figura 5A).
   2. Ajuste la posición de la cabeza AFM ligeramente hacia arriba (en pasos correspondientes a ~ 50% del tamaño total de la rampa) y vuelva a rampa. Repita hasta que la punta y la muestra estén fuera de contacto, como lo demuestra una rampa casi plana (Figura 5B) y una desviación vertical mínima del voladizo (Figura 2A).
   3. Una vez que no haya una interacción obvia entre la punta y la muestra (compare la Figura 2A y la Figura 2B), baje el cabezal AFM en una cantidad correspondiente a ~ 50% -100% del tamaño de la rampa para asegurarse de que la punta de la sonda no choque contra la muestra mientras mueve manualmente el cabezal AFM. Rampa de nuevo, repitiendo hasta que se observe una buena curva (Figura 5D) o una curva similar a la Figura 5C. En este último caso, realice un pequeño ajuste adicional de descenso de la cabeza de AFM igual a ~ 20% -50% del tamaño de la rampa para lograr un buen contacto y una curva de fuerza similar a la que se muestra en la Figura 5D.
2. Ajuste los parámetros de la rampa (como se describe a continuación y se muestra en Figura 4B) para optimizar el instrumento, la sonda y la muestra, y obtener rampas similares a las que se muestran en Figura 5D.
   1. Seleccione un tamaño de rampa apropiado (es decir, movimiento total de Z-piezo a través de un ciclo de rampa) dependiendo de la muestra (por ejemplo, espesor, módulo esperado, rugosidad de la superficie) y la profundidad de hendidura deseada.
      NOTA: Para muestras más rígidas, es probable que ocurra menos deformación de la muestra (y, por lo tanto, más deflexión de la sonda para un movimiento piezoeléctrico en Z dado), por lo que el tamaño de la rampa generalmente puede ser más pequeño que para muestras más blandas. Los tamaños de rampa típicos para muestras rígidas y voladizos pueden ser de decenas de nm, mientras que para muestras blandas y voladizos las rampas pueden ser de cientos de nm a unos pocos μm de tamaño; Los ejemplos específicos de aplicaciones seleccionadas se presentan en la sección Resultados representativos. Tenga en cuenta que los tamaños de rampa mínimos y máximos posibles dependen del instrumento.
   2. Seleccione una velocidad de rampa adecuada (1 Hz es un buen punto de partida para la mayoría de las muestras).
      NOTA: La velocidad de rampa puede estar limitada por velocidades / anchos de banda electrónicos de control y / o detección. En combinación con el tamaño de la rampa, la velocidad de rampa determina la velocidad de la punta. La velocidad de la punta es particularmente importante a considerar cuando se sangran materiales blandos donde los efectos viscoelásticos pueden causar artefactos de histéresis ^9,22.
   3. Elija si desea emplear una rampa activada (controlada por carga) o no activada (controlada por desplazamiento).
      NOTA: En una rampa activada, el sistema se acercará a la muestra en pasos definidos por el usuario (según el tamaño y la resolución de la rampa o el número de puntos de datos) hasta que se detecte el umbral de activación deseado (es decir, la fuerza del punto de consigna o la desviación en voladizo), momento en el que el sistema se retraerá a su posición original y mostrará la curva F-D. En una rampa no activada, el sistema simplemente extiende el Z-piezo la distancia especificada por el tamaño de rampa definido por el usuario y muestra la curva F-D medida. Las rampas activadas son preferidas para la mayoría de los casos de uso, pero las rampas no activadas pueden ser útiles cuando se investigan materiales blandos que no exhiben un punto de contacto afilado y fácilmente identificable.
      1. Si se elige una rampa activada , establezca el umbral de activación (fuerza máxima permitida definida por el usuario o deflexión de la rampa) para obtener la hendidura deseada en la muestra.
         NOTA: El uso de un umbral de activación significa que una rampa puede terminar (es decir, la sonda puede comenzar a retraerse) antes de alcanzar el tamaño de rampa completo (extensión Z-piezo) especificado. Los valores pueden variar de unos pocos nN a unos pocos μN, dependiendo del sistema de punta y muestra.
      2. Establezca la posición de la rampa para determinar la parte del rango máximo del Z-piezo que se utilizará para ejecutar la rampa. Asegúrese de que el rango total del tamaño de la rampa no comience o termine fuera del rango máximo de Z-piezo (ver ejemplos representativos en la Figura 6), de lo contrario, una parte de la curva F-D no representará ninguna medida física (es decir, el Z-piezo estará completamente extendido o retraído, no se moverá).
   4. Establezca el número de muestras/rampa (por ejemplo, 512 muestras/ rampa) para lograr la resolución deseada de la medición (es decir, densidad de puntos de la curva F-D).
      NOTA: Las muestras/rampa máximas pueden estar limitadas por restricciones de software (tamaño de archivo) o hardware (por ejemplo, velocidad de conversión de analógico a digital [A/D], dependiendo de la velocidad de rampa). También es posible limitar el rango Z-piezo o de deflexión permitido (consulte los parámetros de límites en la Figura 4B) para aumentar la resolución efectiva del convertidor A/D del sistema.
   5. Ajuste la rotación X para reducir las fuerzas de cizallamiento en la muestra y la punta moviendo simultáneamente la sonda ligeramente en la dirección X (paralela al voladizo) mientras se sangra en la dirección Z (perpendicular al voladizo). Utilice un valor para la rotación X igual al ángulo de desplazamiento del soporte de la sonda en relación con la superficie normal (12° es típico).
      NOTA: El giro X es necesario porque el voladizo está montado en el soporte de la sonda en un ángulo pequeño con respecto a la superficie para permitir que el rayo láser incidente se refleje en el PSD. Además, los ángulos frontal y posterior de la punta de la sonda pueden diferir entre sí (es decir, la punta de la sonda puede ser asimétrica). Se puede obtener información más específica de los fabricantes individuales de sondas y AFM.

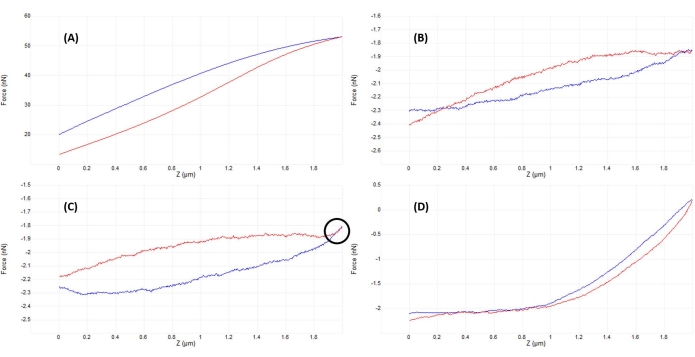
Figura 5: Optimización de la separación punta-muestra después del acoplamiento para obtener buenas curvas de fuerza. Ejemplos secuenciales de curvas representativas de fuerza-desplazamiento obtenidas al sangrar en fluido (solución salina tamponada con fosfato) en un núcleo vivo de células madre mesenquimales con un voladizo de nitruro de silicio blando calibrado ( k nominal = 0.04 N/m) que termina en una punta hemisférica de 5 μm de radio (ver Tabla de materiales). Las curvas se obtuvieron en el proceso de acoplamiento de la superficie celular y la optimización de los parámetros de hendidura, con el enfoque de la sonda mostrada en azul y retracción / retirada en rojo. (A) La punta ya está enganchada y en contacto con la muestra antes de comenzar la rampa, lo que lleva a una gran deflexión y fuerzas en voladizo, sin una línea de base plana de precontacto. (B) Después de mover manualmente la punta lo suficientemente lejos de la muestra, una rampa de 2 μm no activada da como resultado una curva F-D que es casi plana (es decir, prácticamente sin cambio en la fuerza). En condiciones ambientales, la curva sería más plana, pero en fluido, la viscosidad del medio puede causar ligeras deflexiones del voladizo de la sonda durante una rampa como se ve aquí, incluso sin contacto con la superficie. (C) Después de acercarse ligeramente a la superficie antes de comenzar la rampa, las curvas de aproximación y retracción muestran un ligero aumento de la fuerza (aumento de la pendiente) cerca del punto de giro de la rampa (es decir, transición de aproximación a retirada). La señal reveladora a buscar es que las curvas de aproximación (azul) y retirada (rojo) comienzan a superponerse (región indicada por el círculo negro), lo que es indicativo de una interacción física con la superficie. (D) Una curva F-D ideal adquirida después de la optimización de los parámetros de rampa y acercándose ligeramente (~ 1 μm) más cerca de la superficie de la celda que en C para que la sonda pase aproximadamente la mitad de la rampa en contacto con la celda, lo que permite una deformación suficiente para ajustar la parte de contacto de la curva de aproximación y determinar el módulo elástico. La línea de base relativamente larga, plana y de bajo ruido facilita que el algoritmo de ajuste determine el punto de contacto. Abreviatura: F-D = fuerza-desplazamiento. Haga clic aquí para ver una versión más grande de esta figura.

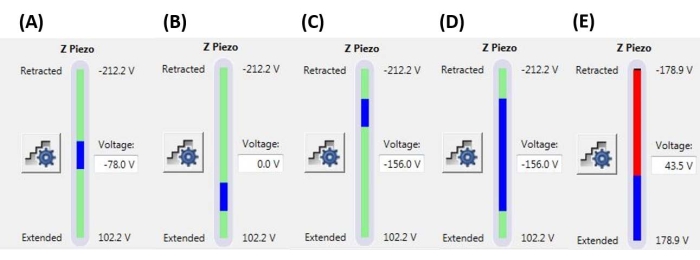
Figura 6: Tamaño y posición de la rampa. Monitor Z-piezo que muestra la extensión de la rampa (barra azul) en relación con el rango total de movimiento Z-piezo disponible (barra verde). (A) La posición piezoeléctrica Z está cerca de la mitad de su rango de movimiento, como lo indica tanto la barra azul que se encuentra aproximadamente en el centro de la barra verde como el voltaje actual Z-piezoeléctrico (-78.0 V) que se encuentra aproximadamente entre sus valores completamente retraídos (-212.2 V) y extendidos (+102.2 V). (B) Z-piezo se extiende con respecto a A, sin voltaje de polarización aplicado. (C) Z-piezo se retrae en relación con A y B. (D) La posición piezoeléctrica Z es la misma que en C a -156.0 V, pero el tamaño de la rampa se ha incrementado en relación con A-C para aprovechar más del rango completo de movimiento del Z-piezo. € El tamaño de la rampa es demasiado grande para la posición actual de la rampa, lo que hace que el Z-piezo se extienda hasta el final de su rango. Esto hará que la curva F-D se aplane ya que el sistema no puede extender el Z-piezo aún más. Abreviatura: F-D = fuerza-desplazamiento. Haga clic aquí para ver una versión más grande de esta figura.

4. Análisis de curva F-D

1. Elija un paquete de software de análisis de datos adecuado. Seleccione y cargue los datos a analizar.
   NOTA: Muchos fabricantes de AFM y programas de software de procesamiento de imágenes AFM tienen soporte incorporado para el análisis de curvas F-D. Alternativamente, la mayor flexibilidad y características de un paquete dedicado de análisis de curvas F-D, como el paquete de software de código abierto AtomicJ, puede ser beneficioso²³, particularmente para el procesamiento por lotes y el análisis estadístico de grandes conjuntos de datos o la implementación de modelos complejos de mecánica de contacto.
2. Valores calibrados de entrada para la constante de resorte, DS y radio de la punta de la sonda, junto con estimaciones del módulo de Young y la relación de Poisson para la punta de la sonda (en función de su composición de material) y la relación de Poisson de la muestra.
   NOTA: Si se utiliza un penetrador de punta de diamante, los valores E tip = 1140 GPa y ν _tip = 0.07 se pueden usar^21,24,25,26. Para una sonda de silicio estándar, normalmente se puede usar la punta E = 170 GPa y la _punta ν = 0.27, aunque el módulo de silicio de Young varía dependiendo de la orientación cristalográfica²⁷.
3. Elija un modelo de mecánica de contacto de nanoindentación apropiado para la punta y la muestra.
   NOTA: Para los muchos modelos comunes de punta esférica (por ejemplo, Hertz, Maugis, DMT, JKR), es imperativo que la profundidad de hendidura en la muestra sea menor que el radio de la punta; de lo contrario, la geometría esférica de la punta de la sonda da paso a una forma cónica o piramidal (Figura 4C). Para modelos cónicos (por ejemplo, Sneddon²⁸) y piramidales, el medio ángulo de la punta (es decir, el ángulo entre la pared lateral de la punta y una línea de bisección perpendicular al extremo de la punta; Figura 4C) debe ser conocido y generalmente está disponible en el fabricante de la sonda. Para obtener más información sobre los modelos de mecánica de contacto, consulte la sección Análisis de datos de thedDiscussion.
4. Ejecute el algoritmo de ajuste. Compruebe el ajuste adecuado de las curvas F-D; un bajo error residual correspondiente a un promedio de R 2 cerca de la unidad (por ejemplo, R² > 0.9) es típicamente indicativo de un buen ajuste al modelo elegido^29,30. Verifique las curvas individuales para inspeccionar visualmente la curva, el ajuste del modelo y los puntos de contacto calculados si lo desea (por ejemplo, consulte la Figura 7 y la sección Análisis de datos de la discusión).

Resultados

Curvas fuerza-desplazamiento
La Figura 7 muestra curvas F-D representativas y casi ideales obtenidas de experimentos de nanoindentación realizados en aire en muestras de pino loblolly incrustadas en resina (Figura 7A) y en fluido (solución salina tamponada con fosfato [PBS]) en núcleos de células madre mesenquimales (MSC) (Figura 7B). El uso de cualquier modelo mecánico de contacto se basa en la determinaci?...

Discusión

Preparación de muestras
Para la nanoindentación en el aire, los métodos de preparación comunes incluyen criosección (por ejemplo, muestras de tejido), esmerilado y / o pulido seguido de ultramicrotoming (por ejemplo, muestras biológicas incrustadas en resina), molienda de iones o preparación de haz de iones enfocado (por ejemplo, muestras de dureza semiconductora, porosa o mixta no susceptibles de pulido), pulido mecánico o electroquímico (por ejemplo, aleaciones metálicas) o deposición de ...

Materiales

Name	Company	Catalog Number	Comments
Atomic force microscope	Bruker	Dimension Icon	Uses Nanoscope control software, including PeakForce Quantitative Nanomechanical Mapping (PF-QNM), FastForce Volume (FFV), and Point-and-Shoot Ramping experimental workspaces
AtomicJ	American Institute of Physics	https://doi.org/10.1063/1.4881683	Flexible, powerful, free open source Java-based force curve analysis software package. Supports numerous contact mechanic models, such as Hertz, Sneddon DMT, JKR, Maugis, and cone or pyramid (including blunt and truncated). Also includes a variety of initial contact point estimation methods to choose from. Supports batch processing of data and subsequent statistical analysis (e.g., averages, standard deviations, histograms, goodness of fit, etc.). Literature citation is: P. Hermanowicz, M. Sarna, K. Burda, and H. Gabry, “AtomicJ: An open source software for analysis of force curves” Rev. Sci. Instrum. 85: 063703 (2014), https://doi.org/10.1063/1.4881683
Buffer solution (PBS)	Fisher Chemical (NaCl), Sigma Aldrich (KCl), Fisher BioReagents (Na2HPO4 and KH2PO4)	S271 (>99% purity NaCl), P9541 (>99% purity KCl), BP332(>99% purity Na2HPO4), BP362 (>99% purity KH2PO4)	Phosphate buffered saline (PBS) was prepared in the laboratory as an aqueous solution consisting of 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.8 mM KH2PO4 dissolved in ultrapure water. Reagents were measured out using an analytical balance, and glassware was cleaned with soap and water followed by autoclaving immediately prior to use.
Chloroform
Diamond tip AFM probe	Bruker	PDNISP	Pre-mounted factory-calibrated cube corner diamond (E = 1140 GPa) tip AFM probe (nominal R = 40 nm) with a stainless steel cantilever (nominal k = 225 N/m, f0 = 50 kHz). Spring constant is measured at the factory (k = 256 N/m for the probe, Serial #13435414, used here) and calibration data (including AFM images of indents showing probe geometry) is provided with the probe.
Diamond ultramicrotome blade	Diatome	Ultra 35°	2.1 mm width. Also used a standard glass blade for intial rough cut of sample surface before transitioning to diamond blade for final surface preparation
Epoxy	Gorilla Glue	26853-31-6	Epoxy resin and hardner were mixed in a 1:1 ratio, a small drop was placed on a stainless steel sample puck (Ted Pella), and V1 grade muscovite mica (Ted Pella) was attached to create an atomically flat surface for preparation of phospholipid membranes.
Ethanol
LR white resin, medium grade (catalyzed)	Electron Microscopy Sciences	14381	500 mL bottle, Lot #150629
Mesenchymal stem cells (MSCs)	N/A	N/A	MSCs for nanomechanical studies were primary cells harvested from 8-10 week old male C57BL/6 mice as described in Goelzer, M. et al. "Lamin A/C Is Dispensable to Mechanical Repression of Adipogenesis" Int J Mol Sci 22: 6580 (2021) doi:10.3390/ijms22126580 and Peister, A. et al. "Adult stem cells from bone marrow (MSCs) isolated from different strains of inbred mice vary in surface epitopes, rates of proliferation, and differentiation potential" Blood 103: 1662-1668 (2004), doi:10.1182/blood-2003-09-3070.
Modulus standards	Bruker	PFQNM-SMPKIT-12M	Used HOPG (E = 18 GPa) and PS (E = 2.7 GPa). Also contains 2x PDMS (Tack 0, E = 2.5 MPa; Tack 4, E = 3.5 MPa), PS-LDPE (E = 2.0/0.2 GPa), fused silica (E = 72.9 GPa), sapphire (E - 345 GPa), and tip characterization (titanium roughness) sample. All samples come pre-mounted on a 12 mm diameter steel disc (sample puck).
Muscovite mica	Ted Pella	50-12	12 mm diameter, V1 grade muscovite mica
Nanscope Analysis	Bruker	Version 2.0	Free AFM image processing and analysis software package, but designed for, and proprietary/limited to Bruker AFMs; similar functionality is available from free, platform-independent AFM image processing and analysis software packages such as Gwyddion, WSxM, and others. Has built-in capabilities for force curve analysis, but AtomicJ is more flexible/full featured (e.g., more built-in contact mechanics models to choose from, statistical analysis of force curve fitting results, etc.) for force curve analysis and handles batch processing of force curves.
Phospholipids: POPC, Cholesterol (ovine)	Avanti Polar Lipids	POPC: CAS # 26853-31-6, Cholesterol: CAS # 57-88-5	POPC lipid dissolved in chloroform (25 mg/mL) was obtained from vendor and used without further purification. Cholesterol powder from the same vendor was dissolved in chloroform (20 mg/mL).
Probe holder (fluid, lipid bilayers)	Bruker	MTFML-V2	Specific to the particular AFM used; MTFML-V2 is a glass probe holder for scanning in fluid on a MultiMode AFM.
Probe holder (fluid, MSCs)	Bruker	FastScan Bio Z-scanner	Used with Dimension FastScan head (XY flexure scanners). Serial number MXYPOM5-1B154.
Probe holder (standard, ambient)	Bruker	DAFMCH	Specific to the particular AFM used; DAFMCH is the standard contact and tapping mode probe holder for the Dimension Icon AFM, suitable for nanoindentation (PF-QNM, FFV, and point-and-shoot ramping)
Sample Puck	Ted Pella	16218	Product number is for 15 mm diameter stainless steel sample puck. Also available in 6 mm, 10 mm, 12 mm, and 20 mm diameters at https://www.tedpella.com/AFM_html/AFM.aspx#anchor842459
Sapphire substrate	Bruker	PFQNM-SMPKIT-12M	Extremely hard surface (E = 345 GPa) for measuring deflection sensitivity of probes (want all of the deflection to come from the probe, not the substrate). Part of the PF-QNM/modulus standards kit.
Scanning electron microscope	Hitachi	S-3400N-II	Located at Boise State. Used to perform co-localized SEM/EDS on all samples except additively manufactured (AM) Ti-6Al-4V.
Silicon AFM probes (standard)	NuNano	Scout 350	Standard tapping mode silicon probe with reflective aluminum backside coating; k = 42 N/m (nominal), f0 = 350 kHz. Nominal R = 5 nm. Also available uncoated or with reflective gold backside coating. Probes with similar specifications are available from other manufacturers (e.g., Bruker TESPA-V2).
Silicon AFM probes (stiff)	Bruker	RTESPA-525, RTESPA-525-30	Rotated tip etched silicon probes with reflective aluminum backside coating; k = 200 N/m (nominal), f0 = 525 kHz. Nominal R = 8 nm for RTESPA-525, R = 30 nm for RTESPA-525-30. Spring constant of each RTESPA-525-30 is measured individually at the factory via laser Doppler vibrometry and supplied with the probe.
Silicon carbide grit paper (abrasive discs)	Allied	50-10005	120 grit
Silicon nitride AFM probes (soft, large radius hemispherical tip)	Bruker	MLCT-SPH-5UM, MLCT-SPH-5UM-DC	Also MLCT-SPH-1UM-DC. New product line of factory-calibrated (probe radius and spring constants of all cantilevers) large radius (R = 1 or 5 mm) hemispherical tip (at the end of a 23 mm long cylindrical shaft) probes. DC = drift compensation coating. 6 cantilevers/probe (A-F). Nominal spring constants: A, k = 0.07 N/m; B, k = 0.02 N/m; C, k = 0.01 N/m; D, k = 0.03 N/m; E, k = 0.1 N/m; F, k = 0.6 N/m.
Silicon nitride AFM probes (soft, medium sharp tip)	Bruker	DNP	4 cantilevers/probe (A-d). Nominal spring constants: A, k = 0.35 N/m; B, k = 0.12 N/m; C, k = 0.24 N/m; D, k = 0.06 N/m. Nominal radii of curvature, R = 10 nm.
Silicon nitride AFM probes (soft, sharp tip)	Bruker	ScanAsyst-Air	Nominal values: resonance frequency, f0 = 70 kHz; spring constant, k = 0.4 N/m; radius of curvature, R = 2 nm. Designed for force curve based AFM imaging.
Superglue	Henkel	Loctite 495	Cyanoacrylate based instant adhesive. Lots of roughly equivalent products are readily available.
Syringe pump	New Era Pump Systems	NE1000US	One channel syringe pump system with infusion and withdrawal capacity
Tip characterization standard	Bruker	PFQNM-SMPKIT-12M	Titanium (Ti) roughness standard. Part of the PF-QNM/modulus standards kit.
Ultrahigh purity nitrogen (UHP N2), 99.999%	Norco	SPG TUHPNI - T	T size compressed gas cylinder of ultrahigh purity (99.999%) nitrogen for drying samples
Ultramicrotome	Leica	EM UC6	Equipped with a glass blade (standard, for intial sample preparation) and a diamond blade (for final preparation)
Ultrapure water	Thermo Fisher	Barnstead Nanopure Model 7146	Model has been discontinued, but equivalent products are available. Produces ≥18.2 MΩ*cm ultrapure water with 1-5 ppb TOC (total organic content), per inline UV monitoring. Includes 0.2 µm particulate filter, ion exchange columns, and UV oxidation chamber.
Variable Speed Grinder	Buehler	EcoMet 3000	Used with silicon carbide grit papers during hand polishing.
Vibration isolation table (active)	Herzan	TS-140	Used with Bruker MultiMode AFM. Sits on a TMC 65-531 vibration isolation table. Bruker Dimension Icon AFM utilizes strictly passive vibration isolation (comes from manufacturer with custom acoustic hood, air table, and granite slab).
Vibration isolation table (passive)	TMC	65-531	35" x 30" vibration isolation table with optional air damping (disabled). Used with Bruker MultiMode AFM. Herzan TS-140 "Table Stable" active vibration control table is located on top.