Rasterkraftmikroskopie Cantilever-basierte Nanoindentation: Messungen mechanischer Eigenschaften auf der Nanoskala in Luft und Flüssigkeit

Zusammenfassung

Die Quantifizierung der Kontaktfläche und der Kraft, die von einer Rasterkraftmikroskop-Sondenspitze (AFM) auf eine Probenoberfläche ausgeübt wird, ermöglicht die Bestimmung der mechanischen Eigenschaften im Nanobereich. Best Practices zur Implementierung von AFM-Cantilever-basierter Nanoindentation in Luft oder Flüssigkeit an weichen und harten Proben zur Messung des Elastizitätsmoduls oder anderer nanomechanischer Eigenschaften werden diskutiert.

Zusammenfassung

Ein Rasterkraftmikroskop (AFM) misst grundlegend die Wechselwirkung zwischen einer nanoskaligen AFM-Sondenspitze und der Probenoberfläche. Wenn die von der Sondenspitze ausgeübte Kraft und ihre Kontaktfläche mit der Probe quantifiziert werden können, ist es möglich, die nanoskaligen mechanischen Eigenschaften (z. B. Elastizität oder Elastizitätsmodul) der zu untersuchenden Oberfläche zu bestimmen. Ein detailliertes Verfahren zur Durchführung quantitativer AFM-Cantilever-basierter Nanoindentationsexperimente wird hier mit repräsentativen Beispielen vorgestellt, wie die Technik zur Bestimmung der Elastizitätsmodule einer Vielzahl von Probentypen, die von kPa bis GPa reichen, angewendet werden kann. Dazu gehören lebende mesenchymale Stammzellen (MSCs) und Zellkerne in physiologischem Puffer, in Harz eingebettete dehydrierte Loblolly-Kiefernquerschnitte und Bakken-Schiefer unterschiedlicher Zusammensetzung.

Darüber hinaus wird die AFM-Cantilever-basierte Nanoindentation verwendet, um die Bruchfestigkeit (d.h. Durchbruchkraft) von Phospholipid-Doppelschichten zu untersuchen. Wichtige praktische Überlegungen wie Methodenwahl und -entwicklung, Sondenauswahl und -kalibrierung, Identifizierung von Regionen von Interesse, Probenheterogenität, Strukturgröße und Aspektverhältnis, Spitzenverschleiß, Oberflächenrauheit sowie Datenanalyse und Messstatistik werden erörtert, um die ordnungsgemäße Implementierung der Technik zu unterstützen. Schließlich wird die Kolokalisierung von AFM-abgeleiteten nanomechanischen Karten mit elektronenmikroskopischen Techniken demonstriert, die zusätzliche Informationen über die Elementzusammensetzung liefern.

Einleitung

Das Verständnis der mechanischen Eigenschaften von Werkstoffen ist eine der grundlegendsten und wesentlichsten Aufgaben im Ingenieurwesen. Für die Analyse von Schüttguteigenschaften stehen zahlreiche Methoden zur Charakterisierung der mechanischen Eigenschaften von Werkstoffsystemen zur Verfügung, darunter Zugversuche¹, Druckversuche² und Drei- oder Vierpunkt-Biegeversuche (Biegeversuche)³. Während diese mikroskaligen Tests unschätzbare Informationen über die Eigenschaften des Schüttguts liefern können, werden sie in der Regel bis zum Versagen durchgeführt und sind daher zerstörerisch. Darüber hinaus fehlt ihnen die räumliche Auflösung, die erforderlich ist, um die mikro- und nanoskaligen Eigenschaften vieler heute interessanter Materialsysteme wie dünner Schichten, biologischer Materialien und Nanokomposite genau zu untersuchen. Um einige der Probleme bei groß angelegten mechanischen Prüfungen, vor allem deren zerstörerische Natur, anzugehen, wurden Mikrohärteprüfungen aus der Mineralogie übernommen. Die Härte ist ein Maß für die Widerstandsfähigkeit eines Materials gegen plastische Verformung unter bestimmten Bedingungen. Im Allgemeinen wird bei Mikrohärteprüfungen eine steife Sonde, die normalerweise aus gehärtetem Stahl oder Diamant besteht, verwendet, um in ein Material einzudrücken. Die resultierende Eindringtiefe und/oder -fläche kann dann zur Bestimmung der Härte verwendet werden. Es wurden mehrere Methoden entwickelt, darunter die Härte Vickers⁴, Knoop⁵ und Brinell⁶ ; Jedes liefert ein Maß für die mikroskalige Materialhärte, jedoch unter unterschiedlichen Bedingungen und Definitionen, und liefert daher nur Daten, die mit Tests verglichen werden können, die unter denselben Bedingungen durchgeführt wurden.

Die instrumentierte Nanoindentation wurde entwickelt, um die relativen Werte zu verbessern, die mit den verschiedenen Mikrohärteprüfmethoden erhalten wurden, die räumliche Auflösung für die Analyse mechanischer Eigenschaften zu verbessern und die Analyse dünner Schichten zu ermöglichen. Wichtig ist, dass durch die Verwendung der zuerst von Oliver und Pharr⁷ entwickelten Methode der Elastizitäts- oder Elastizitätsmodul E eines Probenmaterials durch instrumentierte Nanoindentation bestimmt werden kann. Darüber hinaus kann durch den Einsatz einer dreiseitigen pyramidenförmigen Nanoeindringkörpersonde von Berkovich (deren ideale Spitzenflächenfunktion mit der der vierseitigen Pyramidensonde von Vickers übereinstimmt)⁸ ein direkter Vergleich zwischen nanoskaligen und traditionelleren mikroskaligen Härtemessungen durchgeführt werden. Mit der zunehmenden Popularität des AFM gewann auch die Cantilever-basierte Nanoindentation von AFM an Aufmerksamkeit, insbesondere für die Messung der mechanischen Eigenschaften weicherer Materialien. Wie in Abbildung 1 schematisch dargestellt, sind die beiden heute am häufigsten verwendeten Techniken zur Untersuchung und Quantifizierung nanoskaliger mechanischer Eigenschaften die instrumentierte Nanoindentation (Abbildung 1A) und die AFM-Cantilever-basierte Nanoindentation (Abbildung 1B)⁹, wobei letztere im Mittelpunkt dieser Arbeit steht.

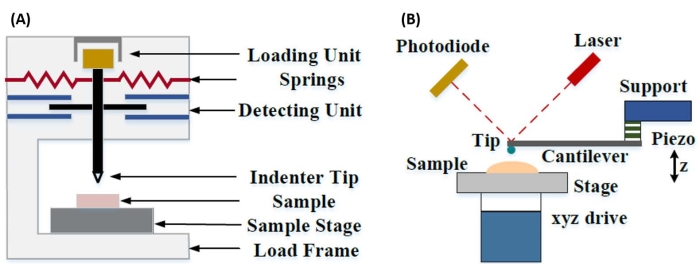
Abbildung 1: Vergleich von instrumentierten und AFM-Cantilever-basierten Nanoindentationssystemen. Schematische Diagramme, die typische Systeme für die Durchführung von (A) instrumentierter Nanoindentation und (B) AFM-Cantilever-basierter Nanoindentation darstellen. Diese Abbildung wurde von Qian et ^al.51 modifiziert. Abkürzung: AFM = Rasterkraftmikroskopie. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

Sowohl instrumentierte als auch AFM-Cantilever-basierte Nanoindentation verwenden eine steife Sonde, um eine zu untersuchende Probenoberfläche zu verformen und die resultierende Kraft und Verschiebung in Abhängigkeit von der Zeit zu überwachen. Typischerweise wird entweder die gewünschte Last (d. h. Kraft) oder das (Z-Piezo-) Wegprofil vom Benutzer über die Softwareschnittstelle vorgegeben und direkt vom Gerät gesteuert, während der andere Parameter gemessen wird. Die mechanische Eigenschaft, die am häufigsten aus Nanoindentationsexperimenten gewonnen wird, ist der Elastizitätsmodul (E), auch als Elastizitätsmodul bezeichnet, der Druckeinheiten hat. Der Elastizitätsmodul eines Materials ist eine grundlegende Eigenschaft, die sich auf die Verbundsteifigkeit bezieht, und ist definiert als das Verhältnis von Zug- oder Druckspannung (σ, die aufgebrachte Kraft pro Flächeneinheit) zur axialen Dehnung (ε, die proportionale Verformung entlang der Eindringachse) während der elastischen (d. h. reversiblen oder vorübergehenden) Verformung vor dem Einsetzen der plastischen Verformung (Gleichung 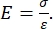[1]):

(1)

Es ist zu beachten, dass, da viele Materialien (insbesondere biologische Gewebe) tatsächlich viskoelastisch sind, der (dynamische oder komplexe) Modul in Wirklichkeit sowohl aus elastischen (Lagerung, in Phase) als auch aus viskosen (Verlust, phasenverschoben) Komponenten besteht. In der Praxis wird in einem Nanoindentationsexperiment der reduzierte Modul E * gemessen, der sich auf den wahren Probenmodul E bezieht, wie in Gleichung (2) gezeigt:

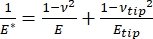(2)

Dabei stehen E-Spitze und ν-Spitze für den Elastizitätsmodul bzw. das Poisson-Verhältnis der Nanoeindringkörperspitze und ν für das geschätzte Poisson-Verhältnis der Probe. Das Poisson-Verhältnis ist das negative Verhältnis der Quer- zur Axialdehnung und gibt somit den Grad der Querdehnung einer Probe an, wenn sie einer axialen Dehnung ausgesetzt wird (z. B. bei einer Nanoindentationsbelastung), wie in Gleichung (3) gezeigt:

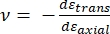(3)

Die Umrechnung vom reduzierten in den tatsächlichen Modul ist notwendig, weil a) ein Teil der axialen Dehnung, die von der Eindringkörperspitze übertragen wird, in Querdehnung umgewandelt werden kann (d. h. die Probe kann sich durch Ausdehnung oder Kontraktion senkrecht zur Belastungsrichtung verformen) und b) die Eindringkörperspitze nicht unendlich hart ist und daher das Eindrücken der Probe zu einer (kleinen) Verformung der Spitze führt. Beachten Sie, dass in dem Fall, in dem die _E-Spitze >> E ist (d. h. die Eindringkörperspitze viel härter ist als die Probe, was bei der Verwendung einer Diamantsonde oft der Fall ist), die Beziehung zwischen dem reduzierten und dem tatsächlichen Probenmodul stark zu E ≈ E*(1 - v²) vereinfacht wird. Während die instrumentierte Nanoindentation in Bezug auf die genaue Kraftcharakterisierung und den Dynamikbereich überlegen ist, ist die Cantilever-basierte Nanoindentation auf AFM-Basis schneller, bietet eine um Größenordnungen höhere Kraft- und Wegempfindlichkeit, ermöglicht eine Bildgebung mit höherer Auflösung und eine verbesserte Lokalisierung von Eindrücken und kann gleichzeitig magnetische und elektrische Eigenschaften im Nanomaßstab untersuchen⁹. Insbesondere die freitragende Nanoindentation auf AFM-Basis eignet sich hervorragend für die Quantifizierung mechanischer Eigenschaften auf der Nanoskala von weichen Materialien (z. B. Polymere, Gele, Lipiddoppelschichten und Zellen oder andere biologische Materialien), extrem dünnen (Sub-μm) Filmen (bei denen Substrateffekte je nach Eindringtiefe ins Spiel kommen können)^10,11 und suspendierten zweidimensionalen (2D) Materialien^12,13,14 wie Graphen ^15,16, Glimmer¹⁷, hexagonales Bornitrid (h-BN)18 oder Übergangsmetalldichalkogenide (TMDCs; z. B. MoS₂)¹⁹. Dies ist auf seine hervorragende Kraft- (sub-nN) und Verschiebungsempfindlichkeit (sub-nm) zurückzuführen, die wichtig ist, um den anfänglichen Kontaktpunkt genau zu bestimmen und innerhalb des elastischen Verformungsbereichs zu bleiben.

Bei der Cantilever-basierten AFM-Nanoindentation wird die Verschiebung einer AFM-Sonde in Richtung der Probenoberfläche durch ein kalibriertes piezoelektrisches Element (Abbildung 1B) betätigt, wobei sich der flexible Cantilever aufgrund der Widerstandskraft, die beim Kontakt mit der Probenoberfläche auftritt, schließlich biegt. Diese Biegung oder Auslenkung des Auslegers wird in der Regel überwacht, indem ein Laser von der Rückseite des Auslegers in einen Photodetektor (positionsempfindlicher Detektor [PSD]) reflektiert wird. Gepaart mit der Kenntnis der Cantilever-Steifigkeit (in nN/nm) und der Durchbiegungsempfindlichkeit (in nm/V) ist es möglich, diese gemessene Cantilever-Auslenkung (in V) in die auf die Probe ausgeübte Kraft (in nN) umzurechnen. Nach dem Kontakt ergibt die Differenz zwischen der Z-Piezobewegung und der Cantilever-Auslenkung die Eindringtiefe der Probe. In Kombination mit der Kenntnis der Spitzenflächenfunktion ermöglicht dies die Berechnung der Spitzen-Probe-Kontaktfläche. Die Steigung der in Kontakt befindlichen Teile der resultierenden Kraft-Weg- oder Kraft-Weg-Kurven (F-D) kann dann mit einem geeigneten Kontaktmechanikmodell (siehe Abschnitt " Datenanalyse" der Diskussion) angepasst werden, um die nanomechanischen Eigenschaften der Probe zu bestimmen. Während die freitragende Nanoindentation auf AFM-Basis einige deutliche Vorteile gegenüber der oben beschriebenen instrumentierten Nanoindentation aufweist, bringt sie auch einige praktische Herausforderungen bei der Implementierung mit sich, wie z. B. Kalibrierung, Spitzenverschleiß und Datenanalyse, die hier diskutiert werden. Ein weiterer potenzieller Nachteil der freitragenden Nanoindentation auf AFM-Basis ist die Annahme einer linearen Elastizität, da der Kontaktradius und die Eindringtiefe viel kleiner sein müssen als der Eindringkörperradius, was bei der Arbeit mit nanoskaligen AFM-Sonden und/oder Proben mit signifikanter Oberflächenrauheit schwierig zu erreichen sein kann.

Traditionell wurde die Nanoindentation auf einzelne Stellen oder kleine Gittereindruckexperimente beschränkt, bei denen eine gewünschte Position (d. h. Region of Interest [ROI]) ausgewählt wird und ein einzelner kontrollierter Eindruck, mehrere Eindrücke an einer einzigen Stelle, die durch eine gewisse Wartezeit getrennt sind, und/oder ein grobes Raster von Einrückungen mit einer Rate in der Größenordnung von Hz durchgeführt werden. Jüngste Fortschritte im AFM ermöglichen jedoch die gleichzeitige Erfassung mechanischer Eigenschaften und Topografie durch die Verwendung von Hochgeschwindigkeits-Kraftkurven-basierten Bildgebungsmodi (je nach Systemhersteller unter verschiedenen Handelsnamen bezeichnet), bei denen Kraftkurven mit einer kHz-Rate unter Lastkontrolle durchgeführt werden, wobei die maximale Kraft zwischen Spitze und Probe als Bildgebungssollwert verwendet wird. Es wurden auch Point-and-Shoot-Methoden entwickelt, die die Aufnahme eines AFM-Topographiebildes mit anschließender selektiver Nanoindentation an interessanten Punkten innerhalb des Bildes ermöglichen, was eine nanoskalige räumliche Kontrolle über die Position der Nanoindentation ermöglicht. Obwohl dies nicht der Hauptfokus dieser Arbeit ist, werden in den repräsentativen Ergebnissen spezifische ausgewählte Anwendungsbeispiele sowohl der kraftkurvenbasierten Bildgebung als auch der Point-and-Shoot-Cantilever-basierten Nanoindentation vorgestellt, die in Verbindung mit dem unten beschriebenen Protokoll verwendet werden können, sofern dies auf der jeweils verwendeten AFM-Plattform verfügbar ist. Konkret skizziert diese Arbeit ein verallgemeinertes Protokoll für die praktische Implementierung der AFM-Cantilever-basierten Nanoindentation auf jedem leistungsfähigen AFM-System und bietet vier Anwendungsfallbeispiele (zwei in Luft, zwei in Flüssigkeit) der Technik, einschließlich repräsentativer Ergebnisse und einer eingehenden Diskussion der Nuancen, Herausforderungen und wichtigen Überlegungen für den erfolgreichen Einsatz der Technik.

Protokoll

HINWEIS: Aufgrund der großen Vielfalt an kommerziell erhältlichen AFMs und der Vielfalt der Probentypen und Anwendungen, die es für die Cantilever-basierte Nanoindentation gibt, ist das folgende Protokoll absichtlich relativ allgemein gehalten und konzentriert sich auf die gemeinsamen Schritte, die für alle Cantilever-basierten Nanoindentationsexperimente unabhängig von Gerät oder Hersteller erforderlich sind. Aus diesem Grund gehen die Autoren davon aus, dass der Leser zumindest über eine grundlegende Vertrautheit mit der Bedienung des spezifischen Instruments verfügt, das für die Durchführung der Cantilever-basierten Nanoindentation ausgewählt wurde. Zusätzlich zu dem unten beschriebenen allgemeinen Protokoll ist jedoch eine detaillierte Schritt-für-Schritt-Standardarbeitsanweisung (SOP) speziell für das AFM und die hier verwendete Software (siehe Materialtabelle), die sich auf die Cantilever-basierte Nanoindentation von Proben in Flüssigkeit konzentriert, als ergänzendes Material enthalten.

1. Probenvorbereitung und Geräteeinrichtung

1. Bereiten Sie die Probe so vor, dass sowohl die Oberflächenrauheit (idealerweise im Nanometerbereich, ~10x weniger als die beabsichtigte Eindringtiefe) und die Verunreinigung minimiert werden, ohne die mechanischen Eigenschaften der interessierenden Bereiche zu verändern.
2. Wählen Sie eine geeignete AFM-Sonde für die Nanoindentation der gewünschten Probe basierend auf dem Medium (d. h. Luft oder Flüssigkeit), dem erwarteten Modul, der Probentopographie und den relevanten Strukturgrößen aus (siehe Überlegungen zur Sondenauswahl in der Diskussion). Setzen Sie die Sonde auf die Sondenhalterung (siehe Materialtabelle) und befestigen Sie die Sondenhalterung am AFM-Scankopf.
3. Wählen Sie in der AFM-Software einen geeigneten Nanoindentationsmodus aus, der dem Benutzer die Kontrolle über einzelne Rampen (d. h. Kraft-Weg-Kurven) ermöglicht.
   HINWEIS: Der spezifische Modus unterscheidet sich je nach AFM-Hersteller und einzelnen Instrumenten (siehe SOP im Zusatzmaterial für weitere Details und ein spezifisches Beispiel).
4. Richten Sie den Laser auf der Rückseite des Sondenauslegers gegenüber der Position der Sondenspitze und in der PSD aus.
   HINWEIS: Im Anwendungsbeispiel für mesenchymale Stammzellen finden Sie weitere Informationen zu wichtigen Überlegungen bei der Ausrichtung des Lasers und der Durchführung von Nanoindentationen in Flüssigkeiten, insbesondere zur Vermeidung von schwebenden Ablagerungen und/oder Luftblasen, die den Strahl streuen oder brechen können. Möglicherweise muss auch die AFM-Optik angepasst werden, um den Brechungsindex der Flüssigkeit zu kompensieren und einen Zusammenstoß der Sonde beim Einrasten in die Oberfläche zu vermeiden.
   1. Zentrieren Sie den Laserstrahlpunkt auf der Rückseite des Cantilevers, indem Sie die Summenspannung maximieren (Abbildung 2A).
   2. Zentrieren Sie den reflektierten Laserstrahlpunkt auf dem PSD, indem Sie die X- und Y-Ablenksignale (d. h. horizontal und vertikal) so einstellen, dass sie so nahe wie möglich an Null liegen (Abbildung 2A), wodurch der maximal erkennbare Ablenkbereich für die Erzeugung einer Ausgangsspannung bereitgestellt wird, die proportional zur Auslenkung des Cantilevers ist.
5. Wenn Sie sich hinsichtlich der Topographie, der Oberflächenrauheit und/oder der Oberflächendichte (im Falle von Flocken oder Partikeln) der Probe nicht sicher sind, führen Sie vor allen Nanoindentationsexperimenten einen AFM-Topographie-Scan durch, um die Eignung der Probe zu bestätigen, wie in Schritt 1.1 und im Probenvorbereitungsteil der Diskussion beschrieben.

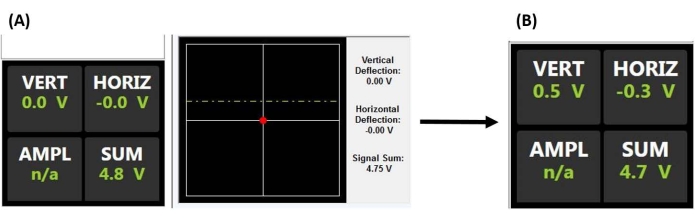
Abbildung 2: Positionsempfindlicher Detektormonitor . (A) PSD-Anzeige, die anzeigt, dass ein korrekt ausgerichteter Laser von der Rückseite des Sonden-Cantilevers auf die Mitte des PSD reflektiert wird (wie durch die große Summenspannung und das Fehlen einer vertikalen oder horizontalen Auslenkung belegt), bevor er auf die Probenoberfläche einrastet (d. h. die Sonde hat keinen Kontakt mit der Probe). (B) Die vertikale Ablenkspannung steigt, wenn der Cantilever ausgelenkt wird (z. B. wenn die Sonde mit der Probe in Kontakt kommt). Abkürzungen: PSD = positionsempfindlicher Detektor; VERT = vertikal; HORIZ = horizontal; AMPL = Amplitude; n/a = nicht zutreffend. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

2. Sonden-Kalibrierung

HINWEIS: Drei Werte sind erforderlich, um die mechanischen Eigenschaften einer Probe anhand der F-D-Kurvendaten zu quantifizieren, die während der Cantilever-basierten Nanoindentation erfasst werden: die Durchbiegungsempfindlichkeit (DS) des Cantilever/PSD-Systems (nm/V oder V/nm), die Cantilever-Federkonstante (nN/nm) und die Sondenkontaktfläche, die häufig als effektiver Sondenspitzenradius (nm) bei einer bestimmten Eindringtiefe ausgedrückt wird, die kleiner ist als der Sondenradius im Falle einer sphärischen Sonde Trinkgeld.

1. Kalibrieren Sie den DS des Sonden-/AFM-Systems durch Rampen auf einem extrem harten Material (z. B. Saphir, E = 345 GPa), so dass die Verformung der Probe minimiert wird und somit die gemessene Z-Bewegung des Piezos nach der Initiierung des Spitzen-Proben-Kontakts ausschließlich in eine Cantilever-Auslenkung umgewandelt wird.
   HINWEIS: Die DS-Kalibrierung muss unter den gleichen Bedingungen wie die geplanten Nanoindentationsexperimente (d. h. Temperatur, Medium usw.) durchgeführt werden, um den DS des Systems während der Experimente genau widerzuspiegeln. Eine lange Aufwärmphase (30 Minuten) des Lasers kann erforderlich sein, um eine maximale Genauigkeit zu erreichen, damit das thermische Gleichgewicht erreicht und eine stabile Laserausgangsleistung und Ausrichtungsstabilität hergestellt werden kann. Der DS muss jedes Mal neu gemessen werden, wenn der Laser neu ausgerichtet wird, auch wenn dieselbe Sonde verwendet wird, da die DS von der Laserintensität und -position auf dem Cantilever sowie von der Qualität der Reflexion von der Sonde (d. h. eine Verschlechterung der Rückseitenbeschichtung der Sonde wirkt sich auf die DS aus) und der Empfindlichkeit des PSD²⁰ abhängt.
   1. Richten Sie die DS-Kalibriereindrücke auf dem Saphir ein und führen Sie sie durch, um ungefähr die gleiche Sondenauslenkung (in V oder nm) wie die geplanten Probeneindrücke zu erreichen, da die gemessene Verschiebung eine Funktion des Ablenkungswinkels der Spitze ist und bei großen Auslenkungen nichtlinear wird.
   2. Bestimmen Sie die DS (in nm/V) oder alternativ die Empfindlichkeit des inversen optischen Hebels (in V/nm) aus der Steigung des linearen Teils des Kontaktbereichs nach dem ersten Kontaktpunkt in der resultierenden F-D-Kurve, wie in Abbildung 3A dargestellt.
   3. Wiederholen Sie die Rampe mindestens 5x und zeichnen Sie jeden DS-Wert auf. Verwenden Sie den Mittelwert der Werte, um eine maximale Genauigkeit zu erzielen. Wenn die relative Standardabweichung (RSD) der Messungen ~1 % überschreitet, messen Sie den DS erneut, da die ersten F-D-Kurven aufgrund der anfänglichen Einführung von Adhäsionskräften manchmal nicht ideal sind.
   4. Wenn die Federkonstante k des Sondencantilevers nicht werkseitig kalibriert ist (z. B. durch Laser-Doppler-Vibrometrie [LDV]), kalibrieren Sie die Federkonstante.
      ANMERKUNG: Die thermische Tune-Methode ist optimal für relativ weiche Ausleger mit k < 10 N/m (siehe den Abschnitt Federkonstante der Diskussion für eine Liste und Beschreibung alternativer Methoden, insbesondere für steife Ausleger mit k > 10 N/m). Wie in Abbildung 3B, C dargestellt, ist die thermische Abstimmung in der Regel in die AFM-Steuerungssoftware integriert.
2. Wenn die Sonde nicht mit einer werkseitig kalibrierten Spitzenradiusmessung ausgestattet ist (z. B. durch Rasterelektronenmikroskop [REM]), messen Sie den effektiven Spitzenradius, R.
   HINWEIS: Es gibt zwei gängige Methoden zur Messung des Spitzenradius (siehe entsprechenden Diskussionsabschnitt), aber die gebräuchlichste für Sondenspitzen im Nanometerbereich ist die BTR-Methode (Blind Tip Reconstruction), bei der ein Rauheitsstandard (siehe Materialtabelle) verwendet wird, der zahlreiche extrem scharfe (Sub-nm) Merkmale enthält, die dazu dienen, die Spitze effektiv abzubilden, anstatt dass die Spitze die Probe abbildet.
   1. Wenn Sie die BTR-Methode verwenden, bilden Sie die Rauheitsprobe (Spitzencharakterisierung) mit einer langsamen Abtastrate (<0,5 Hz) und hohen Rückkopplungsverstärkungen ab, um die Verfolgung der sehr scharfen Merkmale zu optimieren. Wählen Sie eine Bildgröße und Pixeldichte (Auflösung) basierend auf dem erwarteten Spitzenradius (z. B. hat ein 1024 x 1024 Pixel großes Bild eines Bereichs von 3 μm x 3 μm eine laterale Auflösung von ~3 nm).
   2. Verwenden Sie die AFM-Bildanalysesoftware (siehe Materialtabelle), um die Sondenspitze zu modellieren und ihren Endradius und effektiven Spitzendurchmesser bei der erwarteten Probeneindrucktiefe abzuschätzen, wie in Abbildung 3D-F dargestellt.
3. Geben Sie nach Abschluss der Sondenkalibrierung die DS-, k- und R-Werte in die Gerätesoftware ein, wie in Abbildung 4A dargestellt.
   1. Geben Sie eine Schätzung des Poisson-Verhältnisses der Probe, ν, ein, um die Umrechnung des gemessenen reduzierten Moduls in den tatsächlichen Probenmodul⁹ zu ermöglichen. Bei Verwendung eines konischen oder konisphärischen Kontaktmechanikmodells, das auf der Spitzenform und der Eindrucktiefe basiert, ist es auch erforderlich, den Spitzenhalbwinkel einzugeben (Bild 4C).
      ANMERKUNG: Der Modul ist relativ unempfindlich gegenüber kleinen Fehlern oder Unsicherheiten im geschätzten Poisson-Verhältnis. Eine Schätzung von ν = 0,2-0,3 ist ein guter Ausgangspunkt für viele Materialien²¹.

Abbildung 3: Kalibrierung der Sonde. (A) Bestimmung der Ablenkungsempfindlichkeit. Ergebnis einer repräsentativen Messung der Durchbiegungsempfindlichkeit, die an einem Saphirsubstrat (E = 345 GPa) für eine Standard-Abgriffssonde (nominal k = 42 N/m; siehe Materialtabelle) mit einer reflektierenden Aluminiumrückseitenbeschichtung durchgeführt wurde. Dargestellt sind die gemessenen Anfahr- (blaue Kurve) und Ein- bzw. Ausfahrkurven (rote Kurve). Die gemessene Ablenkungsempfindlichkeit von 59,16 nm/V wurde bestimmt, indem die Annäherungskurve zwischen den Kontakt- und Wendepunkten eingepasst wurde, was durch den Bereich zwischen den vertikalen gestrichelten roten Linien angezeigt wird. Der Bereich der negativ gehenden Durchbiegung, der in der Rückzugs-/Rückzugskurve vor dem Abziehen der Oberfläche erkennbar ist, weist auf eine Haftung zwischen Spitze und Probe hin. (B,C) Thermische Abstimmung. Repräsentative freitragende thermische Rauschspektren (blaue Leiterbahnen) mit entsprechenden Passungen (rote Spuren) für zwei verschiedene Sonden. (B) Thermische Abstimmungs- und Anpassungsparameter für eine auf Standardkraftkurve basierende AFM-Bildgebungssonde (siehe Materialtabelle) mit ihrer nominalen Federkonstante k = 0,4 N/m, die als erste Schätzung verwendet wird. Die Anpassung des freitragenden thermischen Rauschspektrums ergibt eine Grundresonanzfrequenz von f 0 = 79,8 kHz, die in einigermaßen guter Übereinstimmung mit dem Nennwert von f₀ = 70 kHz steht. Der gemessene Q-Faktor beträgt 58,1. Die Anpassungsgüte (R² = 0,99) basiert auf der Übereinstimmung der Anpassung mit den Daten zwischen den beiden vertikalen gestrichelten roten Linien. Beachten Sie, dass es wichtig ist, sowohl die Umgebungstemperatur als auch die Durchbiegungsempfindlichkeit zu kennen und einzugeben, um genaue Ergebnisse zu erzielen. (C) Cantilever-Thermal-Rauschspektrum und entsprechende Anpassung (d. h. thermische Abstimmung) mit resultierender berechneter Federkonstante k = 0,105 N/m für einen extrem weichen Cantilever, der zur Durchführung nanomechanischer Messungen an lebenden Zellen und isolierten Zellkernen verwendet wird. Man beachte die deutlich niedrigere Eigenresonanzfrequenz von ~2-3 kHz. (D-F) Rekonstruktion der Blindspitze. Repräsentativer Arbeitsablauf zur Rekonstruktion von Blindspitzen für eine Diamantspitzensonde (nominal R = 40 nm; siehe Materialtabelle). (D) Ein 5 μm x 5 μm großes Bild einer Spitzencharakterisierungsprobe, bestehend aus einer Reihe von extrem scharfen (Sub-nm) Titan-Spikes, die zur Abbildung der AFM-Sondenspitze dienen. (E) Resultierendes rekonstruiertes Modell (invertiertes Höhenbild) der Sondenspitze. (F) Ergebnisse der Rekonstruktion der Blindspitze, einschließlich eines geschätzten Endradius von R = 29 nm und eines effektiven Spitzendurchmessers von 40 nm bei einer vom Benutzer gewählten Höhe von 8 nm (d. h. Eindringtiefe << R) von der Spitzenspitze, berechnet durch Umrechnung der Kontaktfläche zwischen Spitze und Probe in dieser Höhe in einen effektiven Durchmesser unter Annahme eines kreisförmigen Profils (d. h. A = πr 2 = π(d/2)²) zur Verwendung mit Modellen der Kugelkontaktmechanik. Abkürzungen: AFM = Rasterkraftmikroskopie; ETD = effektiver Spitzendurchmesser. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

Abbildung 4: Eingänge der Softwareschnittstelle. (A) Kalibrierungskonstanten der Sonde. Software-Benutzeroberfläche (siehe Materialtabelle) zur Eingabe der gemessenen Durchbiegungsempfindlichkeit, der Federkonstante und des Spitzenradius, um quantitative nanomechanische Messungen zu ermöglichen. Das Poisson-Verhältnis von Sonde und Probe ist notwendig, um die Elastizität oder den Elastizitätsmodul der Probe aus den Cantilever-basierten Nanoindentationskraftkurven zu berechnen. (B) Fenster zur Steuerung der Rampe. Software-Benutzeroberfläche (siehe Materialtabelle) zum Einrichten von Cantilever-basierten Nanoindentationsexperimenten, unterteilt in die Parameter, die die Rampe selbst beschreiben (d. h. das Eindringprofil), die Geräteauslösung (z. B. Kraft-Weg-Steuerung), die anschließende Kraftanalyse und die Bewegungsgrenzen (zur Verbesserung der Messempfindlichkeit durch Verengung des Bereichs, über den der A/D-Wandler bei der Steuerung des Z-Piezos und dem Ablesen der PSD-Auslenkung arbeiten muss). (C) Der Halbwinkel der Spitze (basierend auf der Sondengeometrie oder der direkten Messung) ist wichtig, wenn ein konisches, pyramidales oder konisphärisches Modell der Kontaktmechanik (z. B. Sneddon) verwendet wird. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

3. Erfassen von Kraft-Weg-Daten (F-D)

HINWEIS: Die hier dargestellten Parameterwerte (siehe Abbildung 4B) können je nach Kraft und Eindringbereich für eine bestimmte Probe variieren.

1. Navigieren Sie durch die Probe unter dem AFM-Kopf und greifen Sie auf den gewünschten Bereich von Interesse ein.
   1. Überwachen Sie das vertikale Ablenksignal (Abbildung 2B) oder führen Sie eine kleine (~50-200 nm) Anfangsrampe (Abbildung 4B) durch, um zu überprüfen, ob die Spitze und die Probe in Kontakt sind (siehe Abbildung 5A).
   2. Passen Sie die Position des AFM-Kopfes leicht nach oben an (in Schritten, die ~50% der vollen Rampengröße entsprechen) und fahren Sie erneut. Wiederholen Sie den Vorgang, bis die Spitze und die Probe keinen Kontakt mehr haben, was durch eine nahezu flache Rampe (Abbildung 5B) und eine minimale vertikale Auslenkung des Cantilevers (Abbildung 2A) belegt wird.
   3. Sobald keine offensichtliche Wechselwirkung zwischen Spitze und Probe vorhanden ist (vgl. Abbildung 2A und Abbildung 2B), senken Sie den AFM-Kopf um einen Betrag ab, der ~50 % bis 100 % der Rampengröße entspricht, um sicherzustellen, dass die Sondenspitze beim manuellen Bewegen des AFM-Kopfes nicht gegen die Probe stößt. Wiederholen Sie den Vorgang erneut, bis entweder eine gute Kurve (Abbildung 5D) oder eine Kurve ähnlich wie in Abbildung 5C beobachtet wird. Führen Sie im letzteren Fall eine zusätzliche kleine AFM-Kopfabsenkungseinstellung durch, die ~20%-50% der Rampengröße entspricht, um einen guten Kontakt und eine Kraftkurve ähnlich der in Abbildung 5D gezeigten zu erreichen.
2. Passen Sie die Rampenparameter an (wie unten beschrieben und in Abbildung 4B), um für das Instrument, die Sonde und die Probe zu optimieren und Rampen zu erhalten, die den in Abbildung 5D.
   1. Wählen Sie eine geeignete Rampengröße (d. h. die gesamte Z-Piezo-Bewegung während eines Rampenzyklus) in Abhängigkeit von der Probe (z. B. Dicke, erwarteter Modul, Oberflächenrauheit) und der gewünschten Eindringtiefe.
      HINWEIS: Bei steiferen Proben ist es wahrscheinlich, dass eine geringere Probenverformung (und damit eine größere Sondenauslenkung bei einer bestimmten Z-Piezo-Bewegung) auftritt, sodass die Rampengröße im Allgemeinen kleiner sein kann als bei weicheren Proben. Typische Rampengrößen für steife Proben und Cantilever können Dutzende von nm betragen, während Rampen für weiche Proben und Cantilever Hunderte von nm bis zu einigen μm groß sein können. Ausgewählte Anwendungsbeispiele werden in der Rubrik Repräsentative Ergebnisse vorgestellt. Beachten Sie, dass die minimal und maximal möglichen Rampengrößen instrumentenabhängig sind.
   2. Wählen Sie eine geeignete Rampenrate (1 Hz ist ein guter Ausgangspunkt für die meisten Samples).
      HINWEIS: Die Rampenrate kann durch elektronische Geschwindigkeiten/Bandbreiten der Steuerung und/oder Erkennung begrenzt werden. In Kombination mit der Rampengröße bestimmt die Rampenrate die Spitzengeschwindigkeit. Die Spitzengeschwindigkeit ist besonders wichtig beim Eindrücken weicher Materialien, bei denen viskoelastische Effekte Hystereseartefakte verursachen können ^9,22.
   3. Wählen Sie, ob eine ausgelöste (lastgesteuerte) oder nicht ausgelöste (verlagerungsgesteuerte) Rampe verwendet werden soll.
      HINWEIS: Bei einer getriggerten Rampe nähert sich das System der Probe in benutzerdefinierten Schritten (basierend auf der Rampengröße und -auflösung oder der Anzahl der Datenpunkte), bis die gewünschte Auslöseschwelle (d. h. die Sollwertkraft oder die Cantilever-Auslenkung) erkannt wird, woraufhin sich das System in seine ursprüngliche Position zurückzieht und die F-D-Kurve anzeigt. Bei einer ungetriggerten Rampe verlängert das System den Z-Piezo einfach um den durch die benutzerdefinierte Rampengröße vorgegebenen Abstand und zeigt die gemessene F-D-Kurve an. Getriggerte Rampen werden für die meisten Anwendungsfälle bevorzugt, aber nicht getriggerte Rampen können nützlich sein, wenn weiche Materialien untersucht werden, die keinen scharfen, leicht identifizierbaren Kontaktpunkt aufweisen.
      1. Wenn eine getriggerte Rampe gewählt wird, legen Sie den Trigger-Schwellenwert (benutzerdefinierte maximal zulässige Kraft oder Auslenkung der Rampe) so fest, dass die gewünschte Einkerbung in der Probe erzielt wird.
         HINWEIS: Die Verwendung einer Auslöseschwelle bedeutet, dass eine Rampe beendet werden kann (d. h. die Sonde kann beginnen, sich zurückzuziehen), bevor die angegebene volle Rampengröße (Z-Piezo-Verlängerung) erreicht ist. Die Werte können je nach Tip-Sample-System zwischen einigen nN und einigen μN liegen.
      2. Legen Sie die Rampenposition fest, um den Teil des maximalen Bereichs des Z-Piezos zu bestimmen, der zum Ausführen der Rampe verwendet wird. Stellen Sie sicher, dass der Gesamtbereich der Rampengröße nicht außerhalb des maximalen Z-Piezobereichs beginnt oder endet (siehe repräsentative Beispiele in Abbildung 6), da sonst ein Teil der F-D-Kurve keine physikalische Messung darstellt (d. h. der Z-Piezo wird vollständig ausgefahren oder eingefahren und bewegt sich nicht).
   4. Stellen Sie die Anzahl der Samples/Rampe ein (z. B. 512 Samples/ Rampe), um die gewünschte Auflösung der Messung zu erreichen (d. h. Punktdichte der F-D-Kurve).
      HINWEIS: Die maximale Anzahl von Samples/Rampen kann durch Software- (Dateigröße) oder Hardwarebeschränkungen (z. B. Wandlungsgeschwindigkeit von analog zu digital [A/D], abhängig von der Rampenrate) begrenzt sein. Es ist auch möglich, den zulässigen Z-Piezo- oder Ablenkungsbereich zu begrenzen (siehe Grenzwertparameter in Abbildung 4B), um die effektive Auflösung des A/D-Wandlers des Systems zu erhöhen.
   5. Stellen Sie die X-Drehung ein, um die Scherkräfte auf die Probe und die Spitze zu reduzieren, indem Sie die Sonde gleichzeitig leicht in X-Richtung (parallel zum Cantilever) bewegen, während sie in Z-Richtung (senkrecht zum Cantilever) eingedrückt wird. Verwenden Sie einen Wert für die X-Drehung, der dem Versatzwinkel des Sondenhalters relativ zur Oberflächennormalen entspricht (12° ist typisch).
      Anmerkungen: Die X-Drehung ist erforderlich, da der Cantilever in einem kleinen Winkel zur Oberfläche in der Sondenhalterung montiert ist, damit der einfallende Laserstrahl in die PSD reflektiert werden kann. Darüber hinaus können der vordere und hintere Winkel der Sondenspitze voneinander abweichen (d. h. die Sondenspitze kann asymmetrisch sein). Genauere Informationen erhalten Sie bei den einzelnen Sonden- und AFM-Herstellern.

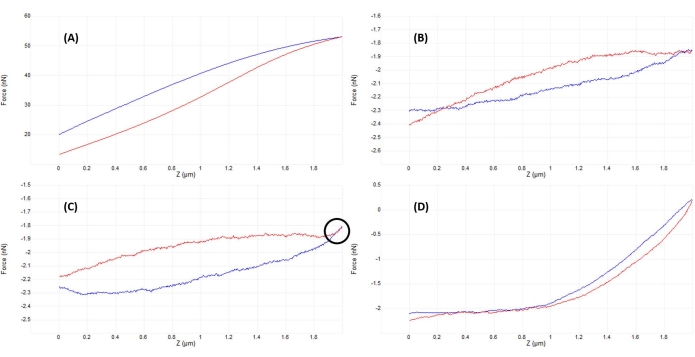
Abbildung 5: Optimierung der Trennung zwischen Spitze und Probe nach dem Einrasten, um gute Kraftkurven zu erhalten. Aufeinanderfolgende Beispiele repräsentativer Kraft-Weg-Kurven, die beim Eindrücken in Flüssigkeit (phosphatgepufferte Kochsalzlösung) auf einem lebenden mesenchymalen Stammzellkern mit einem kalibrierten weichen Siliziumnitrid-Cantilever (nominal k = 0,04 N/m) erhalten wurden, der in einer halbkugelförmigen Spitze mit einem Radius von 5 μm endet (siehe Materialtabelle). Die Kurven wurden während des Eingriffs in die Zelloberfläche und der Optimierung der Injektionsparameter erhalten, wobei der Sondenansatz blau und das Ein- und Ausfahren rot dargestellt wurde. (A) Die Spitze ist bereits vor Beginn der Rampe eingerastet und in Kontakt mit der Probe, was zu einer großen Auslenkung und Kräften des Auslegers führt, ohne dass eine flache Grundlinie vor dem Kontakt vorhanden ist. (B) Nachdem die Spitze manuell ausreichend weit von der Probe entfernt wurde, führt eine nicht ausgelöste 2-μm-Rampe zu einer F-D-Kurve, die nahezu flach ist (d. h. praktisch keine Kraftänderung). Unter Umgebungsbedingungen wäre die Kurve flacher, aber in Flüssigkeiten kann die Viskosität des Mediums während einer Rampe, wie hier zu sehen, zu leichten Auslenkungen des Sondenauslegers führen, auch ohne Oberflächenkontakt. (C) Nach der Annäherung an die Oberfläche vor Beginn der Rampe zeigen die An- und Rückzugskurven eine leichte Kraftzunahme (erhöhte Steigung) in der Nähe des Wendepunkts der Rampe (d. h. Übergang vom Anflug zum Rückzug). Das verräterische Zeichen, auf das man achten sollte, ist, dass sich die Annäherungs- (blau) und Rückzugskurven (rot) zu überlappen beginnen (Bereich durch den schwarzen Kreis gekennzeichnet), was auf eine physikalische Wechselwirkung mit der Oberfläche hinweist. (D) Eine ideale F-D-Kurve, die nach Optimierung der Rampenparameter aufgenommen wurde und sich der Zelloberfläche etwas näher (~1 μm) als in C nähert, so dass die Sonde etwa die Hälfte der Rampe in Kontakt mit der Zelle verbringt, was eine ausreichende Verformung ermöglicht, um den Kontaktteil der Annäherungskurve anzupassen und den Elastizitätsmodul zu bestimmen. Die relativ lange, flache, rauscharme Basislinie erleichtert dem Anpassungsalgorithmus die Bestimmung des Kontaktpunkts. Abkürzung: F-D = Kraft-Weg. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

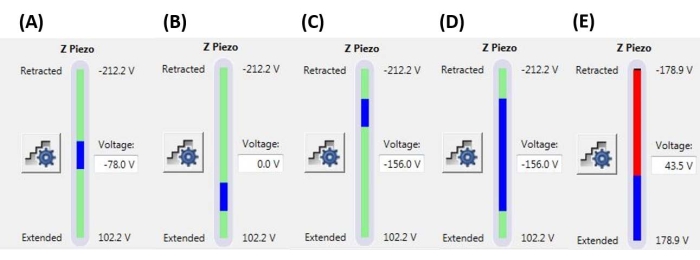
Abbildung 6: Größe und Position der Rampe. Z-Piezo-Monitor, der die Ausdehnung der Rampe (blauer Balken) im Verhältnis zum gesamten verfügbaren Z-Piezo-Bewegungsbereich (grüner Balken) anzeigt. (A) Die Z-Piezo-Position liegt nahe der Mitte seines Bewegungsbereichs, was sowohl dadurch angezeigt wird, dass sich der blaue Balken ungefähr in der Mitte des grünen Balkens befindet, als auch dadurch, dass die aktuelle Z-Piezo-Spannung (-78,0 V) ungefähr zwischen den vollständig eingefahrenen (-212,2 V) und ausgefahren (+102,2 V) Werten liegt. (B) Der Z-Piezo wird relativ zu A erweitert, ohne dass eine Vorspannung angelegt wird. (C) Z-Piezo ist relativ zu A und B eingezogen. (D) Die Z-Piezo-Position ist die gleiche wie in C bei -156,0 V, aber die Rampengröße wurde im Verhältnis zu A-C vergrößert, um den vollen Bewegungsbereich des Z-Piezos besser nutzen zu können. € Die Rampengröße ist zu groß für die aktuelle Rampenposition, was dazu führt, dass der Z-Piezo bis zum Ende seines Bereichs verlängert wird. Dies führt dazu, dass die F-D-Kurve abflacht, da das System den Z-Piezo nicht weiter ausdehnen kann. Abkürzung: F-D = Kraft-Weg. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

4. Analyse der F-D-Kurve

1. Wählen Sie ein geeignetes Softwarepaket für die Datenanalyse. Wählen Sie die zu analysierenden Daten aus und laden Sie sie.
   HINWEIS: Viele AFM-Hersteller und AFM-Bildverarbeitungsprogramme verfügen über eine integrierte Unterstützung für die Analyse von F-D-Kurven. Alternativ können die erhöhte Flexibilität und die Funktionen eines speziellen F-D-Kurvenanalysepakets, wie z. B. das Open-Source-Softwarepaket AtomicJ, von Vorteil sein²³, insbesondere für die Stapelverarbeitung und statistische Analyse großer Datensätze oder die Implementierung komplexer kontaktmechanischer Modelle.
2. Geben Sie kalibrierte Werte für die Federkonstante, DS und den Radius der Sondenspitze ein, zusammen mit Schätzungen des Elastizitätsmoduls und des Poisson-Verhältnisses für die Sondenspitze (basierend auf ihrer Materialzusammensetzung) und des Poisson-Verhältnisses der Probe.
   HINWEIS: Bei Verwendung eines Diamantspitzen-Eindringkörpers können die Werte _E-Spitze = 1140 GPa und ν-Spitze = 0,07 verwendet werden^21,24,25,26. Für eine Standard-Siliziumsonde kann typischerweise eine _E-Spitze = 170 GPa und eine ν-Spitze = 0,27 verwendet werden, obwohl der Elastizitätsmodul des Siliziums in Abhängigkeit von der kristallographischen Ausrichtung²⁷ variiert.
3. Wählen Sie ein Modell mit Nanoindentationskontaktmechanik, das für die Spitze und die Probe geeignet ist.
   HINWEIS: Für die vielen gängigen Modelle mit kugelförmiger Spitze (z. B. Hertz, Maugis, DMT, JKR) ist es zwingend erforderlich, dass die Eindrucktiefe in die Probe kleiner als der Spitzenradius ist. Andernfalls weicht die sphärische Geometrie der Sondenspitze einer konischen oder pyramidenförmigen Form (Abbildung 4C). Bei konischen (z. B. Sneddon²⁸) und pyramidenförmigen Modellen ist der Halbwinkel der Spitze (d. h. der Winkel zwischen der Seitenwand der Spitze und einer halbierenden Linie senkrecht zum Spitzenende; Abbildung 4C) muss bekannt sein und ist in der Regel beim Sondenhersteller erhältlich. Weitere Informationen zu Kontaktmechanikmodellen finden Sie im Abschnitt Datenanalyse von thedDiscussion.
4. Führen Sie den Anpassungsalgorithmus aus. Überprüfen Sie, ob die F-D-Kurven richtig passen. Ein geringer Restfehler, der einem durchschnittlichen R2-Wert nahe Eins entspricht (z. B.^R2 > 0,9), weist in der Regel auf eine gute Anpassung an das gewählte Modell^{hin 29,30}. Überprüfen Sie stichprobenartig einzelne Kurven, um die Kurve, die Modellanpassung und die berechneten Kontaktpunkte bei Bedarf visuell zu überprüfen (siehe z. B. Abbildung 7 und den Abschnitt "Datenanalyse" der Diskussion).

Ergebnisse

Kraft-Weg-Kurven
Abbildung 7 zeigt repräsentative, nahezu ideale F-D-Kurven, die aus Nanoindentationsexperimenten gewonnen wurden, die in Luft an in Harz eingebetteten Loblolly-Kiefernproben (Abbildung 7A) und in Flüssigkeit (phosphatgepufferte Kochsalzlösung [PBS]) an mesenchymalen Stammzellkernen (MSC) (Abbildung 7B) durchgeführt wurden. Die Verwendung eines beliebigen kontaktmechanischen Modells beruht auf...

Diskussion

Probenvorbereitung
Zu den gängigen Präparationsmethoden für die Nanoindentation in Luft gehören Kryoschnitt (z. B. Gewebeproben), Schleifen und/oder Polieren mit anschließendem Ultramikrotomieren (z. B. in Harz eingebettete biologische Proben), Ionenmahlen oder fokussierte Ionenstrahlpräparation (z. B. Halbleiter-, poröse oder gemischte Härteproben, die nicht poliert werden können), mechanisches oder elektrochemisches Polieren (z. B. Metalllegierungen) oder Dünnschichtabscheidung (z. B. Atom...

Materialien

Name	Company	Catalog Number	Comments
Atomic force microscope	Bruker	Dimension Icon	Uses Nanoscope control software, including PeakForce Quantitative Nanomechanical Mapping (PF-QNM), FastForce Volume (FFV), and Point-and-Shoot Ramping experimental workspaces
AtomicJ	American Institute of Physics	https://doi.org/10.1063/1.4881683	Flexible, powerful, free open source Java-based force curve analysis software package. Supports numerous contact mechanic models, such as Hertz, Sneddon DMT, JKR, Maugis, and cone or pyramid (including blunt and truncated). Also includes a variety of initial contact point estimation methods to choose from. Supports batch processing of data and subsequent statistical analysis (e.g., averages, standard deviations, histograms, goodness of fit, etc.). Literature citation is: P. Hermanowicz, M. Sarna, K. Burda, and H. Gabry, “AtomicJ: An open source software for analysis of force curves” Rev. Sci. Instrum. 85: 063703 (2014), https://doi.org/10.1063/1.4881683
Buffer solution (PBS)	Fisher Chemical (NaCl), Sigma Aldrich (KCl), Fisher BioReagents (Na2HPO4 and KH2PO4)	S271 (>99% purity NaCl), P9541 (>99% purity KCl), BP332(>99% purity Na2HPO4), BP362 (>99% purity KH2PO4)	Phosphate buffered saline (PBS) was prepared in the laboratory as an aqueous solution consisting of 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.8 mM KH2PO4 dissolved in ultrapure water. Reagents were measured out using an analytical balance, and glassware was cleaned with soap and water followed by autoclaving immediately prior to use.
Chloroform
Diamond tip AFM probe	Bruker	PDNISP	Pre-mounted factory-calibrated cube corner diamond (E = 1140 GPa) tip AFM probe (nominal R = 40 nm) with a stainless steel cantilever (nominal k = 225 N/m, f0 = 50 kHz). Spring constant is measured at the factory (k = 256 N/m for the probe, Serial #13435414, used here) and calibration data (including AFM images of indents showing probe geometry) is provided with the probe.
Diamond ultramicrotome blade	Diatome	Ultra 35°	2.1 mm width. Also used a standard glass blade for intial rough cut of sample surface before transitioning to diamond blade for final surface preparation
Epoxy	Gorilla Glue	26853-31-6	Epoxy resin and hardner were mixed in a 1:1 ratio, a small drop was placed on a stainless steel sample puck (Ted Pella), and V1 grade muscovite mica (Ted Pella) was attached to create an atomically flat surface for preparation of phospholipid membranes.
Ethanol
LR white resin, medium grade (catalyzed)	Electron Microscopy Sciences	14381	500 mL bottle, Lot #150629
Mesenchymal stem cells (MSCs)	N/A	N/A	MSCs for nanomechanical studies were primary cells harvested from 8-10 week old male C57BL/6 mice as described in Goelzer, M. et al. "Lamin A/C Is Dispensable to Mechanical Repression of Adipogenesis" Int J Mol Sci 22: 6580 (2021) doi:10.3390/ijms22126580 and Peister, A. et al. "Adult stem cells from bone marrow (MSCs) isolated from different strains of inbred mice vary in surface epitopes, rates of proliferation, and differentiation potential" Blood 103: 1662-1668 (2004), doi:10.1182/blood-2003-09-3070.
Modulus standards	Bruker	PFQNM-SMPKIT-12M	Used HOPG (E = 18 GPa) and PS (E = 2.7 GPa). Also contains 2x PDMS (Tack 0, E = 2.5 MPa; Tack 4, E = 3.5 MPa), PS-LDPE (E = 2.0/0.2 GPa), fused silica (E = 72.9 GPa), sapphire (E - 345 GPa), and tip characterization (titanium roughness) sample. All samples come pre-mounted on a 12 mm diameter steel disc (sample puck).
Muscovite mica	Ted Pella	50-12	12 mm diameter, V1 grade muscovite mica
Nanscope Analysis	Bruker	Version 2.0	Free AFM image processing and analysis software package, but designed for, and proprietary/limited to Bruker AFMs; similar functionality is available from free, platform-independent AFM image processing and analysis software packages such as Gwyddion, WSxM, and others. Has built-in capabilities for force curve analysis, but AtomicJ is more flexible/full featured (e.g., more built-in contact mechanics models to choose from, statistical analysis of force curve fitting results, etc.) for force curve analysis and handles batch processing of force curves.
Phospholipids: POPC, Cholesterol (ovine)	Avanti Polar Lipids	POPC: CAS # 26853-31-6, Cholesterol: CAS # 57-88-5	POPC lipid dissolved in chloroform (25 mg/mL) was obtained from vendor and used without further purification. Cholesterol powder from the same vendor was dissolved in chloroform (20 mg/mL).
Probe holder (fluid, lipid bilayers)	Bruker	MTFML-V2	Specific to the particular AFM used; MTFML-V2 is a glass probe holder for scanning in fluid on a MultiMode AFM.
Probe holder (fluid, MSCs)	Bruker	FastScan Bio Z-scanner	Used with Dimension FastScan head (XY flexure scanners). Serial number MXYPOM5-1B154.
Probe holder (standard, ambient)	Bruker	DAFMCH	Specific to the particular AFM used; DAFMCH is the standard contact and tapping mode probe holder for the Dimension Icon AFM, suitable for nanoindentation (PF-QNM, FFV, and point-and-shoot ramping)
Sample Puck	Ted Pella	16218	Product number is for 15 mm diameter stainless steel sample puck. Also available in 6 mm, 10 mm, 12 mm, and 20 mm diameters at https://www.tedpella.com/AFM_html/AFM.aspx#anchor842459
Sapphire substrate	Bruker	PFQNM-SMPKIT-12M	Extremely hard surface (E = 345 GPa) for measuring deflection sensitivity of probes (want all of the deflection to come from the probe, not the substrate). Part of the PF-QNM/modulus standards kit.
Scanning electron microscope	Hitachi	S-3400N-II	Located at Boise State. Used to perform co-localized SEM/EDS on all samples except additively manufactured (AM) Ti-6Al-4V.
Silicon AFM probes (standard)	NuNano	Scout 350	Standard tapping mode silicon probe with reflective aluminum backside coating; k = 42 N/m (nominal), f0 = 350 kHz. Nominal R = 5 nm. Also available uncoated or with reflective gold backside coating. Probes with similar specifications are available from other manufacturers (e.g., Bruker TESPA-V2).
Silicon AFM probes (stiff)	Bruker	RTESPA-525, RTESPA-525-30	Rotated tip etched silicon probes with reflective aluminum backside coating; k = 200 N/m (nominal), f0 = 525 kHz. Nominal R = 8 nm for RTESPA-525, R = 30 nm for RTESPA-525-30. Spring constant of each RTESPA-525-30 is measured individually at the factory via laser Doppler vibrometry and supplied with the probe.
Silicon carbide grit paper (abrasive discs)	Allied	50-10005	120 grit
Silicon nitride AFM probes (soft, large radius hemispherical tip)	Bruker	MLCT-SPH-5UM, MLCT-SPH-5UM-DC	Also MLCT-SPH-1UM-DC. New product line of factory-calibrated (probe radius and spring constants of all cantilevers) large radius (R = 1 or 5 mm) hemispherical tip (at the end of a 23 mm long cylindrical shaft) probes. DC = drift compensation coating. 6 cantilevers/probe (A-F). Nominal spring constants: A, k = 0.07 N/m; B, k = 0.02 N/m; C, k = 0.01 N/m; D, k = 0.03 N/m; E, k = 0.1 N/m; F, k = 0.6 N/m.
Silicon nitride AFM probes (soft, medium sharp tip)	Bruker	DNP	4 cantilevers/probe (A-d). Nominal spring constants: A, k = 0.35 N/m; B, k = 0.12 N/m; C, k = 0.24 N/m; D, k = 0.06 N/m. Nominal radii of curvature, R = 10 nm.
Silicon nitride AFM probes (soft, sharp tip)	Bruker	ScanAsyst-Air	Nominal values: resonance frequency, f0 = 70 kHz; spring constant, k = 0.4 N/m; radius of curvature, R = 2 nm. Designed for force curve based AFM imaging.
Superglue	Henkel	Loctite 495	Cyanoacrylate based instant adhesive. Lots of roughly equivalent products are readily available.
Syringe pump	New Era Pump Systems	NE1000US	One channel syringe pump system with infusion and withdrawal capacity
Tip characterization standard	Bruker	PFQNM-SMPKIT-12M	Titanium (Ti) roughness standard. Part of the PF-QNM/modulus standards kit.
Ultrahigh purity nitrogen (UHP N2), 99.999%	Norco	SPG TUHPNI - T	T size compressed gas cylinder of ultrahigh purity (99.999%) nitrogen for drying samples
Ultramicrotome	Leica	EM UC6	Equipped with a glass blade (standard, for intial sample preparation) and a diamond blade (for final preparation)
Ultrapure water	Thermo Fisher	Barnstead Nanopure Model 7146	Model has been discontinued, but equivalent products are available. Produces ≥18.2 MΩ*cm ultrapure water with 1-5 ppb TOC (total organic content), per inline UV monitoring. Includes 0.2 µm particulate filter, ion exchange columns, and UV oxidation chamber.
Variable Speed Grinder	Buehler	EcoMet 3000	Used with silicon carbide grit papers during hand polishing.
Vibration isolation table (active)	Herzan	TS-140	Used with Bruker MultiMode AFM. Sits on a TMC 65-531 vibration isolation table. Bruker Dimension Icon AFM utilizes strictly passive vibration isolation (comes from manufacturer with custom acoustic hood, air table, and granite slab).
Vibration isolation table (passive)	TMC	65-531	35" x 30" vibration isolation table with optional air damping (disabled). Used with Bruker MultiMode AFM. Herzan TS-140 "Table Stable" active vibration control table is located on top.