Microscopia a forza atomica Nanoindentazione basata su sbalzo: misure di proprietà meccaniche su scala nanometrica in aria e fluido

Riepilogo

La quantificazione dell'area di contatto e della forza applicata dalla punta di una sonda a forza atomica (AFM) su una superficie del campione consente la determinazione delle proprietà meccaniche su scala nanometrica. Vengono discusse le migliori pratiche per implementare la nanoindentazione basata su sbalzo AFM in aria o fluido su campioni morbidi e duri per misurare il modulo elastico o altre proprietà nanomeccaniche.

Abstract

Un microscopio a forza atomica (AFM) misura fondamentalmente l'interazione tra la punta di una sonda AFM su scala nanometrica e la superficie del campione. Se la forza applicata dalla punta della sonda e la sua area di contatto con il campione possono essere quantificate, è possibile determinare le proprietà meccaniche su scala nanometrica (ad esempio, elastico o modulo di Young) della superficie da sondare. Qui viene fornita una procedura dettagliata per eseguire esperimenti quantitativi di nanoindentazione basati su cantilever AFM, con esempi rappresentativi di come la tecnica può essere applicata per determinare i moduli elastici di un'ampia varietà di tipi di campione, che vanno da kPa a GPa. Questi includono cellule staminali mesenchimali vive (MSC) e nuclei in tampone fisiologico, sezioni trasversali di pino loblolly disidratate incorporate in resina e scisti di Bakken di varia composizione.

Inoltre, la nanoindentazione basata su sbalzo AFM viene utilizzata per sondare la resistenza alla rottura (cioè la forza di rottura) dei doppi strati fosfolipidici. Importanti considerazioni pratiche come la scelta e lo sviluppo del metodo, la selezione e la calibrazione della sonda, l'identificazione della regione di interesse, l'eterogeneità del campione, le dimensioni e le proporzioni delle caratteristiche, l'usura della punta, la rugosità della superficie e l'analisi dei dati e le statistiche di misurazione sono discusse per aiutare la corretta implementazione della tecnica. Infine, viene dimostrata la co-localizzazione di mappe nanomeccaniche derivate da AFM con tecniche di microscopia elettronica che forniscono ulteriori informazioni sulla composizione elementare.

Introduzione

Comprendere le proprietà meccaniche dei materiali è uno dei compiti più fondamentali ed essenziali in ingegneria. Per l'analisi delle proprietà dei materiali sfusi, sono disponibili numerosi metodi per caratterizzare le proprietà meccaniche dei sistemi di materiali, tra cui prove di trazione¹, prove di compressione² e prove di flessione (flessione) a tre o quattro punti³. Mentre questi test su microscala possono fornire informazioni preziose sulle proprietà dei materiali sfusi, sono generalmente condotti fino al fallimento e sono quindi distruttivi. Inoltre, mancano della risoluzione spaziale necessaria per studiare accuratamente le proprietà su micro e nanoscala di molti sistemi di materiali che sono di interesse oggi, come film sottili, materiali biologici e nanocompositi. Per iniziare ad affrontare alcuni dei problemi con i test meccanici su larga scala, principalmente la loro natura distruttiva, i test di microdurezza sono stati adottati dalla mineralogia. La durezza è una misura della resistenza di un materiale alla deformazione plastica in condizioni specifiche. In generale, i test di microdurezza utilizzano una sonda rigida, solitamente realizzata in acciaio temprato o diamantato, per rientrare in un materiale. La profondità di indentazione e/o l'area risultanti possono quindi essere utilizzate per determinare la durezza. Sono stati sviluppati diversi metodi, tra cui Vickers⁴, Knoop⁵ e Brinell⁶ durezza; Ognuno fornisce una misura della durezza del materiale su microscala, ma in condizioni e definizioni diverse, e come tale produce solo dati che possono essere confrontati con test eseguiti nelle stesse condizioni.

La nanoindentazione strumentata è stata sviluppata per migliorare i valori relativi ottenuti tramite i vari metodi di test di microdurezza, migliorare la risoluzione spaziale possibile per l'analisi delle proprietà meccaniche e consentire l'analisi di film sottili. È importante sottolineare che, utilizzando il metodo sviluppato per la prima volta da Oliver e Pharr⁷, l'elastico o modulo di Young, E, di un materiale campione può essere determinato tramite nanoindentazione strumentata. Inoltre, utilizzando una sonda nanoindentatrice piramidale a tre lati Berkovich (la cui funzione di area ideale della punta corrisponde a quella della sonda piramidale a quattro lati Vickers)⁸, è possibile effettuare un confronto diretto tra le misurazioni della durezza su scala nanometrica e su microscala più tradizionali. Con la crescita della popolarità dell'AFM, anche la nanoindentazione basata su sbalzo AFM ha iniziato a ricevere attenzione, in particolare per misurare le proprietà meccaniche dei materiali più morbidi. Di conseguenza, come illustrato schematicamente nella Figura 1, le due tecniche più comunemente impiegate oggi per interrogare e quantificare le proprietà meccaniche su scala nanometrica sono la nanoindentazione strumentata (Figura 1A) e la nanoindentazione basata su sbalzo AFM (Figura 1B)⁹, l'ultima delle quali è il fulcro di questo lavoro.

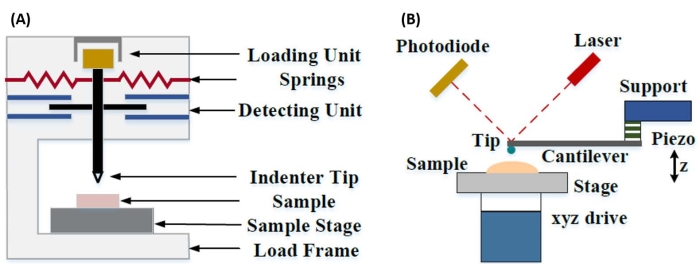
Figura 1: Confronto tra sistemi di nanoindentazione strumentati e basati su cantilever AFM. Diagrammi schematici che illustrano i sistemi tipici per condurre (A) nanoindentazione strumentata e (B) nanoindentazione a sbalzo AFM. Questa cifra è stata modificata da Qian et ^al.51. Abbreviazione: AFM = microscopia a forza atomica. Fare clic qui per visualizzare una versione ingrandita di questa figura.

Sia la nanoindentazione strumentata che quella basata su sbalzo AFM impiegano una sonda rigida per deformare una superficie campione di interesse e monitorare la forza risultante e lo spostamento in funzione del tempo. Tipicamente, il carico desiderato (cioè forza) o il profilo di spostamento (Z-piezo) viene specificato dall'utente tramite l'interfaccia software e controllato direttamente dallo strumento, mentre viene misurato l'altro parametro. La proprietà meccanica più spesso ottenuta da esperimenti di nanoindentazione è il modulo elastico (E), noto anche come modulo di Young, che ha unità di pressione. Il modulo elastico di un materiale è una proprietà fondamentale relativa alla rigidezza del legame ed è definito come il rapporto tra la tensione di trazione o compressione (σ, la forza applicata per unità di area) e la deformazione assiale (ε, la deformazione proporzionale lungo l'asse di indentazione) durante la deformazione elastica (cioè reversibile o temporanea) prima dell'inizio della deformazione plastica (equazione 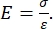[1]):

(1)

Va notato che, poiché molti materiali (soprattutto i tessuti biologici) sono in realtà viscoelastici, in realtà il modulo (dinamico o complesso) è costituito sia da componenti elastiche (stoccaggio, in fase) che viscose (perdita, fuori fase). In pratica, ciò che viene misurato in un esperimento di nanoindentazione è il modulo ridotto, E *, che è correlato al vero modulo campione di interesse, E, come mostrato nell'equazione 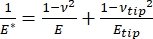(2):

(2)

Dove punta E e punta ν sono rispettivamente il modulo elastico e il rapporto di Poisson della punta del nanopenetratore, e ν è il rapporto di Poisson stimato del campione. Il rapporto di Poisson è il rapporto negativo tra la deformazione trasversale e quella assiale, e quindi indica il grado di allungamento trasversale di un campione dopo essere sottoposto a deformazione assiale (ad esempio, durante il carico di nanoindentazione), come mostrato nell'equazione 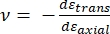(3):

(3)

La conversione dal modulo ridotto a quello effettivo è necessaria perché a) parte della deformazione assiale impartita dalla punta del penetratore può essere convertita in deformazione trasversale (cioè, il campione può deformarsi per espansione o contrazione perpendicolare alla direzione di carico), e b) la punta del penetratore non è infinitamente dura, e quindi l'atto di indentare il campione provoca una certa (piccola) quantità di deformazione della punta. Si noti che nel caso in cui la punta E >> E (cioè la _punta del penetratore è molto più dura del campione, il che è spesso vero quando si utilizza una sonda diamantata), la relazione tra il modulo del campione ridotto e quello effettivo si semplifica notevolmente in E ≈ E*(1 - v²). Mentre la nanoindentazione strumentata è superiore in termini di accurata caratterizzazione della forza e gamma dinamica, la nanoindentazione basata su sbalzo AFM è più veloce, fornisce ordini di grandezza maggiore forza e sensibilità allo spostamento, consente immagini a risoluzione più elevata e una migliore localizzazione dell'indentazione e può simultaneamente sondare proprietà magnetiche ed elettriche su scala nanometrica⁹. In particolare, la nanoindentazione basata su sbalzo AFM è superiore per la quantificazione delle proprietà meccaniche su scala nanometrica di materiali morbidi (ad esempio, polimeri, gel, doppi strati lipidici e cellule o altri materiali biologici), film estremamente sottili (sub-μm) (dove gli effetti del substrato possono entrare in gioco a seconda della profondità di indentazione)^10,11 e materiali bidimensionali sospesi (2D)^12,13,14 come il grafene ^15,16, mica 17, nitruro di boro esagonale (h-BN)¹⁸ o dichalcogenuri dei metalli di transizione (TMDC; ad esempio, MoS₂)¹⁹. Ciò è dovuto alla sua squisita sensibilità alla forza (sub-nN) e allo spostamento (sub-nm), che è importante per determinare con precisione il punto di contatto iniziale e rimanere all'interno della regione di deformazione elastica.

Nella nanoindentazione a sbalzo AFM, lo spostamento di una sonda AFM verso la superficie del campione viene azionato da un elemento piezoelettrico calibrato (Figura 1B), con il cantilever flessibile che alla fine si piega a causa della forza resistiva sperimentata al contatto con la superficie del campione. Questa flessione o deflessione del cantilever viene tipicamente monitorata riflettendo un laser sul retro del cantilever e in un fotorivelatore (rilevatore sensibile alla posizione [PSD]). Insieme alla conoscenza della rigidità a sbalzo (in nN/nm) e della sensibilità alla deflessione (in nm/V), è possibile convertire questa deflessione a sbalzo misurata (in V) nella forza (in nN) applicata al campione. Dopo il contatto, la differenza tra il movimento Z-piezo e la deflessione a sbalzo produce la profondità di indentazione del campione. In combinazione con la conoscenza della funzione dell'area della punta, ciò consente di calcolare l'area di contatto punta-campione. La pendenza delle porzioni di contatto delle curve forza-distanza o forza-spostamento (F-D) risultanti può quindi essere adattata utilizzando un modello di meccanica di contatto appropriato (vedere la sezione Analisi dei dati della discussione) per determinare le proprietà nanomeccaniche del campione. Mentre la nanoindentazione basata su sbalzo AFM possiede alcuni vantaggi distinti rispetto alla nanoindentazione strumentata come descritto sopra, presenta anche diverse sfide pratiche di implementazione, come la calibrazione, l'usura della punta e l'analisi dei dati, che saranno discusse qui. Un altro potenziale svantaggio della nanoindentazione basata su AFM a sbalzo è l'ipotesi di elasticità lineare, poiché il raggio di contatto e le profondità di indentazione devono essere molto più piccoli del raggio del penetratore, che può essere difficile da ottenere quando si lavora con sonde AFM su scala nanometrica e / o campioni che mostrano rugosità superficiale significativa.

Tradizionalmente, la nanoindentazione è stata limitata a singole posizioni o piccoli esperimenti di indentazione della griglia, in cui viene selezionata una posizione desiderata (ad esempio, la regione di interesse [ROI]) e viene eseguito un singolo rientro controllato, più rientri in una singola posizione separati da un certo tempo di attesa e / o una griglia grossolana di rientri vengono eseguiti a una frequenza dell'ordine di Hz. Tuttavia, i recenti progressi nell'AFM consentono l'acquisizione simultanea di proprietà meccaniche e topografia attraverso l'utilizzo di modalità di imaging basate su curve di forza ad alta velocità (indicate da vari nomi commerciali a seconda del produttore del sistema), in cui le curve di forza sono condotte a una velocità di kHz sotto controllo del carico, con la massima forza del campione di punta utilizzata come setpoint di imaging. Sono stati inoltre sviluppati metodi point-and-shoot, che consentono l'acquisizione di un'immagine topografica AFM seguita da una successiva nanoindentazione selettiva nei punti di interesse all'interno dell'immagine, offrendo un controllo spaziale su scala nanometrica sulla posizione della nanoindentazione. Sebbene non sia l'obiettivo principale di questo lavoro, esempi specifici di applicazione selezionati sia di imaging basato sulla curva di forza che di nanoindentazione basata su cantilever point-and-shoot sono presentati nei risultati rappresentativi e possono essere utilizzati in combinazione con il protocollo descritto di seguito, se disponibile sulla particolare piattaforma AFM utilizzata. In particolare, questo lavoro delinea un protocollo generalizzato per l'implementazione pratica della nanoindentazione a sbalzo AFM su qualsiasi sistema AFM capace e fornisce quattro esempi di casi d'uso (due in aria, due in fluido) della tecnica, inclusi risultati rappresentativi e una discussione approfondita delle sfumature, delle sfide e delle considerazioni importanti per impiegare con successo la tecnica.

Protocollo

NOTA: A causa dell'ampia varietà di AFM disponibili in commercio e della diversità dei tipi di campioni e delle applicazioni esistenti per la nanoindentazione basata su cantilever, il protocollo che segue è intenzionalmente progettato per essere di natura relativamente generale, concentrandosi sui passaggi condivisi necessari per tutti gli esperimenti di nanoindentazione basati su cantilever, indipendentemente dallo strumento o dal produttore. Per questo motivo, gli autori presumono che il lettore possieda almeno una familiarità di base con il funzionamento dello strumento specifico scelto per eseguire la nanoindentazione basata su cantilever. Tuttavia, oltre al protocollo generale descritto di seguito, una dettagliata procedura operativa standard passo-passo (SOP) specifica per l'AFM e il software utilizzato qui (vedi Tabella dei materiali), incentrata sulla nanoindentazione a sbalzo dei campioni nel fluido, è inclusa come materiale supplementare.

1. Preparazione del campione e configurazione dello strumento

1. Preparare il campione in modo da ridurre al minimo sia la rugosità superficiale (idealmente su scala nanometrica, ~ 10 volte inferiore alla profondità di indentazione prevista) sia la contaminazione senza alterare le proprietà meccaniche dell'area o delle aree di interesse.
2. Selezionare una sonda AFM appropriata per la nanoindentazione del campione previsto in base al mezzo (cioè aria o fluido), al modulo previsto, alla topografia del campione e alle dimensioni delle caratteristiche rilevanti (vedere le considerazioni sulla selezione della sonda nella discussione). Caricare la sonda sul supporto della sonda (vedere la tabella dei materiali) e collegare il supporto della sonda alla testa di scansione AFM.
3. Selezionare una modalità di nanoindentazione appropriata nel software AFM che offra all'utente il controllo delle singole rampe (ad esempio, curve di forza-spostamento).
   NOTA: La modalità specifica differirà tra i diversi produttori di AFM e i singoli strumenti (vedere SOP fornita nel materiale supplementare per maggiori dettagli e un esempio specifico).
4. Allineare il laser sul retro del cantilever della sonda, di fronte alla posizione della punta della sonda e nel PSD.
   NOTA: Vedere l'esempio di applicazione delle cellule staminali mesenchimali per maggiori dettagli su considerazioni importanti quando si allinea il laser e si conduce la nanoindentazione nel fluido, in particolare, evitando detriti galleggianti e / o bolle d'aria, che possono disperdere o rifrangere il raggio. Potrebbe anche essere necessario regolare l'ottica AFM per compensare l'indice di rifrazione del fluido ed evitare di schiantare la sonda quando si innesta la superficie.
   1. Centrare lo spot del raggio laser sul retro del cantilever massimizzando la tensione di somma (Figura 2A).
   2. Centrare lo spot del raggio laser riflesso sul PSD regolando i segnali di deflessione X e Y (cioè orizzontale e verticale) in modo che siano il più vicino possibile allo zero (Figura 2A), fornendo così il massimo intervallo di deflessione rilevabile per produrre una tensione di uscita proporzionale alla deflessione a sbalzo.
5. Se non si è sicuri della topografia del campione, della rugosità superficiale e/o della densità superficiale (nel caso di scaglie o particelle), eseguire una scansione topografica AFM prima di qualsiasi esperimento di nanoindentazione per confermare l'idoneità del campione, come descritto nella fase 1.1 e nella parte di preparazione del campione della discussione.

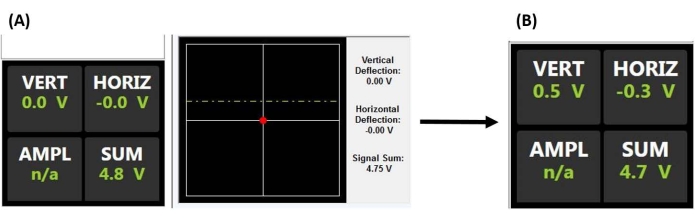
Figura 2: Monitor del rilevatore sensibile alla posizione. (A) Display PSD che indica un laser correttamente allineato che si riflette sul retro della sonda a sbalzo e sul centro del PSD (come evidenziato dalla grande tensione di somma e dalla mancanza di deflessione verticale o orizzontale) prima di innestarsi sulla superficie del campione (cioè sonda fuori contatto con il campione). (B) La tensione di deflessione verticale aumenta quando il cantilever viene deviato (ad esempio, quando la sonda entra in contatto con il campione). Abbreviazioni: PSD = rilevatore sensibile alla posizione; VERT = verticale; HORIZ = orizzontale; AMPL = ampiezza; n/d = non applicabile. Fare clic qui per visualizzare una versione ingrandita di questa figura.

2. Calibrazione della sonda

NOTA: Sono necessari tre valori per quantificare le proprietà meccaniche di un campione utilizzando i dati della curva F-D raccolti durante la nanoindentazione a sbalzo: la sensibilità di deflessione (DS) del sistema a sbalzo/PSD (NM/V o V/nm), la costante della molla a sbalzo (nN/nm) e l'area di contatto della sonda, spesso espressa in termini di raggio effettivo della punta della sonda (nm) ad una data profondità di indentazione inferiore al raggio della sonda nel caso di una sonda sferica mancia.

1. Calibrare il DS del sistema sonda/AFM facendo ramping su un materiale estremamente duro (ad esempio, zaffiro, E = 345 GPa) in modo che la deformazione del campione sia ridotta al minimo e quindi il movimento Z misurato del piezo dopo l'inizio del contatto punta-campione venga convertito esclusivamente in deflessione a sbalzo.
   NOTA: La calibrazione DS deve essere eseguita nelle stesse condizioni degli esperimenti di nanoindentazione pianificati (cioè temperatura, mezzo, ecc.) per riflettere accuratamente il DS del sistema durante gli esperimenti. Un lungo periodo di riscaldamento laser (30 minuti) può essere necessario per la massima precisione per consentire il raggiungimento dell'equilibrio termico e la stabilità della potenza di uscita del laser stabile e della stabilità di puntamento. Il DS deve essere rimisurato ogni volta che il laser viene riallineato, anche se viene utilizzata la stessa sonda, poiché il DS dipende dall'intensità e dalla posizione del laser sul cantilever, nonché dalla qualità della riflessione della sonda (ad esempio, la degradazione del rivestimento posteriore della sonda influenzerà il DS) e dalla sensibilità della PSD²⁰.
   1. Impostare ed eseguire le impronte di calibrazione DS sullo zaffiro per ottenere approssimativamente la stessa deflessione della sonda (in V o nm) dei rientri del campione pianificati, poiché lo spostamento misurato è una funzione dell'angolo di deflessione della punta e diventa non lineare per grandi deflessioni.
   2. Determinare il DS (in nm/V) o, in alternativa, la sensibilità della leva ottica inversa (in V/nm), dalla pendenza della porzione lineare del regime di contatto dopo il punto di contatto iniziale nella curva F-D risultante, come mostrato nella Figura 3A.
   3. Ripetere la rampa almeno 5x, registrando ogni valore DS. Utilizzare la media dei valori per la massima precisione. Se la deviazione standard relativa (RSD) delle misurazioni supera ~ 1%, rimisurare il DS, poiché a volte le prime curve F-D non sono ideali a causa dell'introduzione iniziale di forze di attrazione.
   4. Se la costante della molla del cantilever, k, non è calibrata in fabbrica (ad esempio, tramite vibrometria laser Doppler [LDV]), calibrare la costante della molla.
      NOTA: Il metodo di regolazione termica è ottimale per cantilever relativamente morbidi con k < 10 N/m (vedere la sezione costante di molla della discussione per un elenco e una descrizione dei metodi alternativi, in particolare per i cantilever rigidi con k > 10 N/m). Come mostrato nella Figura 3B, C, la regolazione termica è tipicamente integrata nel software di controllo AFM.
2. Se la sonda non viene fornita con una misurazione del raggio di punta calibrata in fabbrica (ad esempio, tramite imaging al microscopio elettronico a scansione [SEM]), misurare il raggio di punta effettivo, R.
   NOTA: Esistono due metodi comuni per misurare il raggio della punta (vedere la sezione di discussione corrispondente), ma il più comune per le punte della sonda su scala nanometrica è il metodo della ricostruzione della punta cieca (BTR), che utilizza uno standard di rugosità (vedi Tabella dei materiali) contenente numerose caratteristiche estremamente nitide (sub-nm) che servono a visualizzare efficacemente la punta, piuttosto che l'immagine della punta del campione.
   1. Se si utilizza il metodo BTR, visualizzare il campione di rugosità (caratterizzazione della punta) utilizzando una frequenza di scansione lenta (<0,5 Hz) e guadagni di feedback elevati per ottimizzare il tracciamento delle caratteristiche molto nitide. Scegli una dimensione dell'immagine e una densità di pixel (risoluzione) in base al raggio di punta previsto (ad esempio, un'immagine di 1024 x 1024 pixel di un'area di 3 μm x 3 μm avrà una risoluzione laterale di ~ 3 nm).
   2. Utilizzare il software di analisi delle immagini AFM (vedere la tabella dei materiali) per modellare la punta della sonda e stimarne il raggio finale e il diametro effettivo della punta alla profondità di rientranza del campione prevista, come mostrato nella Figura 3D-F.
3. Dopo aver completato la calibrazione della sonda, immettere i valori DS, k e R nel software dello strumento, come mostrato nella Figura 4A.
   1. Immettere una stima del rapporto di Poisson del campione, ν, per consentire la conversione del modulo ridotto misurato nel^{modulo 9 effettivo} del campione. Se si utilizza un modello di meccanica di contatto conico o conisferico basato sulla forma della punta e sulla profondità di indentazione, è necessario inserire anche il semiangolo della punta (Figura 4C).
      NOTA: Il modulo è relativamente insensibile a piccoli errori o incertezze nel rapporto di Poisson stimato. Una stima di ν = 0,2-0,3 è un buon punto di partenza per molti materiali²¹.

Figura 3: Taratura della sonda. (A) Determinazione della sensibilità alla deflessione. Risultato di una misura rappresentativa della sensibilità alla deflessione effettuata su un substrato di zaffiro (E = 345 GPa) per una sonda standard della modalità maschiatura (k nominale = 42 N/m; vedi Tabella dei materiali) con un rivestimento in alluminio riflettente. Vengono mostrati l'approccio misurato (traccia blu) e le curve di retrazione o ritiro (traccia rossa). La sensibilità di deflessione misurata di 59,16 nm/V è stata determinata adattando la curva di attacco tra i punti di contatto a scatto e di turn-around, come indicato dalla regione tra le linee rosse tratteggiate verticali. La regione di deflessione negativa evidente nella curva di ritrazione/prelievo prima di staccare la superficie è indicativa dell'adesione punta-campione. (B,C) Sintonizzazione termica. Spettri di rumore termico a sbalzo rappresentativi (tracce blu) con corrispondenti adattamenti (tracce rosse) per due diverse sonde. (B) Impostazione della regolazione termica e parametri di adattamento per una sonda di imaging AFM basata sulla curva di forza standard (vedi Tabella dei materiali) con la sua costante nominale della molla k = 0,4 N/m utilizzata come ipotesi iniziale. L'adattamento dello spettro di rumore termico a sbalzo produce una frequenza di risonanza fondamentale di f 0 = 79,8 kHz, che è ragionevolmente in accordo con il valore nominale di f₀ = 70 kHz. Il fattore Q misurato è 58,1. La bontà di adattamento (R² = 0,99) si basa sull'accordo dell'adattamento con i dati tra le due linee rosse tratteggiate verticali. Si noti che è importante conoscere e inserire sia la temperatura ambiente che la sensibilità alla deflessione per risultati accurati. (C) Spettro di rumore termico a sbalzo e adattamento corrispondente (cioè sintonizzazione termica) con costante di molla calcolata risultante k = 0,105 N/m per un cantilever estremamente morbido utilizzato per eseguire misure nanomeccaniche su cellule vive e nuclei isolati. Si noti la frequenza di risonanza naturale significativamente più bassa di ~ 2-3 kHz. (D-F) Ricostruzione della punta cieca. Flusso di lavoro rappresentativo di ricostruzione della punta cieca per una sonda a punta diamantata (nominale R = 40 nm; vedi tabella dei materiali). (D) Un'immagine di 5 μm x 5 μm di un campione di caratterizzazione della punta costituito da una serie di punte di titanio estremamente nitide (sub-nm) che servono a fotografare la punta della sonda AFM. (E) Modello ricostruito risultante (immagine in altezza invertita) della punta della sonda. (F) Risultati del raccordo di ricostruzione della punta cieca, compreso un raggio finale stimato di R = 29 nm e un diametro effettivo della punta di 40 nm ad un'altezza selezionata dall'utente di 8 nm (cioè profondità di rientro << R) dall'apice della punta, calcolati convertendo l'area di contatto punta-campione a tale altezza in un diametro effettivo assumendo un profilo circolare (cioè A = πr 2 = π(d/2)²) per l'uso con modelli di meccanica a contatto sferico. Abbreviazioni: AFM = microscopia a forza atomica; ETD = diametro effettivo della punta. Fare clic qui per visualizzare una versione ingrandita di questa figura.

Figura 4: Input dell'interfaccia software. (A) Costanti di taratura della sonda. Interfaccia utente del software (vedere Tabella dei materiali) per inserire la sensibilità di deflessione misurata, la costante della molla e il raggio della punta per consentire misurazioni nanomeccaniche quantitative. Il rapporto di Poisson sia della sonda che del campione è necessario per calcolare l'elastico o il modulo di Young del campione dalle curve di forza di nanoindentazione basate su cantilever. (B) Finestra di controllo della rampa. Interfaccia utente software (vedi Tabella dei materiali) per l'impostazione di esperimenti di nanoindentazione basati su cantilever, organizzati nei parametri che descrivono la rampa stessa (cioè il profilo di indentazione), l'innesco dello strumento (ad esempio, il controllo della forza rispetto allo spostamento), la successiva analisi della forza e i limiti di movimento (per migliorare la sensibilità di misura restringendo l'intervallo su cui il convertitore A / D deve operare nel controllo del piezo Z e nella lettura della deflessione PSD). (C) Il semiangolo della punta (basato sulla geometria della sonda o sulla misura diretta) è importante se viene impiegato un modello di meccanica di contatto conica, piramidale o conisferica (ad esempio, Sneddon). Fare clic qui per visualizzare una versione ingrandita di questa figura.

3. Raccogliere dati di spostamento della forza (F-D)

NOTA: i valori dei parametri qui presentati (vedere la Figura 4B) possono variare a seconda della forza e dell'intervallo di rientro per un determinato campione.

1. Naviga il campione sotto la testa AFM e interagisci sulla regione di interesse desiderata.
   1. Monitorare il segnale di deflessione verticale (Figura 2B) o eseguire una piccola rampa iniziale (~50-200 nm) (Figura 4B) per verificare che la punta e il campione siano in contatto (vedere Figura 5A).
   2. Regolare leggermente la posizione della testa AFM verso l'alto (in passi corrispondenti a ~ 50% della dimensione della rampa completa) e rampare di nuovo. Ripetere l'operazione fino a quando la punta e il campione non sono appena fuori contatto, come evidenziato da una rampa quasi piatta (Figura 5B) e da una minima deflessione verticale del cantilever (Figura 2A).
   3. Una volta che non è presente alcuna interazione evidente punta-campione (confrontare la Figura 2A e la Figura 2B ), abbassare la testa AFM di una quantità corrispondente a ~50%-100% della dimensione della rampa per garantire che la punta della sonda non si schianti contro il campione mentre si sposta manualmente la testa AFM. Rampa di nuovo, ripetendo fino a quando non si osserva una curva buona (Figura 5D) o una curva simile alla Figura 5C. In quest'ultimo caso, eseguire un'ulteriore piccola regolazione AFM di abbassamento della testa pari a ~ 20% -50% della dimensione della rampa per ottenere un buon contatto e una curva di forza simile a quella mostrata nella Figura 5D.
2. Regolare i parametri della rampa (come descritto di seguito e mostrato in Figura 4B) per ottimizzare lo strumento, la sonda e il campione, e ottenere rampe simili a quelle mostrate nella Figura 5D.
   1. Selezionare una dimensione di rampa appropriata (ad esempio, movimento totale Z-piezo attraverso un ciclo di rampa) a seconda del campione (ad esempio, spessore, modulo previsto, rugosità superficiale) e profondità di rientro desiderata.
      NOTA: Per i campioni più rigidi, è probabile che si verifichi una minore deformazione del campione (e quindi una maggiore deflessione della sonda per un dato movimento Z-piezoelettrico), quindi la dimensione della rampa può generalmente essere inferiore rispetto ai campioni più morbidi. Le dimensioni tipiche delle rampe per campioni rigidi e cantilever possono essere di decine di nm, mentre per campioni morbidi e rampe a sbalzo possono avere dimensioni comprese tra centinaia di nm e pochi μm; Esempi specifici di candidature selezionate sono presentati nella sezione Risultati rappresentativi. Si noti che le dimensioni minime e massime possibili delle rampe dipendono dallo strumento.
   2. Selezionare una frequenza di rampa appropriata (1 Hz è un buon punto di partenza per la maggior parte dei campioni).
      NOTA: La velocità di rampa può essere limitata da velocità/larghezze di banda elettroniche di controllo e/o rilevamento. In combinazione con la dimensione della rampa, la velocità della rampa determina la velocità della punta. La velocità della punta è particolarmente importante da considerare quando si indentano materiali morbidi in cui gli effetti viscoelastici possono causare artefatti di isteresi ^9,22.
   3. Scegli se utilizzare una rampa attivata (con controllo del carico) o non attivata (a spostamento controllato).
      NOTA: in una rampa attivata, il sistema si avvicina al campione in fasi definite dall'utente (in base alle dimensioni della rampa e alla risoluzione o al numero di punti dati) fino a quando non viene rilevata la soglia di attivazione desiderata (ad esempio, forza di setpoint o deflessione a sbalzo), a quel punto il sistema si ritrarrà nella sua posizione originale e visualizzerà la curva F-D. In una rampa non attivata, il sistema estende semplicemente il piezo Z alla distanza specificata dalla dimensione della rampa definita dall'utente e visualizza la curva F-D misurata. Le rampe attivate sono preferite per la maggior parte dei casi d'uso, ma le rampe non attivate possono essere utili quando si studiano materiali morbidi che non presentano un punto di contatto nitido e facilmente identificabile.
      1. Se si sceglie una rampa attivata, impostare la soglia di attivazione (forza massima consentita definita dall'utente o deflessione della rampa) per ottenere il rientro desiderato nel campione.
         NOTA: l'uso di una soglia di trigger significa che una rampa può terminare (cioè, la sonda può iniziare a ritrarsi) prima di raggiungere la dimensione completa della rampa (estensione Z-piezoelettrica) specificata. I valori possono variare da pochi nN a pochi μN, a seconda del sistema di campionamento della punta.
      2. Impostare la posizione della rampa per determinare la porzione della portata massima del piezo Z che verrà utilizzata per eseguire la rampa . Assicurarsi che l'intervallo totale della dimensione della rampa non inizi o finisca al di fuori dell'intervallo massimo Z-piezo (vedere esempi rappresentativi nella Figura 6), altrimenti una porzione della curva F-D non rappresenterà alcuna misura fisica (cioè, il piezo Z sarà completamente esteso o retratto, non in movimento).
   4. Impostare il numero di campioni/rampa (ad esempio, 512 campioni/rampa ) per ottenere la risoluzione desiderata della misura (cioè la densità puntiforme della curva F-D).
      NOTA: i campioni/rampe massimi possono essere limitati da vincoli software (dimensioni del file) o hardware (ad esempio, velocità di conversione da analogico a digitale [A/D], a seconda della velocità di rampa). È anche possibile limitare l'intervallo Z-piezoelettrico o di deflessione consentito (vedere i parametri limite nella Figura 4B) per aumentare la risoluzione effettiva del convertitore A/D del sistema.
   5. Impostare la rotazione a X per ridurre le forze di taglio sul campione e sulla punta spostando simultaneamente leggermente la sonda nella direzione X (parallela al cantilever) mentre si rientrava nella direzione Z (perpendicolare al cantilever). Utilizzare un valore per la rotazione a X uguale all'angolo di offset del supporto della sonda rispetto alla normale alla superficie (12° è tipico).
      NOTA: La rotazione a X è necessaria perché il cantilever è montato nel supporto della sonda con una piccola angolazione rispetto alla superficie per consentire al raggio laser incidente di riflettersi nella PSD. Inoltre, gli angoli anteriore e posteriore della punta della sonda possono differire l'uno dall'altro (cioè, la punta della sonda può essere asimmetrica). Informazioni più specifiche possono essere ottenute dai singoli produttori di sonde e AFM.

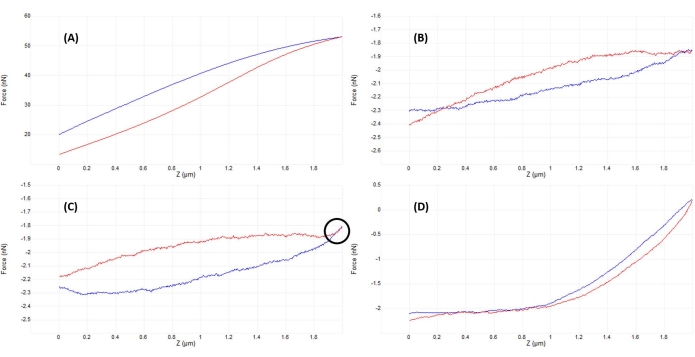
Figura 5: Ottimizzazione della separazione punta-campione dopo l'innesto per ottenere buone curve di forza. Esempi sequenziali di curve rappresentative forza-spostamento ottenute durante l'indentazione in fluido (soluzione salina tamponata con fosfato) su un nucleo di cellule staminali mesenchimali vive con un cantilever calibrato di nitruro di silicio morbido (k nominale = 0,04 N/m) terminante in una punta emisferica di raggio di 5 μm (vedi Tabella dei materiali). Le curve sono state ottenute nel processo di coinvolgimento della superficie cellulare e ottimizzazione dei parametri di indentazione, con l'approccio della sonda mostrato in blu e la ritrazione / ritiro in rosso. (A) La punta è già impegnata e a contatto con il campione prima di iniziare la rampa, con conseguente grande deflessione a sbalzo e forze, senza una linea di base piatta di precontatto. (B) Dopo aver spostato manualmente la punta sufficientemente lontano dal campione, una rampa di 2 μm non attivata produce una curva F-D quasi piatta (cioè praticamente nessuna variazione di forza). In condizioni ambientali, la curva sarebbe più piatta, ma in fluido, la viscosità del fluido può causare lievi deflessioni del cantilever della sonda durante una rampa come si vede qui, anche senza contatto superficiale. (C) Dopo essersi avvicinati leggermente alla superficie prima di iniziare la rampa, le curve di avvicinamento e di ritrazione mostrano un leggero aumento della forza (maggiore pendenza) vicino al punto di inversione della rampa (cioè transizione dall'avvicinamento al ritiro). Il segno rivelatore da cercare è che le curve di avvicinamento (blu) e ritiro (rosso) iniziano a sovrapporsi (regione indicata dal cerchio nero), il che è indicativo di un'interazione fisica con la superficie. (D) Una curva F-D ideale acquisita dopo l'ottimizzazione dei parametri di rampa e avvicinandosi leggermente (~1 μm) più vicina alla superficie della cella rispetto a C in modo che la sonda trascorra circa metà della rampa a contatto con la cella, consentendo una deformazione sufficiente per adattarsi alla porzione di contatto della curva di avvicinamento e determinare il modulo elastico. La linea di base relativamente lunga, piatta e a bassa rumorosità rende più facile per l'algoritmo di raccordo determinare il punto di contatto. Abbreviazione: F-D = forza-spostamento. Fare clic qui per visualizzare una versione ingrandita di questa figura.

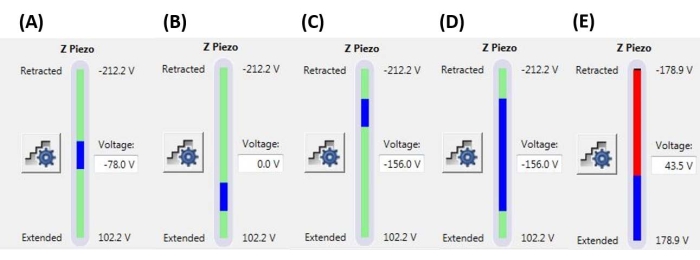
Figura 6: Dimensioni e posizione della rampa. Monitor Z-piezo che mostra l'estensione della rampa (barra blu) rispetto all'intervallo di movimento Z-piezoelettrico totale disponibile (barra verde). (A) La posizione Z-piezoelettrica è vicina alla metà del suo raggio di movimento, come indicato sia dalla barra blu che si trova approssimativamente al centro della barra verde sia dall'attuale tensione Z-piezoelettrica (-78,0 V) approssimativamente compresa tra i suoi valori completamente retratti (-212,2 V) ed estesi (+102,2 V). (B) Z-piezo è esteso rispetto ad A, senza tensione di polarizzazione applicata. (C) Z-piezo è retratto rispetto ad A e B. (D) La posizione Z-piezoelettrica è la stessa di C a -156,0 V, ma la dimensione della rampa è stata aumentata rispetto ad A-C per sfruttare maggiormente l'intera gamma di movimento del piezo Z. € La dimensione della rampa è troppo grande per la posizione attuale della rampa, con conseguente estensione del piezo Z fino alla fine del suo intervallo. Ciò causerà la linea piatta della curva F-D poiché il sistema non può estendere ulteriormente il piezo Z. Abbreviazione: F-D = forza-spostamento. Fare clic qui per visualizzare una versione ingrandita di questa figura.

4. Analisi della curva F-D

1. Scegliere un pacchetto software di analisi dei dati appropriato. Selezionare e caricare i dati da analizzare.
   NOTA: molti produttori AFM e programmi software di elaborazione delle immagini AFM dispongono di supporto integrato per l'analisi della curva F-D. In alternativa, la maggiore flessibilità e le caratteristiche di un pacchetto dedicato di analisi della curva F-D, come il pacchetto software open source AtomicJ, possono essere utili²³, in particolare per l'elaborazione in batch e l'analisi statistica di grandi set di dati o l'implementazione di complessi modelli di meccanica dei contatti.
2. Valori calibrati di input per la costante della molla, DS e raggio della punta della sonda, insieme alle stime del modulo di Young e del rapporto di Poisson per la punta della sonda (in base alla sua composizione materiale) e al rapporto di Poisson del campione.
   NOTA: se si utilizza un penetratore a punta diamantata, i valori E punta = 1140 GPa e _punta ν₌ 0,07 possono essere utilizzati^21,24,25,26. Per una sonda al silicio standard, E punta = 170 GPa e _punta ν₌ 0,27 possono tipicamente essere usati, anche se il modulo di Young del silicio varia a seconda dell'orientamento cristallografico²⁷.
3. Scegli un modello di meccanica a contatto di nanoindentazione appropriato per la punta e il campione.
   NOTA: Per i molti modelli di punta sferica comuni (ad esempio, Hertz, Maugis, DMT, JKR), è imperativo che la profondità di indentazione nel campione sia inferiore al raggio della punta; altrimenti la geometria sferica della punta della sonda lascia il posto a una forma conica o piramidale (Figura 4C). Per i modelli conici (ad esempio, Sneddon²⁸) e piramidali, il semiangolo della punta (cioè l'angolo tra la parete laterale della punta e una linea bisecante perpendicolare all'estremità della punta; Figura 4C) deve essere noto e di solito è disponibile presso il produttore della sonda. Per ulteriori informazioni sui modelli di meccanica dei contatti, consultare la sezione Analisi dei dati di thedDiscussion.
4. Eseguire l'algoritmo di raccordo. Verificare il corretto adattamento delle curve F-D; un basso errore residuo corrispondente a una media R 2 vicino all'unità (ad esempio, R² > 0,9) è tipicamente indicativo di una buona aderenza al modello scelto^29,30. Controllare a campione le singole curve per ispezionare visivamente la curva, l'adattamento del modello e i punti di contatto calcolati, se lo si desidera (ad esempio, vedere la Figura 7 e la sezione Analisi dei dati della discussione).

Risultati

Curve forza-spostamento
La Figura 7 mostra curve F-D rappresentative e quasi ideali ottenute da esperimenti di nanoindentazione eseguiti in aria su campioni di pino loblolly incorporati in resina (Figura 7A) e in fluido (soluzione salina tamponata con fosfato [PBS]) su nuclei di cellule staminali mesenchimali (MSC) (Figura 7B). L'uso di qualsiasi modello di meccanica di contatto si basa sulla determinazione accur...

Discussione

Preparazione del campione
Per la nanoindentazione in aria, i metodi di preparazione comuni includono la criosezione (ad esempio, campioni di tessuto), la macinazione e / o la lucidatura seguita da ultramicrotoming (ad esempio, campioni biologici incorporati in resina), la fresatura ionica o la preparazione di fasci ionici focalizzati (ad esempio, campioni di durezza semiconduttori, porosi o misti non suscettibili di lucidatura), lucidatura meccanica o elettrochimica (ad esempio, leghe metalliche) o de...

Materiali

Name	Company	Catalog Number	Comments
Atomic force microscope	Bruker	Dimension Icon	Uses Nanoscope control software, including PeakForce Quantitative Nanomechanical Mapping (PF-QNM), FastForce Volume (FFV), and Point-and-Shoot Ramping experimental workspaces
AtomicJ	American Institute of Physics	https://doi.org/10.1063/1.4881683	Flexible, powerful, free open source Java-based force curve analysis software package. Supports numerous contact mechanic models, such as Hertz, Sneddon DMT, JKR, Maugis, and cone or pyramid (including blunt and truncated). Also includes a variety of initial contact point estimation methods to choose from. Supports batch processing of data and subsequent statistical analysis (e.g., averages, standard deviations, histograms, goodness of fit, etc.). Literature citation is: P. Hermanowicz, M. Sarna, K. Burda, and H. Gabry, “AtomicJ: An open source software for analysis of force curves” Rev. Sci. Instrum. 85: 063703 (2014), https://doi.org/10.1063/1.4881683
Buffer solution (PBS)	Fisher Chemical (NaCl), Sigma Aldrich (KCl), Fisher BioReagents (Na2HPO4 and KH2PO4)	S271 (>99% purity NaCl), P9541 (>99% purity KCl), BP332(>99% purity Na2HPO4), BP362 (>99% purity KH2PO4)	Phosphate buffered saline (PBS) was prepared in the laboratory as an aqueous solution consisting of 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.8 mM KH2PO4 dissolved in ultrapure water. Reagents were measured out using an analytical balance, and glassware was cleaned with soap and water followed by autoclaving immediately prior to use.
Chloroform
Diamond tip AFM probe	Bruker	PDNISP	Pre-mounted factory-calibrated cube corner diamond (E = 1140 GPa) tip AFM probe (nominal R = 40 nm) with a stainless steel cantilever (nominal k = 225 N/m, f0 = 50 kHz). Spring constant is measured at the factory (k = 256 N/m for the probe, Serial #13435414, used here) and calibration data (including AFM images of indents showing probe geometry) is provided with the probe.
Diamond ultramicrotome blade	Diatome	Ultra 35°	2.1 mm width. Also used a standard glass blade for intial rough cut of sample surface before transitioning to diamond blade for final surface preparation
Epoxy	Gorilla Glue	26853-31-6	Epoxy resin and hardner were mixed in a 1:1 ratio, a small drop was placed on a stainless steel sample puck (Ted Pella), and V1 grade muscovite mica (Ted Pella) was attached to create an atomically flat surface for preparation of phospholipid membranes.
Ethanol
LR white resin, medium grade (catalyzed)	Electron Microscopy Sciences	14381	500 mL bottle, Lot #150629
Mesenchymal stem cells (MSCs)	N/A	N/A	MSCs for nanomechanical studies were primary cells harvested from 8-10 week old male C57BL/6 mice as described in Goelzer, M. et al. "Lamin A/C Is Dispensable to Mechanical Repression of Adipogenesis" Int J Mol Sci 22: 6580 (2021) doi:10.3390/ijms22126580 and Peister, A. et al. "Adult stem cells from bone marrow (MSCs) isolated from different strains of inbred mice vary in surface epitopes, rates of proliferation, and differentiation potential" Blood 103: 1662-1668 (2004), doi:10.1182/blood-2003-09-3070.
Modulus standards	Bruker	PFQNM-SMPKIT-12M	Used HOPG (E = 18 GPa) and PS (E = 2.7 GPa). Also contains 2x PDMS (Tack 0, E = 2.5 MPa; Tack 4, E = 3.5 MPa), PS-LDPE (E = 2.0/0.2 GPa), fused silica (E = 72.9 GPa), sapphire (E - 345 GPa), and tip characterization (titanium roughness) sample. All samples come pre-mounted on a 12 mm diameter steel disc (sample puck).
Muscovite mica	Ted Pella	50-12	12 mm diameter, V1 grade muscovite mica
Nanscope Analysis	Bruker	Version 2.0	Free AFM image processing and analysis software package, but designed for, and proprietary/limited to Bruker AFMs; similar functionality is available from free, platform-independent AFM image processing and analysis software packages such as Gwyddion, WSxM, and others. Has built-in capabilities for force curve analysis, but AtomicJ is more flexible/full featured (e.g., more built-in contact mechanics models to choose from, statistical analysis of force curve fitting results, etc.) for force curve analysis and handles batch processing of force curves.
Phospholipids: POPC, Cholesterol (ovine)	Avanti Polar Lipids	POPC: CAS # 26853-31-6, Cholesterol: CAS # 57-88-5	POPC lipid dissolved in chloroform (25 mg/mL) was obtained from vendor and used without further purification. Cholesterol powder from the same vendor was dissolved in chloroform (20 mg/mL).
Probe holder (fluid, lipid bilayers)	Bruker	MTFML-V2	Specific to the particular AFM used; MTFML-V2 is a glass probe holder for scanning in fluid on a MultiMode AFM.
Probe holder (fluid, MSCs)	Bruker	FastScan Bio Z-scanner	Used with Dimension FastScan head (XY flexure scanners). Serial number MXYPOM5-1B154.
Probe holder (standard, ambient)	Bruker	DAFMCH	Specific to the particular AFM used; DAFMCH is the standard contact and tapping mode probe holder for the Dimension Icon AFM, suitable for nanoindentation (PF-QNM, FFV, and point-and-shoot ramping)
Sample Puck	Ted Pella	16218	Product number is for 15 mm diameter stainless steel sample puck. Also available in 6 mm, 10 mm, 12 mm, and 20 mm diameters at https://www.tedpella.com/AFM_html/AFM.aspx#anchor842459
Sapphire substrate	Bruker	PFQNM-SMPKIT-12M	Extremely hard surface (E = 345 GPa) for measuring deflection sensitivity of probes (want all of the deflection to come from the probe, not the substrate). Part of the PF-QNM/modulus standards kit.
Scanning electron microscope	Hitachi	S-3400N-II	Located at Boise State. Used to perform co-localized SEM/EDS on all samples except additively manufactured (AM) Ti-6Al-4V.
Silicon AFM probes (standard)	NuNano	Scout 350	Standard tapping mode silicon probe with reflective aluminum backside coating; k = 42 N/m (nominal), f0 = 350 kHz. Nominal R = 5 nm. Also available uncoated or with reflective gold backside coating. Probes with similar specifications are available from other manufacturers (e.g., Bruker TESPA-V2).
Silicon AFM probes (stiff)	Bruker	RTESPA-525, RTESPA-525-30	Rotated tip etched silicon probes with reflective aluminum backside coating; k = 200 N/m (nominal), f0 = 525 kHz. Nominal R = 8 nm for RTESPA-525, R = 30 nm for RTESPA-525-30. Spring constant of each RTESPA-525-30 is measured individually at the factory via laser Doppler vibrometry and supplied with the probe.
Silicon carbide grit paper (abrasive discs)	Allied	50-10005	120 grit
Silicon nitride AFM probes (soft, large radius hemispherical tip)	Bruker	MLCT-SPH-5UM, MLCT-SPH-5UM-DC	Also MLCT-SPH-1UM-DC. New product line of factory-calibrated (probe radius and spring constants of all cantilevers) large radius (R = 1 or 5 mm) hemispherical tip (at the end of a 23 mm long cylindrical shaft) probes. DC = drift compensation coating. 6 cantilevers/probe (A-F). Nominal spring constants: A, k = 0.07 N/m; B, k = 0.02 N/m; C, k = 0.01 N/m; D, k = 0.03 N/m; E, k = 0.1 N/m; F, k = 0.6 N/m.
Silicon nitride AFM probes (soft, medium sharp tip)	Bruker	DNP	4 cantilevers/probe (A-d). Nominal spring constants: A, k = 0.35 N/m; B, k = 0.12 N/m; C, k = 0.24 N/m; D, k = 0.06 N/m. Nominal radii of curvature, R = 10 nm.
Silicon nitride AFM probes (soft, sharp tip)	Bruker	ScanAsyst-Air	Nominal values: resonance frequency, f0 = 70 kHz; spring constant, k = 0.4 N/m; radius of curvature, R = 2 nm. Designed for force curve based AFM imaging.
Superglue	Henkel	Loctite 495	Cyanoacrylate based instant adhesive. Lots of roughly equivalent products are readily available.
Syringe pump	New Era Pump Systems	NE1000US	One channel syringe pump system with infusion and withdrawal capacity
Tip characterization standard	Bruker	PFQNM-SMPKIT-12M	Titanium (Ti) roughness standard. Part of the PF-QNM/modulus standards kit.
Ultrahigh purity nitrogen (UHP N2), 99.999%	Norco	SPG TUHPNI - T	T size compressed gas cylinder of ultrahigh purity (99.999%) nitrogen for drying samples
Ultramicrotome	Leica	EM UC6	Equipped with a glass blade (standard, for intial sample preparation) and a diamond blade (for final preparation)
Ultrapure water	Thermo Fisher	Barnstead Nanopure Model 7146	Model has been discontinued, but equivalent products are available. Produces ≥18.2 MΩ*cm ultrapure water with 1-5 ppb TOC (total organic content), per inline UV monitoring. Includes 0.2 µm particulate filter, ion exchange columns, and UV oxidation chamber.
Variable Speed Grinder	Buehler	EcoMet 3000	Used with silicon carbide grit papers during hand polishing.
Vibration isolation table (active)	Herzan	TS-140	Used with Bruker MultiMode AFM. Sits on a TMC 65-531 vibration isolation table. Bruker Dimension Icon AFM utilizes strictly passive vibration isolation (comes from manufacturer with custom acoustic hood, air table, and granite slab).
Vibration isolation table (passive)	TMC	65-531	35" x 30" vibration isolation table with optional air damping (disabled). Used with Bruker MultiMode AFM. Herzan TS-140 "Table Stable" active vibration control table is located on top.