Nanoindentação baseada em cantilever por microscopia de força atômica: medidas de propriedades mecânicas em nanoescala no ar e fluido

Resumo

A quantificação da área de contato e da força aplicadas por uma ponta de sonda de microscópio de força atômica (AFM) à superfície de uma amostra permite a determinação de propriedades mecânicas em nanoescala. As melhores práticas para implementar nanoindentação baseada em balil AFM em ar ou fluido em amostras moles e duras para medir módulo elástico ou outras propriedades nanomecânicas são discutidas.

Resumo

Um microscópio de força atômica (AFM) mede fundamentalmente a interação entre uma ponta de sonda AFM em nanoescala e a superfície da amostra. Se a força aplicada pela ponta da sonda e sua área de contato com a amostra puderem ser quantificadas, é possível determinar as propriedades mecânicas em nanoescala (por exemplo, elástico ou módulo de Young) da superfície a ser sondada. Um procedimento detalhado para a realização de experimentos quantitativos de nanoindentação baseados em balil AFM é fornecido aqui, com exemplos representativos de como a técnica pode ser aplicada para determinar os módulos elásticos de uma ampla variedade de tipos de amostras, variando de kPa a GPa. Estes incluem células-tronco mesenquimais vivas (CTMs) e núcleos em tampão fisiológico, seções transversais de pinheiro loblolly desidratadas embebidas em resina e xistos de Bakken de composição variável.

Além disso, a nanoindentação baseada em balil AFM é usada para sondar a força de ruptura (ou seja, força de ruptura) de bicamadas fosfolipídicas. Considerações práticas importantes, como escolha e desenvolvimento do método, seleção e calibração da sonda, identificação da região de interesse, heterogeneidade da amostra, tamanho e proporção das características, desgaste da ponta, rugosidade da superfície e análise de dados e estatísticas de medição são discutidas para auxiliar na implementação adequada da técnica. Finalmente, a co-localização de mapas nanomecânicos derivados de AFM com técnicas de microscopia eletrônica que fornecem informações adicionais sobre a composição elementar é demonstrada.

Introdução

Compreender as propriedades mecânicas dos materiais é uma das tarefas mais fundamentais e essenciais na engenharia. Para a análise das propriedades de materiais a granel, existem inúmeros métodos disponíveis para caracterizar as propriedades mecânicas de sistemas de materiais, incluindo ensaios de tração¹, ensaios de compressão² e ensaios de flexão de três ou quatro pontos³. Embora esses testes em microescala possam fornecer informações inestimáveis sobre as propriedades do material a granel, eles geralmente são conduzidos até a falha e, portanto, são destrutivos. Além disso, eles não têm a resolução espacial necessária para investigar com precisão as propriedades em micro e nanoescala de muitos sistemas materiais que são de interesse hoje, como filmes finos, materiais biológicos e nanocompósitos. Para começar a resolver alguns dos problemas dos ensaios mecânicos em larga escala, principalmente sua natureza destrutiva, foram adotados ensaios de microdureza a partir da mineralogia. A dureza é uma medida da resistência de um material à deformação plástica em condições específicas. Em geral, os testes de microdureza usam uma sonda rígida, geralmente feita de aço temperado ou diamante, para recuar em um material. A profundidade e/ou área de indentação resultante pode então ser usada para determinar a dureza. Vários métodos foram desenvolvidos, incluindo dureza Vickers⁴, Knoop⁵ e Brinell⁶ ; Cada um fornece uma medida de dureza do material em microescala, mas sob condições e definições diferentes, e como tal só produz dados que podem ser comparados com ensaios realizados sob as mesmas condições.

A nanoindentação instrumentada foi desenvolvida para melhorar os valores relativos obtidos através dos vários métodos de ensaio de microdureza, melhorar a resolução espacial possível para a análise de propriedades mecânicas e permitir a análise de filmes finos. É importante ressaltar que, utilizando o método desenvolvido pela primeira vez por Oliver e Pharr⁷, o módulo elástico ou módulo de Young, E, de um material de amostra pode ser determinado via nanoindentação instrumentada. Além disso, empregando uma sonda piramidal nanoindenter de três lados de Berkovich (cuja função ideal da área da ponta coincide com a da sonda piramidal de quatro lados Vickers)⁸, a comparação direta entre medidas de dureza em nanoescala e em microescala mais tradicionais pode ser feita. Com o crescimento da popularidade do AFM, a nanoindentação baseada em balil AFM começou a receber atenção também, particularmente para medir as propriedades mecânicas de materiais mais macios. Como resultado, como descrito esquematicamente na Figura 1, as duas técnicas mais comumente empregadas atualmente para interrogar e quantificar propriedades mecânicas em nanoescala são a nanoindentação instrumentada (Figura 1A) e a nanoindentação baseada em balil AFM (Figura 1B)⁹, esta última o foco deste trabalho.

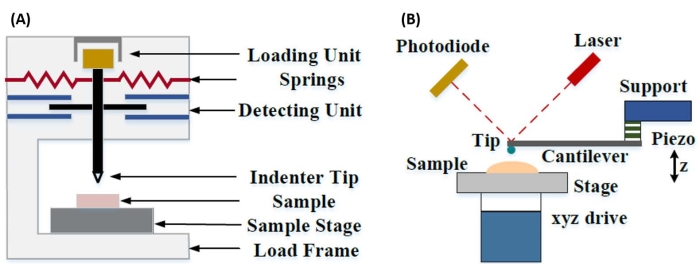
Figura 1: Comparação de sistemas de nanoindentação instrumentados e baseados em balanço. Diagramas esquemáticos descrevendo sistemas típicos para condução de (A) nanoindentação instrumentada e (B) nanoindentação baseada em balil AFM. Esse valor foi modificado de Qian et ^al.51. Abreviação: AFM = microscopia de força atômica. Clique aqui para ver uma versão maior desta figura.

Tanto a nanoindentação instrumentada quanto a nanoindentação baseada em balil AFM empregam uma sonda rígida para deformar uma superfície de amostra de interesse e monitorar a força e o deslocamento resultantes em função do tempo. Normalmente, o perfil de deslocamento de carga (ou seja, força) ou (Z-piezo) desejado é especificado pelo usuário através da interface do software e controlado diretamente pelo instrumento, enquanto o outro parâmetro é medido. A propriedade mecânica mais frequentemente obtida a partir de experimentos de nanoindentação é o módulo de elasticidade (E), também conhecido como módulo de Young, que possui unidades de pressão. O módulo de elasticidade de um material é uma propriedade fundamental relacionada à rigidez de aderência e é definido como a razão entre a tensão de tração ou compressão (σ, a força aplicada por unidade de área) e a deformação axial (ε, a deformação proporcional ao longo do eixo de indentação) durante a deformação elástica (isto é, reversível ou temporária) antes do início da deformação plástica (equação [1]):

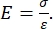(1º)

Deve-se notar que, como muitos materiais (especialmente tecidos biológicos) são de fato viscoelásticos, na realidade, o módulo (dinâmico ou complexo) consiste em componentes elásticos (armazenamento, em fase) e viscosos (perda, fora de fase). Na prática real, o que é medido em um experimento de nanoindentação é o módulo reduzido, E *, que está relacionado ao verdadeiro módulo de interesse da amostra, E, como mostrado na equação (2):

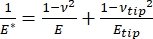(2º)

Onde E_ponta e _{ν são} o módulo elástico e a razão de Poisson, respectivamente, da ponta nanoindenter, e ν é a razão de Poisson estimada da amostra. A razão de Poisson é a razão negativa da deformação transversal para axial e, portanto, indica o grau de alongamento transversal de uma amostra ao ser submetida à deformação axial (por exemplo, durante o carregamento de nanoindentação), como mostrado na equação (3):

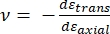(3º)

A conversão do módulo reduzido para o módulo real é necessária porque a) parte da deformação axial transmitida pela ponta do indenter pode ser convertida em deformação transversal (isto é, a amostra pode deformar via expansão ou contração perpendicular à direção do carregamento), e b) a ponta do indenter não é infinitamente dura e, portanto, o ato de recuar a amostra resulta em alguma (pequena) quantidade de deformação da ponta. Note que no caso em que a ponta E >> E (ou seja, a _ponta indenter é muito mais dura do que a amostra, o que geralmente é verdade quando se usa uma sonda de diamante), a relação entre o módulo de amostra reduzido e real simplifica muito para E ≈ E*(1 - v²). Enquanto a nanoindentação instrumentada é superior em termos de caracterização precisa da força e faixa dinâmica, a nanoindentação baseada em balil AFM é mais rápida, fornece ordens de magnitude maior sensibilidade à força e ao deslocamento, permite imagens de maior resolução e melhor localização de recuo, e pode sondar simultaneamente propriedades magnéticas e elétricas em nanoescala⁹. Em particular, a nanoindentação baseada em balanço AFM é superior para a quantificação de propriedades mecânicas na escala nanométrica de materiais moles (por exemplo, polímeros, géis, bicamadas lipídicas e células ou outros materiais biológicos), filmes extremamente finos (sub-μm) (onde os efeitos do substrato podem entrar em jogo dependendo da profundidade de indentação)^10,11 e materiais bidimensionais (2D) suspensos12,13,14, como o grafeno^15,16, mica¹⁷, nitreto de boro hexagonal (h-BN)18 ou dicalcogênios de metais de transição (TMDCs; por exemplo, MoS₂)¹⁹. Isso se deve à sua requintada sensibilidade à força (sub-nN) e ao deslocamento (sub-nm), que é importante para determinar com precisão o ponto de contato inicial e permanecer dentro da região de deformação elástica.

Na nanoindentação baseada em balil AFM, o deslocamento de uma sonda AFM em direção à superfície da amostra é acionado por um elemento piezoelétrico calibrado (Figura 1B), com o cantilever flexível eventualmente dobrando devido à força resistiva experimentada ao entrar em contato com a superfície da amostra. Esta flexão ou deflexão do cantilever é tipicamente monitorada refletindo um laser na parte de trás do cantilever e em um fotodetector (detector sensível à posição [PSD]). Aliado ao conhecimento da rigidez do cantilever (em nN/nm) e da sensibilidade à deflexão (em nm/V), é possível converter essa deflexão medida do cantilever (em V) na força (em nN) aplicada à amostra. Após o contato, a diferença entre o movimento Z-piezo e a deflexão do cantilever produz a profundidade de indentação da amostra. Combinado com o conhecimento da função de área de ponta, isso permite o cálculo da área de contato ponta-amostra. A inclinação das porções em contato das curvas de força-distância ou força-deslocamento (F-D) resultantes pode então ser ajustada usando um modelo de mecânica de contato apropriado (veja a seção Análise de Dados da discussão) para determinar as propriedades nanomecânicas da amostra. Embora a nanoindentação baseada em baltilever AFM possua algumas vantagens distintas sobre a nanoindentação instrumentada, como descrito acima, ela também apresenta vários desafios práticos de implementação, como calibração, desgaste da ponta e análise de dados, que serão discutidos aqui. Outra desvantagem potencial da nanoindentação baseada em balil AFM é a suposição de elasticidade linear, já que o raio de contato e as profundidades de indentação precisam ser muito menores do que o raio de indenter, o que pode ser difícil de alcançar quando se trabalha com sondas AFM em nanoescala e/ou amostras exibindo rugosidade superficial significativa.

Tradicionalmente, a nanoindentação tem sido limitada a locais individuais ou pequenos experimentos de recuo de grade, em que um local desejado (ou seja, região de interesse [ROI]) é selecionado e um único recuo controlado, vários recuos em um único local separados por algum tempo de espera e/ou uma grade grosseira de recuos são realizados a uma taxa da ordem de Hz. No entanto, avanços recentes no AFM permitem a aquisição simultânea de propriedades mecânicas e topografia através da utilização de modos de imagem baseados em curvas de força de alta velocidade (referidos por vários nomes comerciais dependendo do fabricante do sistema), em que as curvas de força são conduzidas a uma taxa de kHz sob controle de carga, com a força máxima da ponta-amostra utilizada como o setpoint da imagem. Métodos point-and-shoot também foram desenvolvidos, permitindo a aquisição de uma imagem de topografia AFM seguida de subsequente nanoindentação seletiva em pontos de interesse dentro da imagem, proporcionando controle espacial em nanoescala sobre a localização da nanoindentação. Embora não seja o foco principal deste trabalho, exemplos específicos de aplicação selecionados de imagens baseadas em curva de força e nanoindentação baseada em cantilever point-and-shoot são apresentados nos resultados representativos e podem ser usados em conjunto com o protocolo descrito abaixo, se disponíveis na plataforma AFM específica empregada. Especificamente, este trabalho descreve um protocolo generalizado para a implementação prática de nanoindentação baseada em baltil AFM em qualquer sistema AFM capaz e fornece quatro exemplos de casos de uso (dois no ar, dois no fluido) da técnica, incluindo resultados representativos e uma discussão aprofundada das nuances, desafios e considerações importantes para empregar a técnica com sucesso.

Protocolo

NOTA: Devido à grande variedade de AFMs disponíveis comercialmente e à diversidade de tipos de amostra e aplicações que existem para nanoindentação baseada em cantilever, o protocolo a seguir é intencionalmente projetado para ser relativamente geral por natureza, concentrando-se nas etapas compartilhadas necessárias para todos os experimentos de nanoindentação baseados em cantilever, independentemente do instrumento ou fabricante. Por causa disso, os autores supõem que o leitor possua pelo menos familiaridade básica com a operação do instrumento específico escolhido para a realização da nanoindentação baseada em cantilever. No entanto, além do protocolo geral descrito abaixo, um procedimento operacional padrão (POP) detalhado passo a passo específico para o AFM e o software usado aqui (veja Tabela de Materiais), focado na nanoindentação baseada em cantilever de amostras em fluido, está incluído como Material Suplementar.

1. Preparação da amostra e configuração do instrumento

1. Prepare a amostra de forma a minimizar a rugosidade superficial (idealmente em escala nanométrica, ~10x menor que a profundidade de indentação pretendida) e a contaminação sem alterar as propriedades mecânicas da(s) área(s) de interesse.
2. Selecione uma sonda AFM apropriada para nanoindentação da amostra pretendida com base no meio (ou seja, ar ou fluido), módulo esperado, topografia da amostra e tamanhos de características relevantes (consulte as considerações de seleção de sonda na discussão). Coloque a sonda no suporte da sonda (consulte Tabela de Materiais) e conecte o suporte da sonda à cabeça de varredura do AFM.
3. Selecione um modo de nanoindentação apropriado no software AFM que permita ao usuário o controle de rampas individuais (ou seja, curvas de deslocamento de força).
   NOTA: O modo específico será diferente entre diferentes fabricantes de AFM e instrumentos individuais (consulte o SOP fornecido no Material Suplementar para obter mais detalhes e um exemplo específico).
4. Alinhe o laser na parte de trás do cantilever da sonda, em frente ao local da ponta da sonda e no PSD.
   NOTA: Veja o exemplo de aplicação de células-tronco mesenquimais para obter mais detalhes sobre considerações importantes ao alinhar o laser e conduzir nanoindentação em fluido, em particular, evitando detritos flutuantes e/ou bolhas de ar, que podem espalhar ou refratar o feixe. A óptica AFM também pode precisar ser ajustada para compensar o índice de refração do fluido e evitar a colisão da sonda ao acoplar a superfície.
   1. Centralize o ponto do feixe de laser na parte posterior do cantiléver, maximizando a tensão de soma (Figura 2A).
   2. Centralize o ponto de feixe de laser refletido no PSD ajustando os sinais de deflexão X e Y (isto é, horizontal e vertical) para que fiquem o mais próximo possível de zero (Figura 2A), fornecendo assim a faixa de deflexão máxima detectável para produzir uma tensão de saída proporcional à deflexão do cantiléver.
5. Se não tiver certeza da topografia da amostra, rugosidade da superfície e/ou densidade da superfície (no caso de flocos ou partículas), realize uma varredura de levantamento topográfico AFM antes de qualquer experimento de nanoindentação para confirmar a adequação da amostra, conforme descrito na etapa 1.1 e na parte de preparação da amostra da discussão.

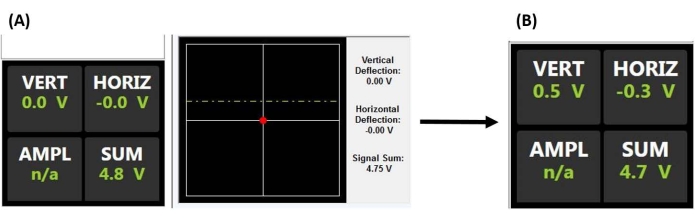
Figura 2: Monitor do detector sensível à posição. (A) Visor PSD indicando um laser devidamente alinhado refletindo na parte traseira do cantilever da sonda e no centro do PSD (como evidenciado pela tensão de soma grande e ausência de deflexão vertical ou horizontal) antes de acoplar na superfície da amostra (ou seja, sonda fora de contato com a amostra). (B) A tensão de deflexão vertical aumenta quando o cantilever é desviado (por exemplo, quando a sonda entra em contato com a amostra). Abreviações: PSD = detector sensível à posição; VERT = vertical; HORIZ = horizontal; AMPL = amplitude; n/d = não aplicável. Clique aqui para ver uma versão maior desta figura.

2. Calibração da sonda

NOTA: Três valores são necessários para quantificar as propriedades mecânicas de uma amostra usando os dados da curva F-D coletados durante a nanoindentação baseada em cantilever: a sensibilidade à deflexão (DS) do sistema cantilever/PSD (nm/V ou V/nm), a constante da mola cantilever (nN/nm) e a área de contato da sonda, frequentemente expressa em termos do raio efetivo da ponta da sonda (nm) em uma dada profundidade de recuo menor que o raio da sonda no caso de uma sonda esférica ponta.

1. Calibrar o DS do sistema sonda/AFM rampando sobre um material extremamente duro (por exemplo, safira, E = 345 GPa) de modo que a deformação da amostra seja minimizada e, assim, o movimento Z medido do piezo após o início do contato ponta-amostra seja convertido apenas em deflexão do cantilever.
   NOTA: A calibração do DS deve ser realizada nas mesmas condições que os experimentos de nanoindentação planejados (ou seja, temperatura, meio, etc.) para refletir com precisão o DS do sistema durante os experimentos. Um longo período de aquecimento do laser (30 min) pode ser necessário para a máxima precisão, a fim de permitir que o equilíbrio térmico seja alcançado e a potência de saída do laser estável e a estabilidade do ponto sejam estabelecidas. O DS deve ser remedido toda vez que o laser é realinhado, mesmo que a mesma sonda seja usada, pois o DS depende da intensidade e posição do laser no cantilever, bem como da qualidade da reflexão da sonda (ou seja, a degradação do revestimento traseiro da sonda afetará o DS) e da sensibilidade do PSD²⁰.
   1. Configure e execute os recuos de calibração do DS na safira para obter aproximadamente a mesma deflexão da sonda (em V ou nm) que os recuos de amostra planejados, uma vez que o deslocamento medido é uma função do ângulo de deflexão da ponta e torna-se não linear para grandes deflexões.
   2. Determinar o DS (em nm/V), ou, alternativamente, a sensibilidade inversa da alavanca óptica (em V/nm), a partir da inclinação da porção linear do regime de contato após o ponto de contato inicial na curva F-D resultante, como mostrado na Figura 3A.
   3. Repita a rampa pelo menos 5x, registrando cada valor de DS. Use a média dos valores para máxima precisão. Se o desvio padrão relativo (RSD) das medidas exceder ~1%, remeça o DS, pois às vezes as primeiras curvas F-D não são ideais devido à introdução inicial de forças adesivas.
   4. Se a constante de mola do cantilever da sonda, k, não for calibrada de fábrica (por exemplo, via vibrometria Doppler a laser [LDV]), calibre a constante da mola.
      NOTA: O método de ajuste térmico é ideal para balanços relativamente macios com k < 10 N/m (veja a seção constante de mola da discussão para obter uma lista e descrição de métodos alternativos, particularmente para balanços rígidos com k > 10 N/m). Como mostrado na Figura 3B, C, o ajuste térmico é normalmente integrado ao software de controle AFM.
2. Se a sonda não vier com uma medição de raio de ponta calibrada de fábrica (por exemplo, por meio de imagens de microscópio eletrônico de varredura [MEV]), meça o raio efetivo da ponta, R.
   NOTA: Existem dois métodos comuns para medir o raio da ponta (veja a seção de discussão correspondente), mas o mais comum para pontas de sonda em escala nanométrica é o método de reconstrução de ponta cega (BTR), que utiliza um padrão de rugosidade (consulte Tabela de Materiais) contendo inúmeras características extremamente nítidas (sub-nm) que servem para efetivamente obter imagens da ponta, em vez da imagem da ponta da amostra.
   1. Se empregar o método BTR, imagine a amostra de rugosidade (caracterização da ponta) usando uma taxa de varredura lenta (<0,5 Hz) e altos ganhos de feedback para ajudar a otimizar o rastreamento das características muito nítidas. Escolha um tamanho de imagem e densidade de pixels (resolução) com base no raio de ponta esperado (por exemplo, uma imagem de 1024 x 1024 pixels de uma área de 3 μm x 3 μm terá resolução lateral de ~3 nm).
   2. Use o software de análise de imagens AFM (consulte Tabela de Materiais) para modelar a ponta da sonda e estimar seu raio final e diâmetro efetivo da ponta na profundidade de recuo esperada da amostra, como mostrado na Figura 3D-F.
3. Ao concluir a calibração da sonda, insira os valores de DS, k e R no software do instrumento, como mostra a Figura 4A.
   1. Insira uma estimativa da razão de Poisson da amostra, ν, para permitir a conversão do módulo reduzido medido para o módulo de amostra real⁹. Se empregarmos um modelo de mecânica de contato cônico ou conisférico baseado na forma da ponta e na profundidade de indentação, também é necessário inserir o meio ângulo da ponta (Figura 4C).
      NOTA: O módulo é relativamente insensível a pequenos erros ou incertezas na razão de Poisson estimada. Uma estimativa de ν = 0,2-0,3 é um bom ponto de partida para muitos materiais²¹.

Figura 3: Calibração da sonda. (A) Determinação da sensibilidade à deflexão. Resultado de uma medição representativa da sensibilidade à deflexão realizada em um substrato de safira (E = 345 GPa) para uma sonda de modo de rosca padrão (k nominal = 42 N/m; ver Tabela de Materiais) com um revestimento de alumínio traseiro refletivo. São mostradas as curvas de aproximação medida (traço azul) e retração ou retirada (traço vermelho). A sensibilidade de deflexão medida de 59,16 nm/V foi determinada pelo ajuste da curva de aproximação entre os pontos de encaixe e virada de volta, conforme indicado pela região entre as linhas vermelhas pontilhadas verticais. A região de deflexão negativa evidente na curva de retração/retirada antes do arrancamento da superfície é indicativa de adesão ponta-amostra. (B,C) Sintonia térmica. Espectros representativos de ruído térmico de cantilever (traços azuis) com ajustes correspondentes (traços vermelhos) para duas sondas diferentes. (B) Configuração de ajuste térmico e parâmetros de ajuste para uma sonda de imagem AFM baseada em curva de força padrão (ver Tabela de Materiais) com sua constante nominal de mola k = 0,4 N/m usada como palpite inicial. O ajuste do espectro de ruído térmico do cantilever produz uma frequência de ressonância fundamental de f 0 = 79,8 kHz, que está em concordância razoavelmente boa com o valor nominal de f₀ = 70 kHz. O fator Q medido é 58,1. A qualidade do ajuste (R² = 0,99) é baseada na concordância do ajuste com os dados entre as duas linhas vermelhas tracejadas verticais. Observe que é importante conhecer e inserir a temperatura ambiente e a sensibilidade à deflexão para obter resultados precisos. (C) Espectro de ruído térmico do cantilever e ajuste correspondente (isto é, sintonia térmica) com a constante de mola calculada resultante k = 0,105 N/m para um cantilever extremamente macio usado para realizar medições nanomecânicas em células vivas e núcleos isolados. Observe a frequência de ressonância natural significativamente menor de ~2-3 kHz. (D-F) Reconstrução de ponta cega. Fluxo de trabalho representativo de reconstrução de ponta cega para uma sonda de ponta de diamante (R nominal = 40 nm; ver Tabela de Materiais). (D) Imagem de 5 μm x 5 μm de uma amostra de caracterização da ponta que consiste em uma série de pontas de titânio extremamente nítidas (sub-nm) que servem para obter imagens da ponta da sonda AFM. (E) Modelo resultante reconstruído (imagem de altura invertida) da ponta da sonda. (F) Resultados do ajuste da reconstrução da ponta cega, incluindo um raio final estimado de R = 29 nm e diâmetro efetivo da ponta de 40 nm a uma altura selecionada pelo usuário de 8 nm (ou seja, profundidade de recuo << R) a partir do ápice da ponta, calculados convertendo a área de contato ponta-amostra nessa altura em um diâmetro efetivo assumindo um perfil circular (ou seja, A = πr 2 = π(d/2)²) para uso com modelos de mecânica de contato esférica. Abreviações: AFM = microscopia de força atômica; ETD = diâmetro efetivo da ponta. Clique aqui para ver uma versão maior desta figura.

Figura 4: Entradas de interface de software. (A) Constantes de calibração da sonda. Interface do usuário do software (consulte Tabela de Materiais) para inserir a sensibilidade de deflexão medida, a constante de mola e o raio da ponta para permitir medições nanomecânicas quantitativas. A razão de Poisson da sonda e da amostra é necessária para calcular o módulo elástico ou de Young da amostra a partir das curvas de força de nanoindentação baseadas em cantilever. (B) Janela de controle de rampa. Interface de usuário do software (consulte Tabela de Materiais) para configurar experimentos de nanoindentação baseados em cantilever, organizados nos parâmetros que descrevem a rampa em si (ou seja, perfil de recuo), acionamento do instrumento (por exemplo, controle de força versus deslocamento), análise de força subsequente e limites de movimento (para melhorar a sensibilidade de medição estreitando a faixa sobre a qual o conversor A/D tem que operar no controle do Z-piezo e na leitura da deflexão PSD). (C) O meio ângulo da ponta (baseado na geometria da sonda ou na medida direta) é importante se um modelo de mecânica de contato cônico, piramidal ou conisférico (por exemplo, Sneddon) for empregado. Clique aqui para ver uma versão maior desta figura.

3. Coletar dados de deslocamento de força (F-D)

NOTA: Os valores dos parâmetros apresentados aqui (consulte a Figura 4B) podem variar dependendo da faixa de força e recuo para uma determinada amostra.

1. Navegue pela amostra sob o cabeçalho AFM e envolva-se na região de interesse desejada.
   1. Monitorar o sinal de deflexão vertical (Figura 2B) ou executar uma pequena rampa inicial (~50-200 nm) (Figura 4B) para verificar se a ponta e a amostra estão em contato (ver Figura 5A).
   2. Ajuste a posição da cabeça do AFM ligeiramente para cima (em passos correspondentes a ~50% do tamanho total da rampa) e rampa novamente. Repetir até que a ponta e a amostra estejam fora de contato, como evidenciado por uma rampa quase plana (Figura 5B) e mínima deflexão vertical do cantilever (Figura 2A).
   3. Uma vez que nenhuma interação óbvia ponta-amostra esteja presente (compare a Figura 2A e a Figura 2B), diminua a cabeça do AFM em uma quantidade correspondente a ~50%-100% do tamanho da rampa para garantir que a ponta da sonda não colida com a amostra enquanto move manualmente a cabeça do AFM. Rampa novamente, repetindo-se até que se observe uma boa curva (Figura 5D) ou uma curva semelhante à Figura 5C. Neste último caso, execute um pequeno ajuste adicional de abaixamento da cabeça do AFM igual a ~20%-50% do tamanho da rampa para obter um bom contato e uma curva de força semelhante à mostrada na Figura 5D.
2. Ajuste os parâmetros da rampa (conforme descrito abaixo e mostrado em Figura 4B) para otimizar o instrumento, a sonda e a amostra, e obter rampas semelhantes às mostradas em Figura 5D.
   1. Selecione um tamanho de rampa apropriado (ou seja, movimento Z-piezo total através de um ciclo de rampa) dependendo da amostra (por exemplo, espessura, módulo esperado, rugosidade superficial) e da profundidade de indentação desejada.
      NOTA: Para amostras mais rígidas, é provável que ocorra menos deformação da amostra (e, portanto, mais deflexão da sonda para um dado movimento Z-piezo), de modo que o tamanho da rampa geralmente pode ser menor do que para amostras mais macias. Os tamanhos típicos de rampa para amostras rígidas e cantilevers podem ser de dezenas de nm, enquanto para amostras macias e cantilevers as rampas podem ser de centenas de nm a alguns μm de tamanho; Exemplos específicos de aplicação selecionados são apresentados na seção Resultados representativos. Observe que os tamanhos mínimo e máximo possível de rampa dependem do instrumento.
   2. Selecione uma taxa de rampa apropriada (1 Hz é um bom ponto de partida para a maioria das amostras).
      NOTA: A taxa de rampa pode ser limitada por velocidades/larguras de banda eletrônicas de controle e/ou detecção. Em combinação com o tamanho da rampa, a taxa de rampa determina a velocidade da ponta. A velocidade da ponta é particularmente importante de ser considerada ao recuar materiais moles onde efeitos viscoelásticos podem causar artefatos de histerese ^9,22.
   3. Escolha se deseja empregar uma rampa acionada (com carga controlada) ou não acionada (com deslocamento controlado).
      NOTA: Em uma rampa acionada, o sistema abordará a amostra em etapas definidas pelo usuário (com base no tamanho da rampa e resolução ou número de pontos de dados) até que o limite de gatilho desejado (ou seja, força de setpoint ou deflexão de cantilever) seja detectado, momento em que o sistema se retrairá para sua posição original e exibirá a curva F-D. Em uma rampa não acionada, o sistema simplesmente estende o Z-piezo a distância especificada pelo tamanho da rampa definido pelo usuário e exibe a curva F-D medida. As rampas acionadas são preferidas para a maioria dos casos de uso, mas as rampas não acionadas podem ser úteis ao investigar materiais macios que não exibem um ponto de contato nítido e facilmente identificável.
      1. Se uma rampa acionada for escolhida, defina o limite de gatilho (força máxima permitida definida pelo usuário ou deflexão da rampa) para resultar no recuo desejado na amostra.
         NOTA: O uso de um limite de gatilho significa que uma rampa pode terminar (ou seja, a sonda pode começar a se retrair) antes de atingir o tamanho total da rampa (extensão Z-piezo) especificado. Os valores podem variar de alguns nN a alguns μN, dependendo do sistema de amostra-ponta.
      2. Defina a posição da rampa para determinar a porção do alcance máximo do Z-piezo que será usada para executar a rampa. Certifique-se de que o intervalo total do tamanho da rampa não comece ou termine fora do intervalo Z-piezo máximo (veja exemplos representativos na Figura 6), caso contrário, uma parte da curva F-D não representará nenhuma medida física (ou seja, o Z-piezo será totalmente estendido ou retraído, não se movendo).
   4. Defina o número de amostras/rampa (por exemplo, 512 amostras/ rampa) para alcançar a resolução desejada da medição (ou seja, densidade de pontos da curva F-D).
      NOTA: O máximo de amostras/rampa pode ser limitado por restrições de software (tamanho do arquivo) ou hardware (por exemplo, velocidade de conversão analógica para digital [A/D], dependendo da taxa da rampa). Também é possível limitar a faixa Z-piezo ou de deflexão permitida (ver parâmetros de limites na Figura 4B) para aumentar a resolução efetiva do conversor A/D do sistema.
   5. Ajuste o X-gire para reduzir as forças de cisalhamento na amostra e na ponta, movendo simultaneamente a sonda ligeiramente na direção X (paralela ao cantilever) enquanto recua na direção Z (perpendicular ao cantilever). Use um valor para o X-girar igual ao ângulo de deslocamento do suporte da sonda em relação à superfície normal (12° é típico).
      NOTA: O X-girate é necessário porque o cantilever é montado no suporte da sonda em um pequeno ângulo em relação à superfície para permitir que o feixe de laser incidente reflita no PSD. Além disso, os ângulos frontal e traseiro da ponta da sonda podem diferir entre si (ou seja, a ponta da sonda pode ser assimétrica). Informações mais específicas podem ser obtidas de fabricantes individuais de sonda e AFM.

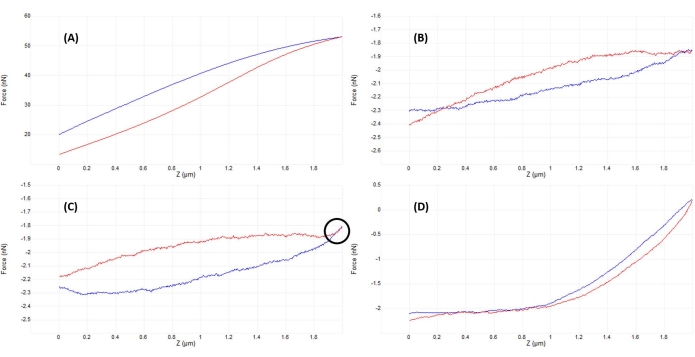
Figura 5: Otimização da separação ponta-amostra após o acoplamento para obter boas curvas de força. Exemplos sequenciais de curvas representativas de força-deslocamento obtidas durante o recuo em fluido (solução salina tamponada com fosfato) em um núcleo de células-tronco mesenquimais vivas com um cantilever de nitreto de silício macio calibrado ( k nominal = 0,04 N/m) terminando em uma ponta hemisférica de 5 μm de raio (ver Tabela de Materiais). As curvas foram obtidas no processo de acoplamento da superfície celular e otimização dos parâmetros de indentação, com abordagem de sonda mostrada em azul e retração/retirada em vermelho. (A) A ponta já está engatada e em contato com a amostra antes do início da rampa, levando a grandes deflexões e forças de cantiléver, sem linha de base plana de pré-contato. (B) Depois de mover manualmente a ponta suficientemente longe da amostra, uma rampa de 2 μm não acionada resulta em uma curva F-D que é quase plana (ou seja, praticamente nenhuma mudança na força). Em condições ambientais, a curva seria mais plana, mas em fluido, a viscosidade do meio pode causar ligeiras deflexões do cantilever da sonda durante uma rampa como visto aqui, mesmo sem contato com a superfície. (C) Após aproximar-se um pouco mais da superfície antes de iniciar a rampa, as curvas de aproximação e retração mostram um ligeiro aumento de força (aumento da inclinação) próximo ao ponto de virada da rampa (ou seja, transição da aproximação para a retirada). O sinal revelador a procurar é que as curvas de aproximação (azul) e retirada (vermelho) começam a se sobrepor (região indicada pelo círculo preto), o que é indicativo de uma interação física com a superfície. (D) Uma curva F-D ideal adquirida após otimização dos parâmetros da rampa e aproximando-se ligeiramente (~1 μm) mais próxima da superfície celular do que em C , de modo que a sonda gaste aproximadamente metade da rampa em contato com a célula, permitindo deformação suficiente para ajustar a porção de contato da curva de aproximação e determinar o módulo de elasticidade. A linha de base relativamente longa, plana e de baixo ruído torna mais fácil para o algoritmo de ajuste determinar o ponto de contato. Abreviação: F-D = força-deslocamento. Clique aqui para ver uma versão maior desta figura.

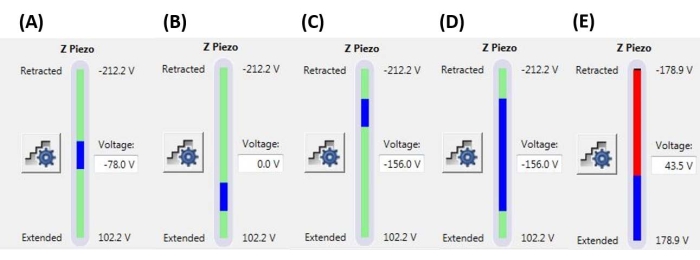
Figura 6: Tamanho e posição da rampa. Monitor Z-piezo mostrando a extensão da rampa (barra azul) em relação à faixa de movimento Z-piezo total disponível (barra verde). (A) A posição Z-piezo está próxima ao meio de sua amplitude de movimento, como indicado tanto pela barra azul estar localizada aproximadamente no meio da barra verde quanto pela tensão Z-piezo atual (-78,0 V) estar aproximadamente entre seus valores totalmente retraídos (-212,2 V) e estendidos (+102,2 V). (B) Z-piezo é estendido em relação a A, sem tensão de polarização aplicada. (C) Z-piezo é retraído em relação a A e B. (D) A posição Z-piezo é a mesma que em C em -156,0 V, mas o tamanho da rampa foi aumentado em relação a A-C para aproveitar mais da amplitude de movimento total do Z-piezo. € O tamanho da rampa é muito grande para a posição atual da rampa, resultando no Z-piezo sendo estendido até o final de sua gama. Isso fará com que a curva F-D fique plana, pois o sistema não pode estender o Z-piezo ainda mais. Abreviação: F-D = força-deslocamento. Clique aqui para ver uma versão maior desta figura.

4. Análise da curva F-D

1. Escolha um pacote de software de análise de dados apropriado. Selecione e carregue os dados a serem analisados.
   NOTA: Muitos fabricantes de AFM e programas de software de processamento de imagem AFM têm suporte incorporado para análise de curva F-D. Alternativamente, a maior flexibilidade e os recursos de um pacote dedicado de análise de curvas F-D, como o pacote de software de código aberto AtomicJ, podem ser benéficos²³, particularmente para processamento em lote e análise estatística de grandes conjuntos de dados ou implementação de modelos complexos de mecânica de contato.
2. Valores calibrados de entrada para a constante de mola, DS e raio da ponta da sonda, juntamente com estimativas do módulo de Young e razão de Poisson para a ponta da sonda (com base em sua composição de material) e a razão de Poisson da amostra.
   OBS: Se utilizar um indenter de ponta de diamante, os valores de_ponta E = 1140 GPa e ponta ν₌ 0,07 podem ser utilizados^21,24,25,26. Para uma sonda de silício padrão, a ponta E = 170 GPa e _{a ponta} ν = 0,27 podem ser tipicamente usadas, embora o módulo de silício de Young varie dependendo da orientação cristalográfica²⁷.
3. Escolha um modelo de mecânica de contato de nanoindentação apropriado para a ponta e a amostra.
   NOTA: Para os muitos modelos de ponta esférica comuns (por exemplo, Hertz, Maugis, DMT, JKR), é imperativo que a profundidade de recuo na amostra seja menor do que o raio da ponta; caso contrário, a geometria esférica da ponta da sonda dá lugar a uma forma cônica ou piramidal (Figura 4C). Para modelos cônicos (por exemplo, Sneddon²⁸) e piramidais, o meio ângulo da ponta (ou seja, o ângulo entre a parede lateral da ponta e uma linha de bissetriz perpendicular à extremidade da ponta; Figura 4C) deve ser conhecido e geralmente está disponível no fabricante da sonda. Para obter mais informações sobre modelos de mecânica de contato, consulte a seção Análise de dados do dDiscussion.
4. Execute o algoritmo de ajuste. Verificar o ajuste adequado das curvas F-D; um baixo erro residual correspondente a uma unidade próxima de R 2 média (por exemplo, R² > 0,9) é tipicamente indicativo de um bom ajuste ao modelo escolhido^29,30. Verifique pontualmente as curvas individuais para inspecionar visualmente a curva, o ajuste do modelo e os pontos de contato calculados, se desejado (por exemplo, consulte a Figura 7 e a seção Análise de dados da discussão).

Resultados

Curvas força-deslocamento
A Figura 7 mostra curvas F-D representativas e quase ideais obtidas de experimentos de nanoindentação realizados no ar em amostras de pinheiro loblolly emblocadas em resina (Figura 7A) e em fluido (solução salina tamponada com fosfato [PBS]) em núcleos de células-tronco mesenquimais (CTM) (Figura 7B). O uso de qualquer modelo de mecânica de contato depende da determinação preci...

Discussão

Preparo da amostra
Para nanoindentação no ar, os métodos de preparação comuns incluem criossecção (por exemplo, amostras de tecido), moagem e/ou polimento seguido de ultramicrotomografia (por exemplo, amostras biológicas embutidas em resina), moagem de íons ou preparação de feixe de íons focalizado (por exemplo, amostras de dureza semicondutora, porosa ou mista não passíveis de polimento), polimento mecânico ou eletroquímico (por exemplo, ligas metálicas) ou deposição de filme fino ...

Materiais

Name	Company	Catalog Number	Comments
Atomic force microscope	Bruker	Dimension Icon	Uses Nanoscope control software, including PeakForce Quantitative Nanomechanical Mapping (PF-QNM), FastForce Volume (FFV), and Point-and-Shoot Ramping experimental workspaces
AtomicJ	American Institute of Physics	https://doi.org/10.1063/1.4881683	Flexible, powerful, free open source Java-based force curve analysis software package. Supports numerous contact mechanic models, such as Hertz, Sneddon DMT, JKR, Maugis, and cone or pyramid (including blunt and truncated). Also includes a variety of initial contact point estimation methods to choose from. Supports batch processing of data and subsequent statistical analysis (e.g., averages, standard deviations, histograms, goodness of fit, etc.). Literature citation is: P. Hermanowicz, M. Sarna, K. Burda, and H. Gabry, “AtomicJ: An open source software for analysis of force curves” Rev. Sci. Instrum. 85: 063703 (2014), https://doi.org/10.1063/1.4881683
Buffer solution (PBS)	Fisher Chemical (NaCl), Sigma Aldrich (KCl), Fisher BioReagents (Na2HPO4 and KH2PO4)	S271 (>99% purity NaCl), P9541 (>99% purity KCl), BP332(>99% purity Na2HPO4), BP362 (>99% purity KH2PO4)	Phosphate buffered saline (PBS) was prepared in the laboratory as an aqueous solution consisting of 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.8 mM KH2PO4 dissolved in ultrapure water. Reagents were measured out using an analytical balance, and glassware was cleaned with soap and water followed by autoclaving immediately prior to use.
Chloroform
Diamond tip AFM probe	Bruker	PDNISP	Pre-mounted factory-calibrated cube corner diamond (E = 1140 GPa) tip AFM probe (nominal R = 40 nm) with a stainless steel cantilever (nominal k = 225 N/m, f0 = 50 kHz). Spring constant is measured at the factory (k = 256 N/m for the probe, Serial #13435414, used here) and calibration data (including AFM images of indents showing probe geometry) is provided with the probe.
Diamond ultramicrotome blade	Diatome	Ultra 35°	2.1 mm width. Also used a standard glass blade for intial rough cut of sample surface before transitioning to diamond blade for final surface preparation
Epoxy	Gorilla Glue	26853-31-6	Epoxy resin and hardner were mixed in a 1:1 ratio, a small drop was placed on a stainless steel sample puck (Ted Pella), and V1 grade muscovite mica (Ted Pella) was attached to create an atomically flat surface for preparation of phospholipid membranes.
Ethanol
LR white resin, medium grade (catalyzed)	Electron Microscopy Sciences	14381	500 mL bottle, Lot #150629
Mesenchymal stem cells (MSCs)	N/A	N/A	MSCs for nanomechanical studies were primary cells harvested from 8-10 week old male C57BL/6 mice as described in Goelzer, M. et al. "Lamin A/C Is Dispensable to Mechanical Repression of Adipogenesis" Int J Mol Sci 22: 6580 (2021) doi:10.3390/ijms22126580 and Peister, A. et al. "Adult stem cells from bone marrow (MSCs) isolated from different strains of inbred mice vary in surface epitopes, rates of proliferation, and differentiation potential" Blood 103: 1662-1668 (2004), doi:10.1182/blood-2003-09-3070.
Modulus standards	Bruker	PFQNM-SMPKIT-12M	Used HOPG (E = 18 GPa) and PS (E = 2.7 GPa). Also contains 2x PDMS (Tack 0, E = 2.5 MPa; Tack 4, E = 3.5 MPa), PS-LDPE (E = 2.0/0.2 GPa), fused silica (E = 72.9 GPa), sapphire (E - 345 GPa), and tip characterization (titanium roughness) sample. All samples come pre-mounted on a 12 mm diameter steel disc (sample puck).
Muscovite mica	Ted Pella	50-12	12 mm diameter, V1 grade muscovite mica
Nanscope Analysis	Bruker	Version 2.0	Free AFM image processing and analysis software package, but designed for, and proprietary/limited to Bruker AFMs; similar functionality is available from free, platform-independent AFM image processing and analysis software packages such as Gwyddion, WSxM, and others. Has built-in capabilities for force curve analysis, but AtomicJ is more flexible/full featured (e.g., more built-in contact mechanics models to choose from, statistical analysis of force curve fitting results, etc.) for force curve analysis and handles batch processing of force curves.
Phospholipids: POPC, Cholesterol (ovine)	Avanti Polar Lipids	POPC: CAS # 26853-31-6, Cholesterol: CAS # 57-88-5	POPC lipid dissolved in chloroform (25 mg/mL) was obtained from vendor and used without further purification. Cholesterol powder from the same vendor was dissolved in chloroform (20 mg/mL).
Probe holder (fluid, lipid bilayers)	Bruker	MTFML-V2	Specific to the particular AFM used; MTFML-V2 is a glass probe holder for scanning in fluid on a MultiMode AFM.
Probe holder (fluid, MSCs)	Bruker	FastScan Bio Z-scanner	Used with Dimension FastScan head (XY flexure scanners). Serial number MXYPOM5-1B154.
Probe holder (standard, ambient)	Bruker	DAFMCH	Specific to the particular AFM used; DAFMCH is the standard contact and tapping mode probe holder for the Dimension Icon AFM, suitable for nanoindentation (PF-QNM, FFV, and point-and-shoot ramping)
Sample Puck	Ted Pella	16218	Product number is for 15 mm diameter stainless steel sample puck. Also available in 6 mm, 10 mm, 12 mm, and 20 mm diameters at https://www.tedpella.com/AFM_html/AFM.aspx#anchor842459
Sapphire substrate	Bruker	PFQNM-SMPKIT-12M	Extremely hard surface (E = 345 GPa) for measuring deflection sensitivity of probes (want all of the deflection to come from the probe, not the substrate). Part of the PF-QNM/modulus standards kit.
Scanning electron microscope	Hitachi	S-3400N-II	Located at Boise State. Used to perform co-localized SEM/EDS on all samples except additively manufactured (AM) Ti-6Al-4V.
Silicon AFM probes (standard)	NuNano	Scout 350	Standard tapping mode silicon probe with reflective aluminum backside coating; k = 42 N/m (nominal), f0 = 350 kHz. Nominal R = 5 nm. Also available uncoated or with reflective gold backside coating. Probes with similar specifications are available from other manufacturers (e.g., Bruker TESPA-V2).
Silicon AFM probes (stiff)	Bruker	RTESPA-525, RTESPA-525-30	Rotated tip etched silicon probes with reflective aluminum backside coating; k = 200 N/m (nominal), f0 = 525 kHz. Nominal R = 8 nm for RTESPA-525, R = 30 nm for RTESPA-525-30. Spring constant of each RTESPA-525-30 is measured individually at the factory via laser Doppler vibrometry and supplied with the probe.
Silicon carbide grit paper (abrasive discs)	Allied	50-10005	120 grit
Silicon nitride AFM probes (soft, large radius hemispherical tip)	Bruker	MLCT-SPH-5UM, MLCT-SPH-5UM-DC	Also MLCT-SPH-1UM-DC. New product line of factory-calibrated (probe radius and spring constants of all cantilevers) large radius (R = 1 or 5 mm) hemispherical tip (at the end of a 23 mm long cylindrical shaft) probes. DC = drift compensation coating. 6 cantilevers/probe (A-F). Nominal spring constants: A, k = 0.07 N/m; B, k = 0.02 N/m; C, k = 0.01 N/m; D, k = 0.03 N/m; E, k = 0.1 N/m; F, k = 0.6 N/m.
Silicon nitride AFM probes (soft, medium sharp tip)	Bruker	DNP	4 cantilevers/probe (A-d). Nominal spring constants: A, k = 0.35 N/m; B, k = 0.12 N/m; C, k = 0.24 N/m; D, k = 0.06 N/m. Nominal radii of curvature, R = 10 nm.
Silicon nitride AFM probes (soft, sharp tip)	Bruker	ScanAsyst-Air	Nominal values: resonance frequency, f0 = 70 kHz; spring constant, k = 0.4 N/m; radius of curvature, R = 2 nm. Designed for force curve based AFM imaging.
Superglue	Henkel	Loctite 495	Cyanoacrylate based instant adhesive. Lots of roughly equivalent products are readily available.
Syringe pump	New Era Pump Systems	NE1000US	One channel syringe pump system with infusion and withdrawal capacity
Tip characterization standard	Bruker	PFQNM-SMPKIT-12M	Titanium (Ti) roughness standard. Part of the PF-QNM/modulus standards kit.
Ultrahigh purity nitrogen (UHP N2), 99.999%	Norco	SPG TUHPNI - T	T size compressed gas cylinder of ultrahigh purity (99.999%) nitrogen for drying samples
Ultramicrotome	Leica	EM UC6	Equipped with a glass blade (standard, for intial sample preparation) and a diamond blade (for final preparation)
Ultrapure water	Thermo Fisher	Barnstead Nanopure Model 7146	Model has been discontinued, but equivalent products are available. Produces ≥18.2 MΩ*cm ultrapure water with 1-5 ppb TOC (total organic content), per inline UV monitoring. Includes 0.2 µm particulate filter, ion exchange columns, and UV oxidation chamber.
Variable Speed Grinder	Buehler	EcoMet 3000	Used with silicon carbide grit papers during hand polishing.
Vibration isolation table (active)	Herzan	TS-140	Used with Bruker MultiMode AFM. Sits on a TMC 65-531 vibration isolation table. Bruker Dimension Icon AFM utilizes strictly passive vibration isolation (comes from manufacturer with custom acoustic hood, air table, and granite slab).
Vibration isolation table (passive)	TMC	65-531	35" x 30" vibration isolation table with optional air damping (disabled). Used with Bruker MultiMode AFM. Herzan TS-140 "Table Stable" active vibration control table is located on top.