JoVE Logo
Autoren
Kontakt

Anmelden

Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.

In diesem Artikel

  • Zusammenfassung
  • Zusammenfassung
  • Einleitung
  • Protokoll
  • Ergebnisse
  • Diskussion
  • Offenlegungen
  • Danksagungen
  • Materialien
  • Referenzen
  • Nachdrucke und Genehmigungen

Zusammenfassung

Die Kernspinresonanzspektroskopie (NMR) kann die Dynamik von Strukturproteinen rückstandsspezifisch charakterisieren. Wir bieten ein praxisorientiertes Protokoll für die Aufzeichnung von NMR 15N R1 und R2 Relaxations- und {1H}-15N heteronuklearen Overhauser Effekt (hetNOE) Experimenten, das für die Zeitskala von Pikosekunden bis Nanosekunden empfindlich ist.

Zusammenfassung

Die Kernspinresonanzspektroskopie (NMR) ermöglicht die Untersuchung von Proteinen in Lösung und bei physiologischen Temperaturen. Häufig werden entweder die Amidgruppen des Proteinrückgrats oder die Methylgruppen in Seitenketten als Reporter der Strukturdynamik in Proteinen verwendet. Eine strukturdynamische Untersuchung des Proteinrückgrats globulärer Proteine an 15N markierten und vollständig protonierten Proben funktioniert in der Regel gut für Proteine mit einem Molekulargewicht von bis zu 50 kDa. Bei Anwendung der Seitenkettendeuteration in Kombination mit der transversalen relaxationsoptimierten Spektroskopie (TROSY) kann dieser Grenzwert auf bis zu 200 kDa für globuläre Proteine und bis zu 1 MDa erweitert werden, wenn der Fokus auf den Seitenketten liegt. Bei der Untersuchung von intrinsisch ungeordneten Proteinen (IDPs) oder Proteinen mit intrinsisch ungeordneten Regionen (IDRs) gelten diese Gewichtsbeschränkungen nicht, können aber weit darüber hinausgehen. Der Grund dafür ist, dass IDPs oder IDRs, die sich durch eine hohe interne Flexibilität auszeichnen, häufig dynamisch entkoppelt sind. Verschiedene NMR-Methoden bieten atomar aufgelöste Einblicke in die Dynamik von Strukturproteinen über eine Vielzahl von Zeitskalen, von Pikosekunden bis hin zu Stunden. Standard-15-N-Relaxationsmessungen geben einen Überblick über die interne Flexibilität eines Proteins und charakterisieren die Dynamik des Proteinrückgrats auf der schnellen Zeitskala von Piko- bis Nanosekunden. In diesem Artikel wird ein praktisches Protokoll für den Aufbau und die Aufzeichnung von NMR 15N R1, R2 und heteronuklearen Overhauser-Effekt (hetNOE)-Experimenten vorgestellt. Wir zeigen beispielhafte Daten und erklären, wie man sie vor einer anspruchsvolleren Analyse einfach qualitativ interpretieren kann.

Einleitung

Die Funktion eines Proteins wird nicht nur durch seine dreidimensionale Struktur bestimmt, sondern auch durch seine strukturelle Dynamik, die seine innere Flexibilität und die strukturellen Übergänge zwischen verschiedenen Konformationen umfasst, die das Protein annehmen wird. Mit der Kernspinresonanzspektroskopie (NMR) kann die Strukturdynamik von Proteinen in Lösung 1,2,3 untersucht werden. Neuere Entwicklungen in der protonendetektierten Festkörper-NMR ermöglichen auch die Charakterisierung der Proteindynamik in einem weniger löslichen Zustand, wie z. B. einer Lipid-Doppelschichtmembran 4,5,6. In der Lösungs-NMR kann die strukturelle Dynamik des Proteinrückgrats und der Proteinseitenketten untersucht werden. Für ein globuläres Protein kann eine Strukturdynamikuntersuchung des Proteinrückgrats bis zu 50 kDa durchgeführt werden, sobald das Protein mit 15N isotopenmarkiert ist. Beim Einsatz der Seitenkettendeuteration und der transversalen relaxationsoptimierten Spektroskopie (TROSY) kann dieser Grenzwert auf bis zu 200 kDaerweitert werden 7,8. Wenn der Fokus auf der Seitenkettendynamik liegt, kann das Spektrum der zugänglichen Proteine und Komplexe auf bis zu 1 MDa erweitert werden 2,9.

Die genannten Gewichtsbeschränkungen gelten nicht für intrinsisch ungeordnete Proteine (IDPs), die häufig eine hohe intrinsische Dynamik aufweisen. Über 30% des eukaryotischen Proteoms bestehen aus IDPs oder intrinsisch ungeordneten Regionen (IDRs)10,11,12,13. Sie spielen eine zentrale Rolle in vielen zellulären Prozessen, wie z. B. der Signaltransduktion und Transkription1, und sind häufig an der intrazellulären Phasentrennung beteiligt 14,15,16,17. Binnenvertriebenen fehlt unter physiologischen Bedingungen eine gut definierte dreidimensionale (3D) native Struktur und sie haben eine schwach trichterförmige oder zerklüftete Energielandschaft17,18. Aufgrund einer geringen Hydrophobizität und einer starken elektrostatischen Abstoßung, die über das Rückgrat von IDPs oder IDRs verteilt ist, fehlt eine treibende Kraft für die Faltung zu einer starren Struktur19. IDPs nehmen häufig eine gefaltete Konformation an, wenn sie mit anderen Bindungspartnern komplexsind 10,20,21. Außerdem erweitern posttranslationale Modifikationen (PTMs) die Faltungsmöglichkeiten von IDPs oder IDRs22,23. Die Fehlfaltung von Binnenvertriebenen wurde als Ursache für verschiedene Krankheiten identifiziert, einschließlich neurodegenerativer Erkrankungen 15,24,25,26.

Binnenvertriebene und indirekte Überprüfungen weisen eine hohe interne Flexibilität auf 21,27,28. Konformationsensembles, die die Variation der atomaren Positionen und Flächenwinkel anzeigen, wurden aus Molekulardynamik-Simulationen abgeleitet und Einschränkungen aus experimentellen Datengewonnen 29,30,31,32. Aufgrund der Dynamik und der daraus resultierenden Unordnung im gefrorenen Zustand ist es aufgrund der diffusen Elektronendichte schwierig, sie mit modernsten Methoden der Strukturbiologie, wie z.B. Kryo-EM oder Röntgenkristallographie, strukturell zu charakterisieren. Auch Kristallisationsbedingungen oder Probenvorbereitungstechniken für Experimente bei kryogenen Temperaturen können sich auf den Konformationsraum auswirken, den IDPs erleben. Die Lösungs-NMR eignet sich jedoch gut für hochdynamische Proteine und eignet sich daher gut für die Untersuchung der IDPs 16,20,22,28,29,30,31,32,33,34,35,36,37,38.

Wie oben vorgestellt, bietet die Lösungs-NMR verschiedene Techniken zur Untersuchung der internen Proteindynamik über einen weiten Bereich von Zeitskalen (Abbildung 1), hauptsächlich basierend auf der Spinrelaxation 31,33,38,39,40,41,42.

Die Spinrelaxation der 15N-Kerne in den Amidgruppen des Proteinrückgrats wird durch Änderungen des Orientierungswinkels der 1 H-15N-Bindung aufgrund der internen Proteindynamik und kollektiver Bewegungen (einschließlich, falls relevant, Rotationsdiffusion) induziert.27,43,44,45,46,47,48,49,50,51. Auf Zeitskalen, die kürzer sind als die Rotationskorrelationszeit τ R (die Zeit, die das Molekül benötigt, um einen Radianten zu rotieren, auch als Gesamtkorrelationszeit bezeichnet), sind die chemische Verschiebungsanisotropie (CSA) und die dipolareKopplung (D) aktiv und werden nicht durch die Rotationsdiffusion des Proteins gemittelt. Die interne Dynamik des Proteinrückgrats, bestehend aus Variationen der Bindungswinkel, Neuorientierungen der Bindungen und Rotationstaumeln, induziert stochastische Fluktuationen des CSA und des dipolaren Kupplungstensors, was zu einer Variation des lokalen Magnetfeldes führt, was letztendlich zu einer NMR-Spinrelaxation führt 47,48,52,53. Diese Schwankungen können durch eine Gesamtkorrelationsfunktion beschrieben werden. Die Fourier-Transformation der Gesamtkorrelationsfunktion wird als spektrale Dichtefunktion bezeichnet. In der semi-klassischen Redfield-Relaxationstheorie können die NMR-Relaxationsgeschwindigkeitskonstanten durch lineare Kombinationen dieser spektralen Dichtefunktionenbeschrieben werden 54.

Backbone 15N NMR-Relaxationsexperimente, die in den frühen 1990er Jahren entwickelt wurden, umfassen 15N R1, R1ρ und {1H}-15N nukleare Overhauser-Effekt-Experimente, die empfindlich auf die Zeitskala der schnellen Pikosekunden (ps) Nanosekunden (ns) reagieren, schneller als die Rotationskorrelationszeit τR des Proteins 45,55,56,57. Um die Dynamik des Rückgrats langsamer als die Rotationskorrelationszeit τR zu charakterisieren, werden sogenannte Relaxationsdispersionsexperimente R1ρ und Carr-Purcell-Meiboom-Gill (CPMG) Experimente verwendet, die für die Dynamik von Mikrosekunden (μs) - Millisekunden (ms) 44,46,58,59,60,61 empfindlich sind. Dynamiken, die langsamer als Mikrosekunden sind, können mit 15N chemischer Austauschsättigungstransfer (CEST) NMR62, Austauschspektroskopie (EXSY, Millisekunden bis Sekunden) oder Echtzeit-NMR (Sekunden bis Stunden)63,64 erfasst werden. Der PRE-Effekt (paramagnetic relaxation enhancement) von paramagnetischen Sonden sowie von residualen dipolaren Kopplungen (RDCs) kann verwendet werden, um den gesamten Bereich der ps- bis ms-Dynamik 65,66,67,68 zu beurteilen.

figure-introduction-9477
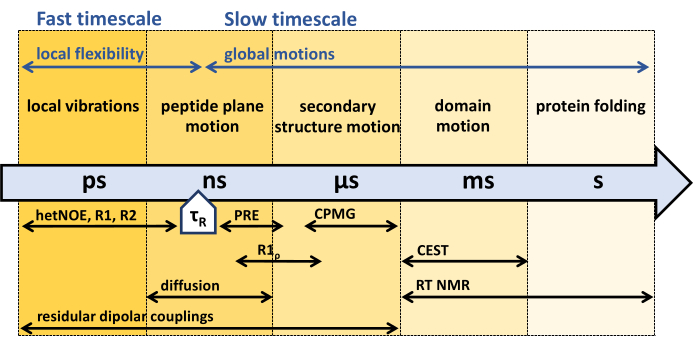
Abbildung 1: Zeitskalen der Dynamik des Proteinrückgrats und sensitives Zeitfenster verschiedener NMR-Dynamik-Experimente. Die NMR bietet eine Vielzahl von Methoden, um die Dynamik des Proteinrückgrats über einen weiten Bereich von Zeitskalen zu charakterisieren. Unterschiedliche Bewegungen, die das Proteinrückgrat erfährt, werden auf ihren jeweiligen Zeitskalen angezeigt. Die Rotationskorrelationszeit des Proteins, τR, ist die Zeit, die das Protein für eine Gesamtumdrehung (um einen Radianten) benötigt. Bewegungen, die schneller sind als die Rotationskorrelationszeit des Proteins, τR, können mit der internen Flexibilität des Proteins in Verbindung gebracht werden. Unterhalb des Pfeils sind verschiedene NMR-Experimente und deren Empfindlichkeit gegenüber den jeweiligen Zeitskalen angedeutet. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Das folgende Protokoll beschreibt den Aufbau von NMR-Relaxationsexperimenten von Lakomek et al.69 und Stief et al.70 unter Verwendung eines sensitivitätsverstärkten heteronuklearen Einzelquantenkohärenz-Detektionsschemas (HSQC). Bevor wir mit der experimentellen Umsetzung fortfahren, wird ein sehr kurzer Überblick über NMR-Spinrelaxations- und NMR-Relaxationsexperimente gegeben. Aufgrund von Größenbeschränkungen und um dieses Protokoll verständlich zu halten, muss diese Übersicht einfach (und daher unvollständig) bleiben.

Die Längs- oder Spin-Gitter-Relaxation, charakterisiert durch die T1-Zeit oder die R1 = 1/ T 1-Gangkonstante, beschreibt die Rückkehr der Magnetisierung zum Boltzmann-Gleichgewicht. Im Gleichgewicht wird die Magnetisierung entlang der Achse des äußeren Magnetfeldes ausgerichtet, das die z-Achse des Laborrahmens definiert. Spektrale Dichten bei hohen (1H) und kleinen (15N) Larmor-Frequenzen (die NMR-Resonanzfrequenzen, z. B. 600 MHz für 1H für einen 14,1-Tesla-Magneten) und lineare Kombinationen dieser Larmor-Frequenzen tragen zur 15N R1-Relaxation bei, die durch die 15N R 1-Geschwindigkeitskonstanten charakterisiert wird, die in rad·s-1 gemessen werden. Bewegungen auf Zeitskalen sind umgekehrt zu diesen Larmor-Frequenzen; Bewegungen auf der Zeitskala von Pikosekunden bis Nanosekunden tragen also zur Relaxationsratenkonstante R1 bei. Für Moleküle, die ein allgemeines Taumeln aufweisen und bei denen eine Rotationskorrelationszeit definiert werden kann, zeigt die R1 (T1)-Kurve ein Maximum (Minimum) für ωτR = 1, wobei die Rotationskorrelation τR und die Larmor-Frequenz ω des betreffenden Spins berücksichtigt werden. Wenn mehrere Larmor-Frequenzen beitragen, ist die mit der niedrigsten Frequenz die dominante, z. B. ωN im Fall von 15N R1. Das Zeitrafferregime (ωτR viel kleiner als 1) gilt für kleine Moleküle, die sehr schnell taumeln, sowie für niedrige Magnetfelder und niedrige Viskosität. Das Zeitlupenregime (ωτR viel größer als 1) gilt für größere Moleküle, die langsamer taumeln, sowie für hohe Magnetfelder und hohe Viskosität.

Kugelförmig gefaltete Proteine zeigen ein allgemeines Taumeln in Lösung, und eine Rotationskorrelationszeit kann zugeordnet werden. Das Konzept des Gesamttaumelns ist jedoch für intrinsisch ungeordnete Proteine nicht mehr gültig und unterscheidet sich häufig von der Zuweisung einer einzelnen Rotationskorrelationszeit. Hier wird die restspezifische interne Korrelationszeit kritischer.

Die beschriebene Pulssequenz zur Messung von 15N R1 Relaxationsraten (Abbildung 2) basiert auf einem sensitivitätsverstärkten HSQC-Ausleseexperiment mit einer Echo/Anti-Echo-Detektion für die Quadraturdetektion 69,70,71. Kurze Gradienten mit variabler Stärke und Länge werden für die Kohärenzselektion und eine verbesserte Wasserunterdrückung verwendet70. Während dieser Zeit entspannt sich die longitudinale Polarisation von 15N. Längere Abklingzeiten führen zu reduzierten Intensitäten in den zugehörigen 2D-Ebenen dieses Pseudo-3D-Spektrums (Verzögerungsdatenpunkte werden in der dritten Dimension aufgezeichnet). Ein Schleifenelement, das im Folgenden beschrieben wird, wird für längere Relaxationszeiten immer öfter ausgeführt. Da die kreuzkorrelierte Relaxation zwischen der 15N chemischen Verschiebungsanisotropie (CSA) und der 1H und 15N Dipolarkopplung (D) auch während der Relaxationsverzögerung aktiv ist, ist ein zentraler I-BURP-2 180°-Puls72 notwendig, der selektiv auf die Amidprotonen wirkt, um den Beitrag durch kreuzkorrelierte Relaxation neu zu fokussieren (die, wenn sie nicht neu fokussiert wird, zu verzerrten und fehlerhaften 15N R1 Geschwindigkeitskonstanten führen würde).

figure-introduction-14991
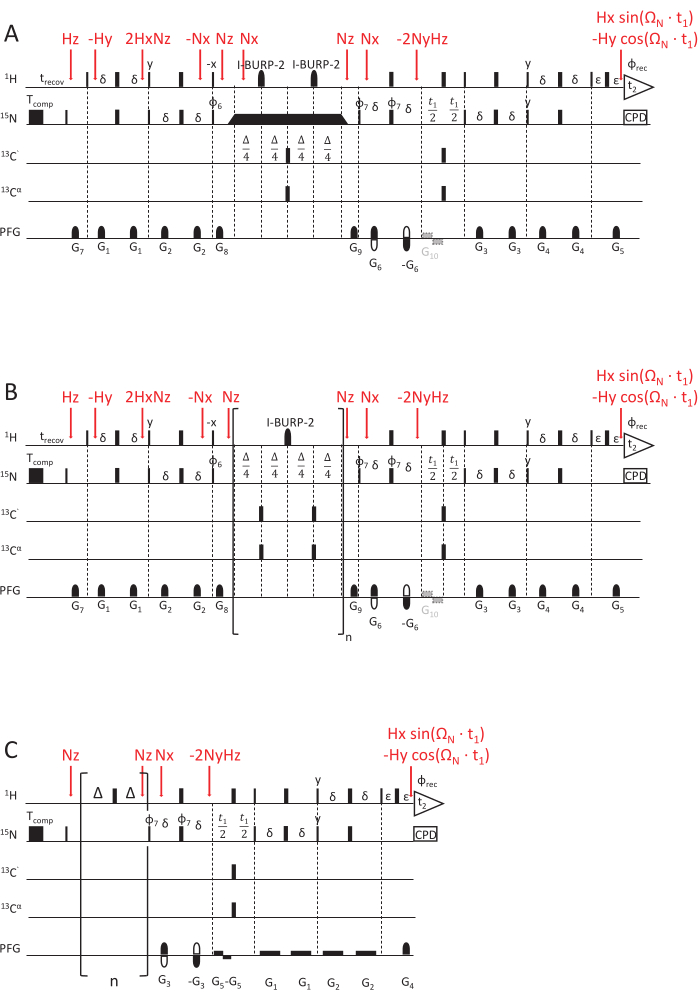
Abbildung 2: NMR-Pulssequenzschemata zur Bestimmung der NMR-Relaxationsratenkonstanten. (A) 15N R1ρ, (B) 15N R1 und (C) hetNOE-Experiment unter Verwendung eines empfindlichkeitsverstärkten HSQC-Ausleseschemas69,70. 90°(x)-Impulse werden durch schmale Rechtecke und 180°(x)-Impulse durch breite Rechtecke visualisiert, sofern nicht anders angegeben. Der folgende Phasenzyklus wird angewendet: φ6 = y, y, -y, -y; φ7 = y, -y, φrec = y, -y, -y, y. Die Quadraturdetektion wird durch Umkehrung der Polarität des Gradienten G5 und des Phasenzyklus von φ7 (Echo/Anti-Echo-Detektion) erreicht. (A) 15N R1ρ Experiment: Das schwarze Rechteck stellt den Spin-Lock dar, für den die Dauer variiert, um unterschiedliche Relaxationsverzögerungen zu erhalten. Die Dreiecke vor und nach dem Spin-Lock zeigen die adiabatischen Formpulse an, die die Magnetisierung entlang der effektiven Magnetfeldachse Beff ausrichten. G10 ist ein optionaler Gradient, um eine Strahlungsdämpfung der Wassermagnetisierung während der Entwicklungsphase zu verhindern. (B) 15N R1 Experiment: Der in Klammern gesetzte Teil zeigt das Schleifenelement der Sequenz, das n Mal wiederholt wird, um der gewünschten Relaxationsverzögerung zu entsprechen. (C) Das hetNOE-Pulsschema ähnelt der zweiten Hälfte der R1- und R1ρ-Pulsschemata, nämlich der t1-Entwicklungszeit und dem HSQC-Detektionselement. Die 15N-Magnetisierung wird jedoch direkt angeregt, ohne dass INEPT vorhanden ist. Die Sättigung der Protonenmagnetisierung (um eine Kreuzrelaxation zwischen 1H und 15N zu erreichen) wird durch einen Zug von 180(1H) Pulsen erreicht, der mindestens 5 s lang angelegt wird. Für das Referenzexperiment wird eine Leerlaufverzögerung von gleicher Länge (hier 5 s) ohne Pulsfolge verwendet. G5 ist ein optionaler Gradient zur Verhinderung von Strahlungsdämpfung, und die Inversion der Polarität des Gradienten G4 in Kombination mit der Phase φ7 = y, -y, -y, y erreicht eine Quadraturdetektion. Die Magnetisierungstransferschritte, dargestellt durch Produktoperatoren, sind rot markiert. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Die Relaxationsgeschwindigkeitskonstante R2 beschreibt die Relaxation der transversalen Polarisation (in der xy-Ebene orthogonal zum externen Magnetfeld) aufgrund des Verlusts der Phasenkohärenz zwischen dem Spin, was zu einem Abfall der nachweisbaren Magnetisierungführt 53,54. Die spektrale Dichtefunktion bei hohen und kleinen Frequenzen trägt ähnlich wie R1 zu R2 bei. Der größte Beitrag zu R2 ergibt sich jedoch aus der spektralen Dichte bei Nullfrequenz. Aus diesem Grund reagiert R2 sehr empfindlich auf das Rotationstaumeln, das durch die Rotationskorrelationszeit τ R beschrieben wird, die für ein kleines globuläres Protein bei Raumtemperatur in der Größenordnung von wenigen ns liegt. Daher tragen langsamere Rückgratbewegungen im Bereich von Hunderten von ps bis niedrigem ns-Bereich am meisten bei. Die Austauschdynamik des Rückgrats, die eine Modulation des isotropen Teils des chemischen Verschiebungstensors der 15N-Kerne bewirkt, addiert im Prinzip einen Austauschbeitrag R2ex zu den R 2-Geschwindigkeitskonstanten 43,44,49,60,61. In den beschriebenen Experimenten wird der R2ex-Beitrag durch einen Spin-Lock unterdrückt, der die Dynamik langsamer als die inverse Zirkularfrequenz des Spin-Lock neu fokussiert. Der Spin-Lock ist ein langer Dauerstrich-Hochfrequenzimpuls, der die Magnetisierung entlang der effektiven Magnetfeldachse Beff ausgerichtet hält (die Vektorsumme des Spin-Lock-Feldes ω1 und des chemischen Verschiebungsversatzes von der 15N Trägerfrequenz (siehe unten)). Die Relaxation der Magnetisierung, die entlang der B1,eff-Achse ausgerichtet ist, wird alsR1ρ-Relaxation bezeichnet, die eineR1-Komponente und eineR2-Komponente aufweist. Mit der Formel (1) kann R2 aus R1ρ und R144,73 berechnet werden:

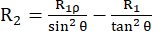figure-introduction-20016 (1).

Der Winkel zwischen der Achse des effektiven Magnetfeldes Beff und dem externen Magnetfeld B0 ist 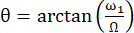figure-introduction-20258. ω1 ist die HF-Amplitude der Spinsperre und Ω der chemische Verschiebungsversatz zwischen der chemischen Verschiebung des entsprechenden Rests um 15N und der Trägerfrequenz 44,73 von 15 N.

Das R1ρ-Impulsschema (Abbildung 2A, 70) ist dem 15N R1-Schema sehr ähnlich, mit Ausnahme der Relaxationsverzögerung. Um die Relaxationsraten von 15N R1ρ zu messen, muss der Spin-Lock aktiv sein, nachdem die Magnetisierung entlang der effektiven Feldachse Beff durch einen adiabatischen Impuls mit der gleichen Hochfrequenz-Amplitude (RF) wie der Spin-Lock ausgerichtet wurde. Die Länge des Spin-Locks wird variiert, um die verschiedenen Relaxationsverzögerungen zu erhalten.

Der stationäre {1H}-15N nukleare Overhauser-Effekt (1 H-15N NOE), im Folgenden als hetNOE bezeichnet, ist das Verhältnis der Kreuzrelaxationsrate und der longitudinalen Relaxationsrate von 15N. Sie führt zu einer Verringerung der stationären Polarisation auf 15N aufgrund der Kreuzrelaxation mit dem Proton bei Sättigung der Protonenpolarisation 45,53,54,74,75. Die Kreuzrelaxation hängt von den spektralen Dichtefunktionen der Summe und Differenz der 1H und 15N Larmor-Frequenzen ab. Daher ist der hetNOE sowohl für die schnelle Pikosekundendynamik (< 100 ps) als auch für die ps-ns-Dynamik (aufgrund seiner R1-Abhängigkeit) empfindlich. Die Sequenz69 (Abbildung 2C) basiert auf einer empfindlichkeitsverstärkten HSQC-Auslesung mit Echo/Anti-Echo-Gradienten für die Quadraturdetektion. Für die Sättigung der Protonenmagnetisierung und die resultierende hetNOE wird die Gleichgewichtsprotonenmagnetisierung invertiert und anschließend durch schnell pulsierende 180°-Pulse um etwa das 5-fache der 15 N T1 gesättigt. Für das Referenzexperiment ist die Erholungsverzögerung gleich der Sättigungsverzögerung, jedoch ohne die Impulsfolge von 1H 180°. Eine zusätzliche Verzögerung von D1 = 2 s wird für das Referenzexperiment und das Experiment mit 1H Sättigung hinzugefügt. Beide Experimente werden hintereinander aufgezeichnet und unterscheiden sich nur in der Anwendung von 1H 180°-Pulsen (Sättigung) oder nicht (Referenz). Das Verhältnis der im Experiment mit 1H Sättigung aufgezeichneten spektralen Intensitäten dividiert durch die Intensitäten des Referenzexperiments (ohne die 180°-Protonenpulsfolge) ergibt den Wert {1H}-15N NOE (hetNOE).

Das folgende Protokoll beschreibt den Aufbau von NMR-Relaxationsexperimenten von Lakomek et al.69 und Stief et al.70. Wir konzentrieren uns auf NMR-Pulssequenzen unter Verwendung eines empfindlichkeitsverstärkten HSQC-Detektionsschemas. Die 15N R1 und R1ρ Experimente werden wie von Stief et al.70 ausführlich beschrieben durchgeführt, und das hetNOE-Experiment wird von Lakomek et al.69 beschrieben.

Protokoll

1. Vorbereitung der NMR-Probe

HINWEIS: Die Isotopenmarkierung der Proteine wird für höherdimensionale NMR- und fortgeschrittene NMR-Experimente durchgeführt. Wenn die Proteinexpression in E. coli und die Proteinreinigung unter Verwendung von Rich Media (z. B. Luria-Bertani [LB] oder 2x Hefeextrakt Tryptonmedium [2YT]) mit einer Ausbeute von mehreren Milligramm pro Liter etabliert wurden, ist die Herstellung einer isotopenmarkierten NMR-Probe in der Regel relativ einfach.

  1. Verwenden Sie für die Isotopenmarkierung M9-Minimalmedien für die Genexpression, wobei 15N Ammoniumchlorid die einzige Stickstoffquelle und 13C angereicherte Glukose die einzige Kohlenstoffquelle ist.
  2. Für die Proteinaufreinigung ist das im Labor etablierte Standardprotokoll für das jeweilige Protein zu befolgen.
    HINWEIS: Der Abschnitt "Ergebnisse" zeigt repräsentative Ergebnisse für ein IDP, das monomere SNARE-Protein Synaptobrevin-2 (1-96). Die NMR-Isotopenmarkierung von Synaptobrevin-2 wurde wie in70 beschrieben durchgeführt. Für sehr hochpräzise Messungen wird die Verwendung niedriger D2O-Konzentrationen von weniger als 5 % empfohlen. Dies ist auf den Deuterium-Isotopeneffekt zurückzuführen, der in Hahn-Echo 15N T2 und bei niederfrequenten 15N CPMG-Relaxationsdispersionsexperimenten (hier nicht diskutiert) beobachtet werden kann, aber in 15N R1ρ-Experimenten (wo er hauptsächlich refokussiert wird) nur einen minimalen Einfluss hat76.

2. Vorbereitungen für die Durchführung der NMR-Relaxationsexperimente am Spektrometer

HINWEIS: Die beschriebenen NMR-Relaxationsexperimente sind spezifisch für Bruker-Spektrometer. Sie wurden auf kryogenen Dreifachresonanzsonden mit 1H, 15N und 13C bei Raumtemperatur sowie auf Avance III- und Avance Neo-Konsolen getestet, die mit der Bruker-Software Topsin 3.6 oder höher betrieben wurden.

  1. Befolgen Sie die Vorsichtsmaßnahmen.
    1. Führen Sie eine Sicherheitseinweisung durch, bevor Sie am NMR-Spektrometer arbeiten.
    2. Überprüfen Sie die Leistungsangaben der Sonde des verwendeten Spektrometers und wählen Sie für jeden Puls eine geeignete Pulslänge und Pulsleistung, z.B. durch einen Vergleich der Konsistenz mit den Topspin "prosol"-Tabelleneinträgen.
  2. Importieren Sie die Impulssequenzen.
    1. Laden Sie die NMR-Pulsprogramme entweder von der unten angegebenen Website oder aus dem erweiterten Biological Magnetic Resonance Bank (BMRB) Repository (bmrbig102) in das Verzeichnis /opt/topspin4.1.4/exp/stan/nmr/lists/pp/user des Computers herunter, der das NMR-Spektrometer betreibt. Bitte passen Sie die topspin-Version (hier: topspin4.1.4 auf die jeweils auf dem Spektrometer installierte Version) an.
    2. Laden Sie die NMR-förmigen Pulse entweder von der unten angegebenen Website oder aus dem erweiterten Repository der Biological Magnetic Resonance Bank (BMRB) (bmrbig102) in das Verzeichnis /opt/topspin4.1.4/exp/stan/nmr/lists/pp/user des Computers herunter, der das NMR-Spektrometer betreibt. Bitte passen Sie die topspin-Version (hier: topspin 4.1.4 auf die jeweils auf dem Spektrometer installierte Version) an.
  3. Kalibrieren Sie das Spektrometer und die Probe.
    1. Stellen Sie die gewünschte Temperatur ein. Wenden Sie für die Temperaturkalibrierung die Protokolle der Einrichtung an. Verwenden Sie beispielsweise eine Methanol-d4-Probe und interpretieren Sie die beobachtete chemische Verschiebungsdifferenz mit dem NMR-Thermometer (https://chem.ch.huji.ac.il/nmr/software/thermometer.html) der Webanwendung. Siehe auch77.
    2. Die Probe (zuzüglich zusätzlicher 5 % D2O für die Verriegelung) einführen und ca. 10 Minuten warten, damit die Probe ihre Temperatur ausgleichen kann. Sperren Sie das Deuteriumsignal (2H) (Befehl: sperren, H2O+D2O wählen).
    3. Passen Sie die Kanäle 1H, 15N und 13C an und stimmen Sie sie ab, z. B. mit der atma- oder atmm-Routine.Wenn keine automatische Abgleich- und Abstimmeinheit installiert ist, passen Sie die Sonde manuell mit dem Wobb-Befehl an und stimmen Sie sie ab.
    4. Führen Sie Shimming für ein homogenes B0-Feld durch, z. B. mit der Topshim-Routine tg.
  4. Kalibrieren Sie die Impulslänge von 90° (1H).
    1. Verwenden Sie das zg-Experiment. Verwenden Sie getprosol , um die Sondenparameter zu importieren. Wählen Sie eine kurze Dauer von 5 μs für P1. Überprüfen und korrigieren Sie bei Bedarf den angegebenen Leistungspegel der Sonde für PLW1.
    2. Starten Sie das Experiment mit zg. Verarbeiten Sie die Daten mit efp. Passen Sie die Phase mit an.pH-Wert , so dass die Basislinie gleichmäßig ist und das NMR-Signal der Wasserresonanz in Phase ist.
    3. Schätzen Sie einen 360° (1H) Puls, indem Sie einen üblichen oder ungefähren 90° (1H) Impuls (z. B. aus den aufgeführten Spektrometerspezifikationen) nehmen und mit dem Faktor vier multiplizieren. Führen Sie das Experiment aus, und verarbeiten Sie es.
      HINWEIS: Die gewählte Dauer ist zu lang, wenn das Signal positiv ist, und zu kurz, wenn es negativ ist. Der 360° (1H) Impuls ist der Nulldurchgang.
    4. Passen Sie die Impulslänge entsprechend an. Führen Sie dies iterativ aus, um den Nulldurchgang zu finden. Teilen Sie den erhaltenen Wert durch vier. Das wird der 90° (1H) Puls sein.
      HINWEIS: Eine Alternative zur beschriebenen 360°-Methode ist die Pulsroutine , die von der Kommandozeile aus gestartet werden kann und eine automatisierte 1H Impulskalibrierung ermöglicht.
  5. Kalibrieren Sie die Trägerfrequenz O1 auf die Wasserresonanz.
    1. Kopieren Sie das zg-Experiment, indem Sie edc in die Befehlszeile eingeben, in eine neue Experimentnummer. Geben Sie rpar ein, um die Parametersätze zu öffnen (Ergänzende Abbildung 1A).
    2. Suchen Sie nach dem Parametersatz ZGPR. Klicken Sie auf den Parametersatz ZGPR (Ergänzende Abbildung 1A), klicken Sie auf Lesen, wählen Sie "getprosol" ausführen und klicken Sie auf OK (Ergänzende Abbildung 1B).
    3. Ändern Sie P1 auf die kalibrierte Impulslänge von 90° (1H). Wählen Sie eine Sättigungslänge von D1 = 2 s und eine Impulsleistung von PLW9 von 50 dB. Stellen Sie die Empfängerverstärkung (rg) auf 16 ein. Alternativ können Sie die Einstellung der Empfängerverstärkung ausführen, indem Sie rga eingeben und die Empfängerverstärkung auf den angegebenen Wert einstellen (aber vermeiden Sie "Empfängerverstärkungsüberlauf").
    4. Geben Sie gs in die Befehlszeile ein, um eine wiederholte, kontinuierliche Erfassung zu starten. Gehen Sie zum Erfassungsfenster und ändern Sie den O1-Faktor, um den FID-Bereich zu reduzieren, der vom Wassersignal dominiert wird (Ergänzende Abbildung 2).
    5. Klicken Sie unter die Markierung, um den O1-Wert zu verringern, und klicken Sie über die Markierung, um ihn zu erhöhen. Verwenden Sie die Empfindlichkeitstaste, um die Schrittgröße zu ändern. Speichern Sie das aktuelle O1; Close stoppt die wiederholte Erfassung (Ergänzende Abbildung 2).
  6. Kalibrieren Sie die Impulslänge von 90° (15N).
    1. Kopieren Sie das zg-Experiment in eine neue Versuchsnummer (Typ edc). Geben Sie rpar ein, um den Parametersatz zu lesen HSQCFPF3GPPHWG das Impulsprogramm auf ein 1H-15 N HSQC-Experiment zu ändern. Verwenden Sie die Option Parameter P1, O1 und PLW1 beibehalten (Ergänzende Abbildung 1).
    2. Geben Sie getprosol 1H 1H) Impulslänge in μs> <90° (1H) Impulsstärke in db> in die Befehlszeile ein, um die Sondenparameter zu importieren. Legen Sie die Anzahl der Scans (NS) auf 8 und die Anzahl der Dummy-Scans (DS) auf 2 fest.
      HINWEIS: < > gibt hier die Werte an, die eingestellt werden sollen. Zum Beispiel: getprosol 1H 8.5 -11.79.
    3. Führen Sie das erste Inkrement des Experiments aus, indem Sie zg in die Befehlszeile eingeben. Kopieren Sie das erste Inkrement in eine neue Versuchsnummer mit rser 1 . Verarbeiten Sie die Daten mit efp und phasen Sie das Spektrum mit .Tel. Verwenden Sie das erste Inkrement (1D-Experiment) des Experiments für die folgenden Schritte.
      HINWEIS: Der < > die gewählte Nummer für das neue Experiment angeben, z. B. rser 1 101.
    4. Geben Sie ased in die Befehlszeile ein, um die Impulssequenzparameter des 1D-Experiments zu öffnen. Klicken Sie auf das E in der PULPROG-Zeile (siehe Ergänzende Abbildung 3A), um den Impulsprogramm-Editor zu öffnen.
    5. Gehen Sie wie folgt vor, um die Impulssequenz unter einem neuen Namen zu speichern: Klicken Sie auf Datei (linke obere Ecke), Speichern unter, geben Sie den neuen Namen ein und klicken Sie auf OK. Klicken Sie dann auf PULPROG auf den Datensatz setzen (siehe Ergänzende Abbildung 3B) und klicken Sie auf OK.
    6. Modifizieren Sie die ursprüngliche 1 H-15N HSQC-Sequenz (unter einem neuen Namen gespeichert, siehe 2.6.4.), indem Sie die 90° (15N) nach der t 1-Entwicklungsperiode (vor der Rückübertragung) mit dem Faktor 2 multiplizieren (der 90° (15N)-Impuls ist jetzt 180° (15N)). Drücken Sie Strg S, um die Impulssequenz zu speichern. Stellen Sie die Impulslänge auf 90° (15N) (P21) ein, so dass das NMR-Signal des ersten Inkrements verschwindet (am Nulldurchgang) (Ergänzende Abbildung 3B).
    7. Öffnen Sie das 1 H-15N HSQC-Experiment (2D-Experiment) und geben Sie die kalibrierte 90° (15N) Pulslänge (P21) ein. Geben Sie getprosol 1H 1H) Pulslänge in μs> <90° (1H) Pulsstärke in db> 15N 15N) Pulslänge in μs> <90° (15N) Pulsstärke in db> in der Kommandozeile ein.
  7. Bestimmen Sie die spektralen Breiten und die Berücksichtigung der Aufnahmezeiten.
    1. Passen Sie im Erfassungsparameterfenster für das HSQC-Experiment 1 H-15N (geben Sie eda in der Befehlszeile ein) die spektrale Breite (Erfassungsparameter SW) und die Anzahl der Dimensionsinkremente in direkten und indirekten Dimensionen (Erfassungsparameter TD) an.
      1. Wählen Sie SW, 16 ppm in der direkten (1H) und 30 ppm in der indirekten (15N) Dimension. Wählen Sie TD, 2048 in der direkten (1H) und 512 in der indirekten (15N) Dimension.
    2. Erfassen Sie das 1 H-15N HSQC-Experiment.
      1. Überprüfen Sie, ob alle Signale von Interesse erkannt werden und dass keine Aliasing-Artefakte im Spektrum vorhanden sind. Ändern Sie das O3P, wenn die Mitte des Spektrums nicht mit der Mitte der Proteinsignalverteilung entlang der 15N-Achse übereinstimmt.
      2. Erhöhen Sie die SW , wenn das Spektralfenster zu klein ist. Erhöhen Sie den TD , um eine höhere FID-Auflösung zu erhalten (Überprüfen Sie die Sondenspezifikationen für die maximale Dauer der Entkopplung).
        HINWEIS: Dies ist der allgemeine Aufbau und der Ausgangspunkt für den Aufbau von NMR-Relaxationsexperimenten. Es wird empfohlen, das 1 H-15N HSQC-Experiment zu Beginn und am Ende des gesamten Versuchssatzes und bei längeren Versuchszeiten auch dazwischen aufzuzeichnen, um die Integrität der Probe zu überwachen.

3. Durchführung der NMR-Relaxationsexperimente

HINWEIS: Die NMR-Relaxationspulssequenzen (Abbildung 2) sind in https://www.ipb.hhu.de/en/teams/team-lakomek/pulsesequences oder im erweiterten Repositorium der Biologischen Magnetresonanzbank (BMRB) (bmrbig102) verfügbar.

  1. Richten Sie die 15N R1ρ Experiment.
    1. Kopieren Sie das HSQC-Experiment (Typ edc) in ein neues Verzeichnis. Geben Sie ased ein und ändern Sie das Impulsprogramm auf das Experiment 15N R1ρ , indem Sie auf die drei Punkte der Parameterzeile PULPROG in den Parametern der Impulssequenz klicken (ased, siehe Ergänzende Abbildung 3A). Doppelklicken Sie auf das Impulsprogramm, klicken Sie auf Set PULPROG to dataset (siehe Ergänzende Abbildung 3B) und klicken Sie auf OK.
      HINWEIS: Es können einige Fehlermeldungen angezeigt werden. Schließen Sie diese Meldungen.
    2. Geben Sie gpnam in die Befehlszeile ein, um alle fehlenden Gradientenformen (gpnam1 - gpnam9) einzufügen, wie in der Impulssequenz beschrieben (Ergänzende Abbildung 4).
    3. Geben Sie vplist in die Befehlszeile ein. Klicken Sie auf die drei Punkte (Ergänzende Abbildung 5A), Datei (obere linke Ecke) und Neu (Ergänzende Abbildung 5B).
    4. Geben Sie einen Namen für eine neue Dummy-vplist ein, und drücken Sie OK. Erstellen Sie die Dummy-vplist (5m, 65m, 25m, 45m, 15m, 55m, 35m, 10m; für jeden vplist-Eintrag eine neue Zeile). Drücken Sie Strg S , um die Liste zu speichern und das Fenster der vplist zu schließen (Ergänzende Abbildung 5C).
    5. Doppelklicken Sie auf den Namen der neu erstellten vplist (Ergänzende Abbildung 5B).
      HINWEIS: Dies ist notwendig, um Kompilierungsfehler in der Impulssequenz zu vermeiden. Die entsprechenden Einträge in der vplist werden weiter unten festgelegt (Ziff. 3.1.29.).
    6. Geben Sie ased ein, um die Parameter der Impulssequenz zu öffnen (Ergänzende Abbildung 6). Geben Sie alle fehlenden Gradientenstärken und Gradientenlängen ein, wie in der Impulssequenz angegeben (Ergänzende Abbildung 6D).
    7. Geben Sie für den Schleifenzähler L3 (Anzahl der komplexen Punkte in der indirekten Dimension) 1/2 des Eintrags 15N TD im Erfassungsparameterfenster (eda) ein. Geben Sie für den Schleifenzähler L6 die Anzahl der aufgezeichneten Relaxationsdatenpunkte ein, die für die Anpassung der Relaxationskurve verwendet wurden.
      HINWEIS: Diese Nummer L6 entspricht der Anzahl der vplist-Einträge, hier: 8 (Ergänzende Abbildung 6A).
    8. Legen Sie den adiabatischen TanhTan_half.nl-Impuls, der von der oben angegebenen Website heruntergeladen wurde, als Form des 15N SP8-Impulses fest. Stellen Sie den adiabatischen TanhTan_2nd.nl-Impuls von der Website als Form des 15N SP9-Impulses ein (Ergänzende Abbildung 6C).
    9. Stellen Sie den P8-Eingang auf die Länge des adiabatischen TanhTan-Impulses ein - lang genug, um die Adiabatizität des Impulses zu gewährleisten; hier wird P8 = 3000 μs gewählt (Ergänzende Abbildung 6C).
    10. Legen Sie die 15-N-Entkopplung (CPDPRG 3) auf ein garp-Entkopplungsschema fest. Für die Länge der Entkopplung PCPD3 200 μs verwenden (Ergänzende Abbildung 6C).
    11. Legen Sie die Interscan-Wiederherstellungsverzögerung auf mindestens D1 = 2 s oder länger fest.
      HINWEIS: Informationen zur Auswahl einer angemessenen Wiederherstellungsverzögerung finden Sie im Abschnitt Diskussion.
    12. Setzen Sie die Dummy-Scans (DS) für das abschließende Experiment auf mindestens 64 (beim Aufbau ist DS = 4 aus Zeitgründen ausreichend). Verwenden Sie als Ausgangspunkt eine Anzahl von Scans (NS) von 4. Verwenden Sie ein Vielfaches von 4, wenn das Signal-Rausch-Verhältnis (SNR) zu niedrig ist (Ergänzende Abbildung 6A).
    13. Stellen Sie den O1 auf die kalibrierte Trägerfrequenz aus Schritt 2.5 ein. Stellen Sie den O2P auf 176 ppm ein und kopieren Sie den O3P aus dem 1 H-15N HSQC-Experiment (Ergänzende Abbildung 6A-C).
    14. Stellen Sie die Impulslänge P7 auf die in Schritt 2.6 kalibrierte Impulslänge von 90° (15N) ein. Kopieren Sie außerdem den Impulsleistungspegel des 90° (15N) Impulses aus Schritt 2.6 in PLW3 und PLW7 (Ergänzende Abbildung 6C).
    15. Stellen Sie die Impulslänge P1 und P19 auf die in Schritt 2.4 berechnete Impulslänge von 90° (1H) ein. (Ergänzende Abbildung 6B).
    16. Legen Sie die Anzahl der Inkremente in der indirekten Dimension TD =l 3 * 2 * l6 fest (eda oder geben Sie td in der Befehlszeile ein).
      HINWEIS: Alle hier beschriebenen Parameter der Impulsfolge sind zusätzlich in der Impulsfolge annotiert.
    17. Stellen Sie den Formimpuls SP5 auf eine I-BURP2-Form (Iburp2.1000) ein. Stellen Sie die Pulslänge P15 auf 2000 μs ein. Öffnen Sie die Anzeige des Formwerkzeugs, indem Sie auf das E neben dem I-BURP2-Formimpuls im Parameterfenster der Topspin-Impulssequenz (ased) klicken (Ergänzende Abbildung 6B).
    18. Simulieren Sie den Formimpuls mit der richtigen Länge, indem Sie auf die Schaltfläche NMR-Simulation starten klicken. Überprüfen Sie im Simulationsfenster die geformte Pulslänge [μs] (= 2000 μs) und den Drehwinkel [°] (= 180°). Klicken Sie auf NMR-SIM starten (ergänzende Abbildung 7A).
    19. Überprüfen Sie den Anregungsbereich und wählen Sie die geeignete I-BURP2-Pulslänge, um die spektrale Dispersion des Proteins von 1H abzudecken und gleichzeitig eine Anregung des Wassers zu vermeiden. Stellen Sie P15 auf die Länge des geformten Pulses des Simulationsfensters ein, in dem der beste simulierte IBURP-2-Impuls simuliert wird (Ergänzende Abbildung 7B).
      HINWEIS: Die richtige Länge wird gewählt, wenn der I-BURP2 die gesamte Amidregion anregt (> 95% Wirksamkeit). Um einen I-BURP2-Impuls mit einer anderen Länge zu simulieren, schließen Sie das Fenster mit dem Anregungsprofil und bearbeiten Sie die Länge des geformten Pulses im Simulationsfenster. Klicken Sie auf NMR-SIM starten. Pulse mit kürzerer Länge haben einen breiteren Anregungsbereich in Hz.
    20. Stellen Sie SPOFFS5 ein, um die Trägerfrequenz des I-BURP2-Impulses zu ändern, und verschieben Sie den Anregungsbereich nach links oder rechts, um zu vermeiden, dass der I-BURP2-Impuls die Wassermagnetisierung berührt und stört (Ergänzende Abbildung 6B).
    21. Um die geeignete Leistungsstufe des geformten Pulses zu bestimmen, öffnen Sie das Bruker-Formwerkzeug, klicken Sie auf die Schaltfläche NMR-Simulation starten und stellen Sie die Länge des I-BURP2-Pulses auf Geformte Pulslänge [μs] ein. Merken Sie sich die entsprechende Länge eines weichen rechteckigen 90° (1H) Impulses, der im Simulationsfenster bei dem entsprechenden 90° Rechteckimpuls [μs] sichtbar ist (Ergänzende Abbildung 7A).
    22. Geben Sie calcpowlev ein. Als Referenzlänge wird der harte 90° (1H)-Impuls (P1) in Mikrosekunden (Ergänzende Abbildung 8B) und als neue Länge der weiche Rechteckimpuls 90° (1H) entsprechend dem I-BURP2-Impuls in Mikrosekunden (Ergänzende Abbildung 8A) verwendet. Merken Sie sich die Leistungsdifferenz Δ in dB zwischen dem harten 90° (1H) Impuls und dem weichen rechteckigen Impuls (Ergänzende Abbildung 8C). Kopieren Sie die Impulsstärke des harten 90° (1H) Impulses in dB nach SPW5 und addieren Sie die gespeicherte Differenz Δ in dB (Ergänzende Abbildung 6B).
    23. Um die Leistungspegel des Spin-Locks zu bestimmen, berechnen Sie die entsprechende Impulslänge des Spin-Lock von 90° (15N). Verwenden Sie die Formel: 90° (15N) Impulslänge in s = 0,25 / (Spin-Lock-Leistung in Hz).
    24. Mit dem Calcpowlev wird die Leistungsdifferenz Δ in dB zwischen der Leistung des Spin-Lock und dem 90° (15N) harten Impuls (P7) berechnet. Neu: 90° (15N) Pulslänge des Spin-Lock in μs (Ergänzende Abbildung 8A). Ref: harte 90° (15N) Pulslänge in μs (Ergänzende Abbildung 8B). Kopieren Sie den Leistungspegel PLW7 des 90° (15N) harten Impulses in dB auf den Spin-Lock-Leistungspegel PLW8 (Ergänzende Abbildung 6C) und addieren Sie die berechnete Leistungsdifferenz Δ in dB (Ergänzende Abbildung 8C).
    25. Kopieren Sie den Leistungspegel des Spin-Lock-PLW8 in die Leistungsstufen SPW8 und SPW9. (Ergänzende Abbildung 6C).
    26. Um die Leistungspegel der 15-N-Entkopplung zu bestimmen, wird mit dem Calcpowlev die Leistungsdifferenz Δ zwischen der Leistung des 90° (15N) Entkopplungsimpulses (PCPD3) und dem 90° (15N) harten Impuls (P7) berechnet. Neu: PCPD3 in μs (200) (Ergänzende Abbildung 8A). Ref: harte 90° (15N) Pulslänge in μs (Ergänzende Abbildung 8B). Kopieren Sie den Leistungspegel PLW7 des 90° (15N) harten Impulses in dB auf den Entkopplungspegel PLW31 (Ergänzende Abbildung 6C) und addieren Sie Δ in dB (Ergänzende Abbildung 8C).
    27. Um die Temperaturkompensation zu verwenden, fügen Sie #define TEMP_COMPENSATION ein (indem Sie das Semikolon in der Impulssequenz löschen). Stellen Sie P18 auf die maximale Dauer der Spin-Lock-Sperre ein, die im 15N R1ρ-Experiment verwendet wurde.
      HINWEIS: Es wird empfohlen, die Temperaturkompensation für den ersten Versuch des Versuchs auszuschalten.
    28. Bei 15N 13C beschrifteten Proben fügen Sie # ein, um LABEL_CN im Impulsprogramm zu definieren (durch Löschen des Semikolons in der Impulssequenz). Stellen Sie P4 auf die Impulslänge ein, die mit der Formel in78 berechnet wurde. Er entspricht z.B. 23,70 μs bei 600 MHz und 11,85 μs bei 1200 MHz. Geben Sie calcpowlev ein, um die Leistungsdifferenz in dB zwischen P4 und dem (13C) harten Impuls zu berechnen. Kopieren Sie die harte Impulsleistung (13C) in dB nach PLW4 und addieren Sie das Δ in dB. Kopieren Sie PLW4 nach PLW2 (ergänzende Abbildung 6B).
    29. Bestimmen Sie die Relaxationsverzögerungen für eine geeignete Probenahme.
      1. Führen Sie die ersten acht FIDs (im Fall L6 = 8) durch und verarbeiten Sie diese (rser < neue Versuchsnummer>). Wählen Sie die Einträge in der vplist, dass die Spitzenintensität des Experiments mit der längsten Verzögerung auf mindestens 1/e (ca. 37%), aber nicht weniger als 25% im Vergleich zum Experiment mit der kürzesten Verzögerung (die als Referenz dient) abnimmt.
      2. Passen Sie die verbleibenden Einträge der vplist an, um eine gleichmäßige Abtastung der Intensitätsabnahmen zwischen dem FID mit der längsten Verzögerung und dem FID mit der kürzesten Verzögerung zu erreichen. Lesen Sie den HINWEIS und die Leistungsspezifikationen der Sonde.
        HINWEIS: Die langsam entspannenden Rückstände dominieren den ersten FID. Passen Sie die verbleibenden Einträge der vplist an, um eine gleichmäßige Abtastung der Intensitätsabnahmen zwischen dem ersten und zweiten FID zu erreichen. Überschreiten Sie nicht die maximal zulässige Spin-Lock-Leistung und -Länge der Sonde (konsultieren Sie das Sondenhandbuch und die Sondenspezifikationen). Im Falle einer Temperaturkompensation ist P18 (maximale Spin-Lock-Dauer) zu überprüfen, da die Gesamtdauer der Spin-Lock-Funktion von P18 angewendet wird, aufgeteilt zwischen der Relaxationsverzögerung und der Temperaturkompensation. Es hält Zeit (Relaxationsverzögerung) + Zeit (Temperaturkompensation) = const = P18. Bei einem Spin-Lock von 2 kHz bevorzugen wir es, eine Spin-Lock-Dauer von mehr als 65 ms nicht zu überschreiten, wobei eine Wiederherstellungsverzögerung (D1) von 2 s verwendet wird. In diesem Fall muss ein Kompromiss zwischen der maximalen Spin-Lock-Dauer und der längsten Relaxationsverzögerung zugunsten der maximal zulässigen Spin-Lock-Dauer eingegangen werden. Bei längeren D1-Wiederherstellungsverzögerungen können längere Spin-Lock-Leistungen anwendbar sein. Was zählt, ist die Gesamtleistungsdeposition in der Sonde im Laufe der Zeit. Wenn längere Spin-Lock-Dauern erforderlich sind, erhöhen Sie die Spin-Lock-Längen nur in kleinen Schritten und beobachten Sie das Lock-Signal. Als Faustregel gilt, dass Sie die Sperrstufe im oberen Drittel Ihres Schlossdisplays anpassen sollten. Wenn sich der Sperrpegel während der Ausführung der Impulssequenz um mehr als zwei Quadrate verringert, ist die in der Sonde abgelagerte Spin-Lock-Leistung zu hoch.
    30. Geben Sie rga in die Befehlszeile ein, um die Empfängerverstärkung zu bestimmen. Für ein gutes Signal-Rausch-Verhältnis streben Sie einen Empfängerverstärkungswert (rg) zwischen 128 und 256 an, was eine gute Wasserunterdrückung beweist.
      HINWEIS: Eine Empfängerverstärkung zwischen 128 und 256 kann nicht erreicht werden, deutet auf ein zu starkes Wassersignal hin. In diesem Fall werden die Gradientenleistung und die Dauer sanft angepasst, bis die Empfängerverstärkung erreicht ist. Siehe auch den Abschnitt Diskussion.
    31. Starten Sie einen Testlauf des 15N R1ρ Experiments, indem Sie zg in die Befehlszeile eingeben. Prüfen Sie, ob das Wassersignal bei allen Verzögerungen (1 bis 8, bei 8 Verzögerungen in der vplist) gut unterdrückt wird. Überprüfen Sie auch Inkrement 9, das zweite Inkrement des Quadraturerkennungsschemas (Echo/Anti-Echo).
  2. Richten Sie das 15N R1 Experiment ein.
    1. Kopieren Sie das 15N R1ρ Experiment und ändern Sie das Impulsprogramm in das 15N R1 Experiment.
    2. Geben Sie vclist ein, generieren Sie eine vclist und geben Sie die in70 beschriebene Dummy-vclist ein: 0, 24, 6, 20, 4, 16, 8, 12; Eine neue Zeile für jeden VCLIST-Eintrag).
    3. Geöffnet alsed. Überprüfen Sie die Gradientenlängen und -stärken. Ändern Sie GPZ9 auf 14%.
    4. Überprüfen Sie die Pulslängen, Pulsformen und Pulsstärken (die korrekten Werte sollten aus dem 15N R1ρ-Experiment kopiert worden sein).
    5. Bei 15N13C markierten Proben ist #define LABEL_CN im Impulsprogramm zu verwenden.
    6. Für die Verwendung der Temperaturkompensation sind #define TEMP_COMPENSATION einzuschließen.
    7. Führen Sie die ersten acht FIDs (im Fall L6 = 8) durch und verarbeiten Sie diese (rser < neue Versuchsnummer>). Wählen Sie die Einträge in der vclist, dass die Spitzenintensität des Experiments mit der längsten Verzögerung auf mindestens 1/e (ca. 37%), aber nicht weniger als 25% im Vergleich zum Experiment mit der kürzesten Verzögerung abnimmt. Passen Sie die verbleibenden Einträge der vplist an, um eine gleichmäßige Abtastung der Intensitätsabnahmen zwischen dem FID mit der längsten Verzögerung und dem FID mit der kürzesten Verzögerung zu erreichen.
      HINWEIS: Für vclist-Einträge sind nur gerade Zahlen erlaubt.
  3. Richten Sie das Experiment {1H}-15N NOE ein.
    1. Kopieren Sie das 15N R1 Relaxationsexperiment, und ändern Sie die Impulssequenz in das Pulsschema {1H}-15N NOE.
    2. Stellen Sie die Länge der Sättigungsperiode mit dem Schleifenzähler L8 ein. Der Abstand zwischen 180° (1H) Impulsen beträgt 22 ms79 (2* 1 / JNH). Um die genauesten Ergebnisse zu erzielen, verwenden Sie eine Sättigungsperiode von etwa dem 5-fachen der 15N T1(15N) des Proteins. Hier: 5 s. Das entspräche L8 = 230.
      HINWEIS: Im Abschnitt "Diskussion" finden Sie zusätzliche Ratschläge zur Auswahl der Sättigungsperiode/Wiederherstellungsverzögerung.
    3. Ändern Sie die Länge und Stärke der Gradienten, wie im Impulsschema beschrieben. Verwenden Sie sine.20-Verlaufsformen.
    4. Legen Sie die Anzahl der Inkremente in der indirekten Dimension auf TD = l3 * 2 * 2 fest.
    5. Bei Proben, die mit 15N13C markiert sind, ist #define LABEL_CN und -DLABEL_CN als ZGOPTNS zu verwenden.
    6. Führen Sie die Impulsschemata aus, indem Sie zg in die Befehlszeile eingeben.

4. Aufbereitung und Analyse der aufgezeichneten NMR-Experimente

HINWEIS: Die Spektren wurden mit einem Bruker-System aufgenommen. Die Verarbeitung erfolgt unter Verwendung eines Unix- oder Linux-Betriebssystems. Die Spektrenverarbeitung und Datenanalyse wurde mit NMRPipe80 und python3 durchgeführt. Die NMRPipe-Software kann unter https://www.ibbr.umd.edu/nmrpipe/index.html heruntergeladen werden. NMRPipe-basierte Verarbeitungsskripte können von der Website heruntergeladen werden: https://www.ipb.hhu.de/en/teams/team-lakomek/pulsesequences oder aus dem erweiterten Repository der Biological Magnetic Resonance Bank (BMRB) (bmrbig102). Es wird empfohlen, NMRPipe zu verwenden. Wenn NMRPipe nicht verfügbar oder gewünscht ist, können Alternativen wie CCPN81 oder SPARKY (SPARKY 3 oder seine Nachfolger NMRFAM-SPARKY82 oder POKY83 ) verwendet werden.

  1. Verarbeiten und analysieren 15N R1 Experiment.
    HINWEIS: Die folgenden Befehle werden in einem Unix-Terminal ausgeführt.
    1. Kopieren Sie die Dateien im heruntergeladenen Verzeichnis R1_processing in das Verzeichnis, das die experimentellen R1-Daten enthält (Arbeitsverzeichnis).
    2. Machen Sie die Dateien mit dem Terminalbefehl ausführbar: > chmod u+x *.com
    3. Führen Sie > bruker aus, um das NMRPipe Conversion Utility zu öffnen und die fid.com Datei zu generieren. Klicken Sie auf Parameter lesen. Ändern Sie die Dimensionsanzahl in zwei, wenn drei Dimensionen gezählt werden, und klicken Sie erneut auf Parameter lesen . Klicken Sie dann auf "Skript löschen", "Skript aktualisieren" und " Skript speichern " (Ergänzende Abbildung 9).
      HINWEIS: Wenn die Trägerfrequenz nicht korrekt ist, ändern Sie das PPM für die Mittelposition, nachdem Sie zum zweiten Mal auf Parameter lesen geklickt haben.
    4. Ausführen > ./fid.com
    5. Konvertieren Sie die vclist in eine vplist mit ms Einträgen: Verzögerung in ms = 40 ms * Eintrag der vclist. Verwenden Sie > cp vclist vplist und bearbeiten Sie die vplist.
    6. Verwenden Sie > ./split.com , um die Pseudo-3D-Daten in acht 2D-Dateien aufzuteilen.
    7. Bearbeiten Sie die tauValues (vplist-Werte in der Reihenfolge der vplist) und die idxExpmt-Werte (Reihenfolge der tau-Werte in Bezug auf die Zeit) in nmrproc.com (Ergänzende Abbildung 10).
    8. Verwenden Sie > ./nmrproc.com , um die Rohdaten aller acht 2D-Spektren zu verarbeiten.
    9. Verwenden Sie > nmrDraw , um die Spektren zu zeichnen.
      1. Verwenden Sie für diese Schritte das Referenzspektrum (erster Eintrag in vplist). Wechseln Sie zu diesem Spektrum, indem Sie die Z-Dimension in eins ändern (obere linke Ecke). Passen Sie die Konturebene mit den Tasten + und - neben der Schaltfläche Faktor an. Zeichnen Sie das Spektrum mit der Schaltfläche Draw neu.
      2. Verwenden Sie einen Konturpegel, bei dem alle interessierenden Signale mit nur wenigen Signalen aus dem Rauschen erkannt werden können (der Konturpegel befindet sich am Rand des Rauschpegels) (Ergänzende Abbildung 11).
    10. Korrigieren Sie die Spektralphase, Typ v für vertikale 1D-Signalprojektion und h für horizontale 1D-Signalprojektion. Stellen Sie die Phase mit P0 und P1 ein (Ergänzende Abbildung 11), merken Sie sich die Phasendifferenz und korrigieren Sie die Phase in der nmrproc.com Datei (Ergänzende Abbildung 10).
      HINWEIS: Wenn das Spektrum in der Dimension 15N gespiegelt wird, entfernen Sie das -neg in der Zeile: | nmrPipe -fn FT -neg \ (Ergänzende Abbildung 10).
    11. Schließen Sie nmrDraw, und verarbeiten Sie den Vorgang erneut mit > nmrproc.com. Geben Sie für Peak-Picking (nachdem das Spektrum korrekt phasengesteuert wurde und das Referenzspektrum mit einer Konturebene angezeigt wird, in der alle Peaks vorhanden sind) K ein (Umschalt + k), drücken Sie Detect und klicken Sie auf Speichern. (Ergänzende Abbildung 11).
    12. Kopieren Sie eine Peakliste in das Arbeitsverzeichnis und ändern Sie -assName in ass.com in den Namen der Peakliste (Ergänzende Abbildung 12).
      HINWEIS: Ein Beispiel für eine Peakliste im richtigen Format finden Sie unter https://www.ipb.hhu.de/en/teams/team-lakomek/pulsesequences
      und im erweiterten Repositorium der Biologischen Magnetresonanzbank (BMRB) (bmrbig102).
    13. Führen Sie > ./ass.com aus, um die Spektren zuzuweisen. Überprüfen Sie die Zuweisung, die das Skript für die verschiedenen Peaks vorschlägt. Verwenden Sie die linke Maustaste zum Zuweisen und die rechte Maustaste, um Peaks zuzuweisen. Verwenden Sie die Schaltfläche Weiter , um zur folgenden Aminosäure zu gelangen, und Zurück , um zur vorherigen Aminosäure zu gelangen (Ergänzende Abbildung 13).
      HINWEIS: Die Konturebene kann mit + und - in der oberen rechten Ecke geändert werden. Mit der Schaltfläche Zeichnen können Sie das Spektrum mit der neuen Konturebene neu zeichnen (Ergänzende Abbildung 13).
    14. Nachdem Sie die Aufgabe abgeschlossen haben, klicken Sie auf Speichern und dann erneut auf Speichern . Klicken Sie anschließend auf Beenden, Abbrechen und Beenden (Ergänzende Abbildung 13).
    15. Führen Sie > python3-NoneDeleter.py aus, um relax.tab zu erstellen, die nur Informationen zu zugewiesenen Peaks enthält.
    16. Führen Sie > ./relax.com aus, um das autofit.com Skript zu generieren.
    17. Führen Sie > ./autoFit.com aus, um eine Fourier-Interpolation durchzuführen und Pseudoverhältnisse der verschiedenen Verzögerungszeiten für jede Aminosäure zu generieren (axt.tab und nlin.tab werden generiert).
    18. Führen Sie > ./model.com aus, um das modelExp.com Skript basierend auf den Daten in nlin.tab zu generieren.
    19. Führen Sie > ./modelExp.com aus, um die Evolutionskurve jedes Rests mit einem nichtlinearen Optimierungsmodell der kleinsten Quadrate anzupassen.
    20. Führen Sie > bash summary.tcl -in relax.tab > t1.tab aus. Ignorieren Sie eine mögliche Fehlermeldung: GDB Hinweis: 21 fehlende Werte in der Tabellendatei können auftreten.
    21. Kopieren Sie t1.tab in das neu erstellte Verzeichnis R1R2.
  2. Verarbeiten und analysieren Sie das 15N R1ρ Experiment.
    1. Kopieren Sie die Dateien im heruntergeladenen Verzeichnis R1rho_processing in das Verzeichnis, das die experimentellen R1ρ-Daten enthält (Arbeitsverzeichnis).
    2. Führen Sie > chmod u+x *.com
    3. Führen Sie > bruker aus, um das NMRPipe Conversion Utility zu öffnen und die fid.com Datei zu generieren. Siehe auch die Verarbeitung der 15N R1 Spektren.
    4. Ausführen > ./fid.com
    5. Führen Sie > ./split.com aus, um die Pseudo-3D-Daten in acht 2D-Dateien aufzuteilen.
    6. Führen Sie > ./nmrproc.com aus (Bearbeiten Sie vorher die tauValues [vplist-Werte] und idxExpmt ), um die Rohdaten aller acht 2D-Spektren zu verarbeiten (Ergänzende Abbildung 10).
    7. Führen Sie > nmrDraw aus, um die Spektren zu zeichnen und die Peaks auszuwählen. Verwenden Sie für diese Schritte das Referenzspektrum (erster Eintrag in vplist). Befolgen Sie das gleiche Verfahren wie beim 15N R1-Experiment .
    8. Kopieren Sie eine Peakliste in das Arbeitsverzeichnis und ändern Sie -assName in ass.com in den Namen der Peakliste (Ergänzende Abbildung 12).
    9. Führen Sie > ./ass.com aus und befolgen Sie die gleiche Vorgehensweise wie für das 15N R1-Experiment .
    10. Führen Sie > python3-NoneDeleter.py aus, um relax.tab zu erstellen, die nur Informationen zu zugewiesenen Peaks enthält.
    11. Ausführen > ./relax.com
    12. Ausführen > ./autoFit.com
    13. Ausführen > ./model.com
    14. Ausführen > ./modelExp.com
    15. Führen Sie > bash summary.tcl -in relax.tab > t1rho. tab aus. Mögliche Fehlermeldung ignorieren: GDB Hinweis: 21 fehlende Werte in der Tabellendatei können auftreten.
    16. Kopieren Sie den folgenden Header in die Datei t1rho.tab (die Werte können aus der Datei fid.com abgerufen werden) (Ergänzende Abbildung 14):
      BEMERKUNG 600MHz für T1rho
      BEMERKUNG -yOBS = 60.818 (setze hier den in fid.com gefundenen Wert)
      BEMERKUNG -yCAR = 119.06 (setze hier den in fid.com gefundenen Wert)
    17. Führen Sie > ./extract_PPM.com aus, um eine Tabelle mit dem Namen fusionOffset.tab zu erzeugen, die den Offset der Peakfrequenz von 15N relativ zur Trägerfrequenz enthält (die zur Berechnung des Winkels θ für die Extraktion von R2-Daten aus den R1 - und R1ρ-Daten benötigt wird).
  3. Fassen Sie die Relaxationsdaten zusammen.
    1. Kopieren Sie die t1rho.tab und die fusionOffset.tab in das Verzeichnis R1R2.
    2. Kopieren Sie das Skript crtR1p.tcl in das Verzeichnis R1R2, passen Sie die Spektrometerfrequenz und die Spin-Lock-Leistung an und führen Sie bash crtR1p.tcl | sort -n > R1R2.tab aus. (Ergänzende Abbildung 15). R1R2.tab enthält die angepassten R1ρ-Ratenkonstanten , den Theta-Winkel, die R2-Ratenkonstanten und die R1-Ratenkonstanten .
  4. Bearbeiten und analysieren Sie das hetNOE-Experiment.
    1. Kopieren Sie die Dateien im heruntergeladenen Verzeichnis NOE_processing in das experimentelle NOE-Datenverzeichnis (Arbeitsverzeichnis).
    2. Führen Sie > chmod u+x *.com
    3. Führen Sie > bruker aus, um das NMRPipe Conversion Utility zu öffnen und die fid.com Datei zu generieren. Klicken Sie auf Parameter lesen. Ändern Sie die Dimensionsanzahl auf zwei, wenn drei Dimensionen gezählt wurden, und drücken Sie erneut auf Parameter lesen . Drücken Sie dann auf Skript löschen, Skript aktualisieren und Skript speichern.
    4. Ausführen > ./fid.com
    5. Führen Sie > ./split.com aus (Zuvor muss eine vplist mit zwei Einträgen (0, 1) erstellt werden)
    6. Ausführen > ./ft2.com
    7. Führen Sie > nmrDraw aus, um das Spektrum zu zeichnen und die Peaks im Referenzspektrum auszuwählen (z-Dimension = 1). Extrahieren Sie das Geräusch und merken Sie es sich (drücken Sie T = Umschalt + t). Die Phasenkorrektur und das Peak-Picking folgen dem gleichen Verfahren wie beim 15N R1-Experiment .
    8. Kopieren Sie eine Peakliste in das Arbeitsverzeichnis und ändern Sie -assName in ass.com in den Namen der Peakliste (Ergänzende Abbildung 12)
    9. Führen Sie > ./ass.com aus, um die Spektren zuzuweisen. Befolgen Sie das gleiche Verfahren wie für das 15N R1-Experiment .
    10. Führen Sie > python3-NoneDeleter.py aus, um relax.tab zu erstellen.
    11. Ausführen > ./script.com
    12. Ausführen > ./autoFit.com
    13. Ändern Sie das Rauschen in error_hetnoe.tcl.
    14. Führen Sie > bash error_hetnoe.tcl |sort -n > hetNOE.tab aus

Ergebnisse

Im Folgenden werden einige beispielhafte NMR-Relaxationsdaten gezeigt, die am vesikulären SNARE-Protein Synaptobrevin-2 (1-96) aufgezeichnet wurden, das häufig als VAMP2 (vesikelassoziiertes Protein 2) bezeichnet wird. Für die Aufzeichnung der NMR-Daten verwendeten wir eine 171 μM 15N Synaptobrevin-2 (1-96) Probe (im Folgenden als Syb-2 bezeichnet) in 50 mM MES (pH 6,0) Puffer, der 150 mM NaCl, 0,1 mM TCEP und 1 mM EDTA enthielt. Alle experimentellen Daten wurden bei 278,1...

Diskussion

Dieses Protokoll beschrieb den Aufbau von NMR 15N-Relaxationsexperimenten von Lakomek et al.69 und Stief et al.70. Wir konzentrierten uns auf NMR-Pulssequenzen unter Verwendung eines empfindlichkeitsverstärkten HSQC-Detektionsschemas. Die 15N R1 und R1ρ Experimente werden wie von Stief et al.70 ausführlich beschrieben durchgeführt, und das hetNOE-Experiment wird von Lakomek et

Offenlegungen

Die Autoren erklären, dass ihnen keine konkurrierenden finanziellen Interessen oder persönlichen Beziehungen bekannt sind, die die in diesem Artikel berichtete Arbeit beeinflusst haben könnten.

Danksagungen

Wir danken Melinda Jaspert und Kevin Bochinsky für die hilfreichen Gespräche. N.L. dankt der Deutschen Forschungsgemeinschaft für die Förderung durch das Heisenberg-Programm (DFG-Förderkennzeichen 433700474). Diese Arbeit wird außerdem durch das Projekt "Virological and immunological determinants of COVID-19 pathogenesis - lessons to get prepared for future pandemics" (KA1-Co-02 "COVIPA") unterstützt, das aus dem Impuls- und Vernetzungsfonds der Helmholtz-Gemeinschaft gefördert wird. Wir danken für den großzügigen Zugang zum Jülich-Düsseldorf Biomolecular NMR Center, das gemeinsam vom Forschungszentrum Jülich und der Heinrich-Heine-Universität Düsseldorf (HHU) betrieben wird.

Materialien

NameCompanyCatalog NumberComments
Bruker 600 MHz AVANCE III HD spectrometer Brukerhttps://www.bruker.com/en/products-and-solutions/mr/nmr/avance-nmr-spectrometer.htmlNMR experiments conducted 

Referenzen

  1. Sekhar, A., Kay, L. E. An NMR view of protein dynamics in health and disease. Annu Rev Biophys. 48, 297-319 (2019).
  2. Rosenzweig, R., Kay, L. E. Bringing dynamic molecular machines into focus by methyl-TROSY NMR. Annu Rev Biochem. 83, 291-315 (2014).
  3. Palmer, A. G. Enzyme dynamics from NMR spectroscopy. Acc Chem Res. 48 (2), 457-465 (2015).
  4. Reif, B. Ultra-high resolution in MAS solid-state NMR of perdeuterated proteins: implications for structure and dynamics. J Magn Reson. 216, 1-12 (2012).
  5. Schanda, P., Ernst, M. Studying dynamics by magic-angle spinning solid-state NMR spectroscopy: Principles and applications to biomolecules. Prog Nucl Magn Reson Spectrosc. 96, 1-46 (2016).
  6. Le Marchand, T., et al. (1)H-H-detected biomolecular NMR under fast magic-angle spinning. Chem Rev. 122 (10), 9943-10018 (2022).
  7. Pervushin, K., Riek, R., Wider, G., Wuthrich, K. Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc Natl Acad Sci U S A. 94 (23), 12366-12371 (1997).
  8. Tzakos, A. G., Grace, C. R., Lukavsky, P. J., Riek, R. NMR techniques for very large proteins and RNAs in solution. Annu Rev Biophys Biomol Struct. 35, 319-342 (2006).
  9. Sprangers, R., Kay, L. E. Quantitative dynamics and binding studies of the 20S proteasome by NMR. Nature. 445 (7128), 618-622 (2007).
  10. Wright, P. E., Dyson, H. J. Intrinsically disordered proteins in cellular signalling and regulation. Nat Rev Mol Cell Biol. 16 (1), 18-29 (2015).
  11. van der Lee, R., et al. Classification of intrinsically disordered regions and proteins. Chem Rev. 114 (13), 6589-6631 (2014).
  12. Tompa, P. Intrinsically unstructured proteins. Trends Biochem Sci. 27 (10), 527-533 (2002).
  13. Dyson, H. J., Wright, P. E. Coupling of folding and binding for unstructured proteins. Curr Opin Struct Biol. 12 (1), 54-60 (2002).
  14. Uversky, V. N. Intrinsically disordered proteins in overcrowded milieu: Membrane-less organelles, phase separation, and intrinsic disorder. Current Opinion in Structural Biology. 44, 18-30 (2017).
  15. Patel, A., et al. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell. 162 (5), 1066-1077 (2015).
  16. Abyzov, A., Blackledge, M., Zweckstetter, M. Conformational dynamics of intrinsically disordered proteins regulate biomolecular condensate chemistry. Chem Rev. 122 (6), 6719-6748 (2022).
  17. Uversky, V. N. Unusual biophysics of intrinsically disordered proteins. Biochim Biophys Acta. 1834 (5), 932-951 (2013).
  18. Papoian, G. A. Proteins with weakly funneled energy landscapes challenge the classical structure-function paradigm. Proc Natl Acad Sci U S A. 105 (38), 14237-14238 (2008).
  19. Uversky, V. N., Gillespie, J. R., Fink, A. L. Why are "natively unfolded" proteins unstructured under physiologic conditions. Proteins. 41 (3), 415-427 (2000).
  20. Bah, A., et al. Folding of an intrinsically disordered protein by phosphorylation as a regulatory switch. Nature. 519 (7541), 106-109 (2015).
  21. Tompa, P., Schad, E., Tantos, A., Kalmar, L. Intrinsically disordered proteins: emerging interaction specialists. Curr Opin Struct Biol. 35, 49-59 (2015).
  22. Dyson, H. J., Wright, P. E. Perspective: the essential role of NMR in the discovery and characterization of intrinsically disordered proteins. J Biomol NMR. 73 (12), 651-659 (2019).
  23. Adamski, W., et al. A unified description of intrinsically disordered protein dynamics under physiological conditions using NMR spectroscopy. J Am Chem Soc. 141 (44), 17817-17829 (2019).
  24. Dobson, C. M. Protein folding and misfolding. Nature. 426 (6968), 884-890 (2003).
  25. Bertoncini, C. W., et al. Release of long-range tertiary interactions potentiates aggregation of natively unstructured alpha-synuclein. Proc Natl Acad Sci U S A. 102 (5), 1430-1435 (2005).
  26. Buell, A. K., et al. Solution conditions determine the relative importance of nucleation and growth processes in alpha-synuclein aggregation. Proc Natl Acad Sci U S A. 111 (21), 7671-7676 (2014).
  27. Salvi, N., Abyzov, A., Blackledge, M. Atomic resolution conformational dynamics of intrinsically disordered proteins from NMR spin relaxation. Prog Nucl Magn Reson Spectrosc. 102, 43-60 (2017).
  28. Schneider, R., Blackledge, M., Jensen, M. R. Elucidating binding mechanisms and dynamics of intrinsically disordered protein complexes using NMR spectroscopy. Curr Opin Struct Biol. 54, 10-18 (2019).
  29. Rezaei-Ghaleh, N., Blackledge, M., Zweckstetter, M. Intrinsically disordered proteins: from sequence and conformational properties toward drug discovery. Chembiochem. 13 (7), 930-950 (2012).
  30. Jensen, M. R., Salmon, L., Nodet, G., Blackledge, M. Defining conformational ensembles of intrinsically disordered and partially folded proteins directly from chemical shifts. J Am Chem Soc. 132 (4), 1270-1272 (2010).
  31. Camacho-Zarco, A. R., et al. NMR provides unique insight into the functional dynamics and interactions of intrinsically disordered proteins. Chem Rev. 122 (10), 9331-9356 (2022).
  32. Mittag, T., Forman-Kay, J. D. Atomic-level characterization of disordered protein ensembles. Curr Opin Struct Biol. 17 (1), 3-14 (2007).
  33. Dyson, H. J., Wright, P. E. Unfolded proteins and protein folding studied by NMR. Chem Rev. 104 (8), 3607-3622 (2004).
  34. Dyson, H. J., Wright, P. E. NMR illuminates intrinsic disorder. Curr Opin Struct Biol. 70, 44-52 (2021).
  35. Sugase, K., Dyson, H. J., Wright, P. E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 447 (7147), 1021-1025 (2007).
  36. Bessa, L. M., et al. The intrinsically disordered SARS-CoV-2 nucleoprotein in dynamic complex with its viral partner nsp3a. Sci Adv. 8 (3), eabm4034 (2022).
  37. Milles, S., Salvi, N., Blackledge, M., Jensen, M. R. Characterization of intrinsically disordered proteins and their dynamic complexes: From in vitro to cell-like environments. Prog Nucl Magn Reson Spectrosc. 109, 79-100 (2018).
  38. Salvi, N., Abyzov, A., Blackledge, M. Atomic resolution conformational dynamics of intrinsically disordered proteins from NMR spin relaxation. Prog Nucl Magn Reson Spectrosc. 102 - 103, 43-60 (2017).
  39. Gill, M. L., Byrd, R. A., Palmer, A. G. Dynamics of GCN4 facilitate DNA interaction: a model-free analysis of an intrinsically disordered region. Phys Chem Chem Phys. 18 (8), 5839-5849 (2016).
  40. Bertoncini, C. W., et al. Structural characterization of the intrinsically unfolded protein beta-synuclein, a natural negative regulator of alpha-synuclein aggregation. J Mol Biol. 372 (3), 708-722 (2007).
  41. Rezaei-Ghaleh, N., et al. Local and global dynamics in intrinsically disordered synuclein. Angew Chem Int Ed Engl. 57 (46), 15262-15266 (2018).
  42. Rezaei-Ghaleh, N., Parigi, G., Zweckstetter, M. Reorientational dynamics of amyloid-beta from NMR spin relaxation and molecular simulation. J Phys Chem Lett. 10 (12), 3369-3375 (2019).
  43. Palmer, A. G. NMR characterization of the dynamics of biomacromolecules. Chem Rev. 104 (8), 3623-3640 (2004).
  44. Palmer, A. G., Massi, F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem Rev. 106 (5), 1700-1719 (2006).
  45. Kay, L. E., Torchia, D. A., Bax, A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 28 (23), 8972-8979 (1989).
  46. Mittermaier, A., Kay, L. E. Review - New tools provide new insights in NMR studies of protein dynamics. Science. 312 (5771), 224-228 (2006).
  47. Abragam, A. . Principles of Nuclear Magnetism. , (1983).
  48. Ernst, R. R., Bodenhausen, G., Wokaun, A. . Principles of Nuclear Magnetic Resonance in One and Two Dimensions. , (1990).
  49. Cavanagh, J., Fairbrother, W. J., Palmer, A. G., Skelton, N. J. . Protein NMR Spectroscopy: Principles and Practice. , (1995).
  50. Levitt, M. H. . Spin Dynamics: Basics of Nuclear Magnetic Resonance. , (2008).
  51. Keeler, J. . Understanding NMR Spectroscopy. , (2010).
  52. Bloembergen, N., Purcell, E. M., Pound, R. V. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev. 73 (7), 679-712 (1948).
  53. Wangsness, R. K., Bloch, F. The dynamical theory of nuclear induction. Phys Rev. 89 (4), 728-739 (1953).
  54. Redfield, A. G. On the theory of relaxation processes. IBM J Res Dev. 1 (1), 19-31 (1957).
  55. Peng, J. W., Wagner, G. Mapping of the spectral densities of N-H bond motions in eglin c using heteronuclear relaxation experiments. Biochemistry. 31 (36), 8571-8586 (1992).
  56. Farrow, N. A., et al. Backbone dynamics of a free and a phosphopeptide-complexed src homology-2 domain studied by n-15 NMR relaxation. Biochemistry. 33 (19), 5984-6003 (1994).
  57. Tolman, J. R., Ruan, K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem Rev. 106 (5), 1720-1736 (2006).
  58. Mulder, F. A. A., Skrynnikov, N. R., Hon, B., Dahlquist, F. W., Kay, L. E. Measurement of slow (mu s-ms) time scale dynamics in protein side chains by N-15 relaxation dispersion NMR spectroscopy: Application to Asn and Gln residues in a cavity mutant of T4 lysozyme. J Am Chem Soc. 123 (5), 967-975 (2001).
  59. Tollinger, M., Skrynnikov, N. R., Mulder, F. A. A., Forman-Kay, J. D., Kay, L. E. Slow dynamics in folded and unfolded states of an SH3 domain. J Am Chem Soc. 123 (46), 11341-11352 (2001).
  60. Akke, M., Palmer, A. G. Monitoring macromolecular motions on microsecond to millisecond time scales by R(1)rho-R(1) constant relaxation time NMR spectroscopy. J Am Chem Soc. 118 (4), 911-912 (1996).
  61. Loria, J. P., Rance, M., Palmer, A. G. A relaxation-compensated Carr-Purcell-Meiboom-Gill sequence for characterizing chemical exchange by NMR spectroscopy. J Am Chem Soc. 121 (10), 2331-2332 (1999).
  62. Vallurupalli, P., Bouvignies, G., Kay, L. E. Studying "Invisible" excited protein states in slow exchange with a major state conformation. J Am Chem Soc. 134 (19), 8148-8161 (2012).
  63. Jeener, J., Meier, B. H., Bachmann, P., Ernst, R. R. Investigation of exchange processes by 2-dimensional NMR-spectroscopy. J Chem Phys. 71 (11), 4546-4553 (1979).
  64. Palmer, A. G., Kroenke, C. D., Loria, J. P. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 339, 204-238 (2001).
  65. Clore, G. M., Iwahara, J. Theory, practice, and applications of paramagnetic relaxation enhancement for the characterization of transient low-population states of biological macromolecules and their complexes. Chem Rev. 109 (9), 4108-4139 (2009).
  66. Iwahara, J., Clore, G. M. Detecting transient intermediates in macromolecular binding by paramagnetic NMR. Nature. 440 (7088), 1227-1230 (2006).
  67. Lakomek, N. A., et al. Residual dipolar couplings as a tool to study molecular recognition of ubiquitin. Biochem Soc Trans. 36 (Pt 6), 1433-1437 (2008).
  68. Johnson, C. N., Libich, D. S. Paramagnetic relaxation enhancement for detecting and characterizing self-associations of intrinsically disordered proteins. J Vis Exp. (175), e63057 (2021).
  69. Lakomek, N. A., Ying, J., Bax, A. Measurement of (1)(5)N relaxation rates in perdeuterated proteins by TROSY-based methods. J Biomol NMR. 53 (3), 209-221 (2012).
  70. Stief, T., Vormann, K., Lakomek, N. A. Sensitivity-enhanced NMR (15)N R(1) and R(1rho) relaxation experiments for the investigation of intrinsically disordered proteins at high magnetic fields. Methods. 223, 1-15 (2024).
  71. Kay, L. E., Keifer, P., Saarinen, T. Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J Am Chem Soc. 114 (26), 10663-10665 (1992).
  72. Geen, H., Freeman, R. Band-selective radiofrequency pulses. J Magn Reson (1969). 93 (1), 93-141 (1991).
  73. Desvaux, H., Berthault, P. Study of dynamic processes in liquids using off-resonance RF irradiation. Prog Nucl Magn Reson Spectrosc. 35 (4), 295-340 (1999).
  74. Overhauser, A. W. Polarization of nuclei in metals. Phys Rev. 91 (2), 476-476 (1953).
  75. Overhauser, A. W. Polarization of nuclei in metals. Phys Rev. 92 (2), 411-415 (1953).
  76. Kumari, P., Frey, L., Sobol, A., Lakomek, N. A., Riek, R. (15)N transverse relaxation measurements for the characterization of micros-ms dynamics are deteriorated by the deuterium isotope effect on (15)N resulting from solvent exchange. J Biomol NMR. 72 (3-4), 125-137 (2018).
  77. Karschin, N., Krenek, S., Heyer, D., Griesinger, C. Extension and improvement of the methanol-d(4) NMR thermometer calibration. Magn Reson Chem. 60 (4), 203-209 (2022).
  78. Sattler, M., Schleucher, J., Griesinger, C. Heteronuclear multidimensional NMR experiments for the structure determination of proteins in solution employing pulsed field gradients. Prog Nucl Magn Reson Spectrosc. 34 (2), 93-158 (1999).
  79. Ferrage, F., Cowburn, D., Ghose, R. Accurate sampling of high-frequency motions in proteins by steady-state N-{H} nuclear Overhauser effect measurements in the presence of cross-correlated relaxation. J Am Chem Soc. 131 (17), 6048-6049 (2009).
  80. Delaglio, F., et al. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 6 (3), 277-293 (1995).
  81. Skinner, S. P., et al. CcpNmr AnalysisAssign: a flexible platform for integrated NMR analysis. J Biomol NMR. 66 (2), 111-124 (2016).
  82. Lee, W., Tonelli, M., Markley, J. L. NMRFAM-SPARKY: enhanced software for biomolecular NMR spectroscopy. Bioinformatics. 31 (8), 1325-1327 (2015).
  83. Lee, W., Rahimi, M., Lee, Y., Chiu, A. POKY: a software suite for multidimensional NMR and 3D structure calculation of biomolecules. Bioinformatics. 37 (18), 3041-3042 (2021).
  84. Abyzov, A., et al. Identification of dynamic modes in an intrinsically disordered protein using temperature-dependent NMR relaxation. J Am Chem Soc. 138 (19), 6240-6251 (2016).
  85. Singh, A., Purslow, J. A., Venditti, V. 15N CPMG relaxation dispersion for the investigation of protein conformational dynamics on the micros-ms timescale. J Vis Exp. (170), e62395 (2021).
  86. Gopalan, A. B., Hansen, D. F., Vallurupalli, P. CPMG experiments for protein minor conformer structure determination. Methods Mol Biol. 1688, 223-242 (2018).
  87. Tugarinov, V., Kay, L. E. Methyl groups as probes of structure and dynamics in NMR studies of high-molecular-weight proteins. Chembiochem. 6 (9), 1567-1577 (2005).
  88. Lipari, G., Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J Am Chem Soc. 104 (17), 4546-4559 (1982).
  89. Lipari, G., Szabo, A. Model-Free Approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules .2. Analysis of experimental results. J Am Chem Soc. 104 (17), 4559-4570 (1982).
  90. Clore, G. M., et al. Deviations from the simple two-parameter model-free approach to the interpretation of nitrogen-15 nuclear magnetic relaxation of proteins. J Am Chem Soc. 112 (12), 4989-4991 (1990).
  91. Lemaster, D. M. Larmor frequency selective model free analysis of protein NMR relaxation. J Biomol NMR. 6 (4), 366-374 (1995).
  92. Peng, J. W., Wagner, G. Mapping of spectral density functions using heteronuclear NMR relaxation measurements. J Magn Reson (1969). 98 (2), 308-332 (1992).
  93. Farrow, N. A., Zhang, O. W., FormanKay, J. D., Kay, L. E. Characterization of the backbone dynamics of folded and denatured states of an SH3 domain. Biochemistry. 36 (9), 2390-2402 (1997).
  94. Khan, S. N., et al. Distribution of pico- and nanosecond motions in disordered proteins from nuclear spin relaxation. Biophys J. 109 (5), 988-999 (2015).
  95. Smith, A. A., Ernst, M., Meier, B. H., Ferrage, F. Reducing bias in the analysis of solution-state NMR data with dynamics detectors. J Chem Phys. 151 (3), 034102 (2019).
  96. Zumpfe, K., Smith, A. A. Model-free or not. Front Mol Biosci. 8, 727553 (2021).
  97. Robustelli, P., Trbovic, N., Friesner, R. A., Palmer, A. G. Conformational dynamics of the partially disordered yeast transcription factor GCN4. J Chem Theory Comput. 9 (11), 5190-5200 (2013).
  98. Salvi, N., Abyzov, A., Blackledge, M. Multi-timescale dynamics in intrinsically disordered proteins from NMR relaxation and molecular simulation. J Phys Chem Lett. 7 (13), 2483-2489 (2016).

Nachdrucke und Genehmigungen

Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden

Genehmigung beantragen

Weitere Artikel entdecken

NMR SpektroskopieStrukturdynamikProteine15N Relaxationglobul re Proteineintrinsische UnordnungTROSYEinblicke in atomare Aufl sungInterne Flexibilit tPikosekundenNanosekundenHetNOE ExperimenteDynamik des Proteinr ckgrats

This article has been published

Video Coming Soon

JoVE Logo

Datenschutz

Nutzungsbedingungen

Richtlinien

Kontakt

BIBLIOTHEKS-EMPFEHLUNG

JoVE-Newsletter

Forschung

Lehre

Autoren

Bibliothekare

ÜBER JoVE

Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten