Experimental and Data Analysis Workflow for Soft Matter Nanoindentation

Podsumowanie

The protocol presents a complete workflow for soft material nanoindentation experiments, including hydrogels and cells. First, the experimental steps to acquire force spectroscopy data are detailed; then, the analysis of such data is detailed through a newly developed open-source Python software, which is free to download from GitHub.

Streszczenie

Nanoindentation refers to a class of experimental techniques where a micrometric force probe is used to quantify the local mechanical properties of soft biomaterials and cells. This approach has gained a central role in the fields of mechanobiology, biomaterials design and tissue engineering, to obtain a proper mechanical characterization of soft materials with a resolution comparable to the size of single cells (μm). The most popular strategy to acquire such experimental data is to employ an atomic force microscope (AFM); while this instrument offers an unprecedented resolution in force (down to pN) and space (sub-nm), its usability is often limited by its complexity that prevents routine measurements of integral indicators of mechanical properties, such as Young's Modulus (E). A new generation of nanoindenters, such as those based on optical fiber sensing technology, has recently gained popularity for its ease of integration while allowing to apply sub-nN forces with µm spatial resolution, therefore being suitable to probe local mechanical properties of hydrogels and cells.

In this protocol, a step-by-step guide detailing the experimental procedure to acquire nanoindentation data on hydrogels and cells using a commercially available ferrule-top optical fiber sensing nanoindenter is presented. Whereas some steps are specific to the instrument used herein, the proposed protocol can be taken as a guide for other nanoindentation devices, granted some steps are adapted according to the manufacturer's guidelines. Further, a new open-source Python software equipped with a user-friendly graphical user interface for the analysis of nanoindentation data is presented, which allows for screening of incorrectly acquired curves, data filtering, computation of the contact point through different numerical procedures, the conventional computation of E, as well as a more advanced analysis particularly suited for single-cell nanoindentation data.

Wprowadzenie

The fundamental role of mechanics in biology is nowadays established^1,2. From whole tissues to single cells, mechanical properties can inform about the pathophysiological state of the biomaterial under investigation^3,4. For example, breast tissue affected by cancer is stiffer than healthy tissue, a concept that is the basis of the popular palpation test⁵. Notably, it has been recently shown that the coronavirus disease 2019 (COVID-19) caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is underlined by changes in the mechanical properties of blood cells, including decreased erythrocyte deformability and decreased lymphocyte and neutrophil stiffness as compared to blood cells from SARS-CoV-2-naïve individuals⁶.

In general, the mechanics of cells and tissues are inherently intertwined: each tissue has specific mechanical properties that simultaneously influence and depend on those of the constituent cells and extracellular matrix (ECM)⁵. Because of this, strategies to study mechanics in biology often involve engineering substrates with physiologically relevant mechanical stimuli to elucidate cell behavior in response to those stimuli. For example, the seminal work by Engler and colleagues demonstrated that mesenchymal stem cell linage commitment is controlled by matrix elasticity, as studied on soft and stiff two-dimensional polyacrylamide (PAAm) hydrogels⁷.

Many strategies to mechanically characterize the biomaterial under investigation exist, varying in spatial scale (i.e., local to bulk) and in the mode of deformation (e.g., axial vs shear), consequently yielding different information, which needs careful interpretation^3,8,9,10. The mechanics of soft biomaterials is commonly expressed in terms of stiffness. However, stiffness depends on both material properties and geometry, whereas elastic moduli are fundamental properties of a material and are independent of the material's geometry¹¹. As such, different elastic moduli are related to the stiffness of a given sample, and each elastic modulus encompasses the material's resistance to a specific mode of deformation (e.g., axial vs shear) under different boundary conditions (e.g., free expansion vs confinement)^11,12. Nanoindentation experiments allow the quantification of mechanical properties through the E which is associated with uniaxial deformation (indentation) when the biomaterial is not laterally confined^10,11,12.

The most popular method to quantify E of biological systems at the microscale is AFM^13,14,15,16. AFM is an extremely powerful tool with force resolution down to the pN level and spatial resolution down to the sub-nm scale. Further, AFM offers extreme flexibility in terms of coupling with complementary optical and mechanical tools, extending its capabilities to extract a wealth of information from the biomaterial under investigation¹³. Those attractive features, however, come with a barrier-to-entry represented by the complexity of the experimental set-up. AFM requires extensive training before users can acquire robust data, and its use for everyday mechanical characterization of biological materials is often unjustified, especially when its unique force and spatial resolutions are not required.

Because of this, a new class of nanoindenters has recently gained popularity due to their ease of use, while still offering AFM-comparable data with sub-nN force resolution and µm spatial resolution, reflecting forces exerted and perceived by cells over relevant length scales². Particularly, ferrule-top nanoindentation devices based on optical fiber sensing technology^17,18 have gained popularity among researchers active in the field of mechanobiology and beyond; and a wealth of works reporting the mechanical properties of biomaterials using these devices, including cells^19,20, hydrogels^8,21, and tissues^22,23 have been published. Despite the capabilities of these systems to probe local dynamic mechanical properties (i.e., storage and loss modulus), quasi-static experiments yielding E remain the most popular choice^8,19,20,21. In brief, quasi-static nanoindentation experiments consists of indenting the sample with a constant speed up to a set-point defined either by a maximum displacement, force, or indentation depth, and recording both the force and the vertical position of the cantilever in so-called force-distance (F-z) curves. F-z curves are then converted into force-indentation (F-δ) curves through the identification of the contact point (CP), and fitted with an appropriate contact mechanics model (usually the Hertz model¹³) to compute E.

While the operation of ferrule-top nanoindenters resembles AFM measurements, there are specificities worth considering. In this work, a step-by-step guide to robustly acquire F-z curves from cells and tissue-mimicking hydrogels using a commercially available ferrule-top nanoindenter is provided, in order to encourage standardization of experimental procedures between research groups using this and other similar devices. In addition, advice on how to best prepare hydrogel samples and cells to perform nanoindentation experiments is given, together with troubleshooting tips along the experimental pathway.

Furthermore, much of the variability in nanoindentation results (i.e., E and its distribution) depends on the specific procedure used to analyze data, which is non-trivial. To address this issue, instructions for the use of a newly developed open-source software programmed in Python and equipped with a user-friendly graphical user interface (GUI) for batch analysis of F-z curves are provided. The software allows for fast data screening, filtering of data, computation of the CP through different numerical procedures, the conventional computation of E, as well a more advanced analysis named the elasticity spectra²⁴, allowing to estimate the cell's bulk Young's modulus, actin cortex's Young's modulus, and actin cortex's thickness. The software can be freely downloaded from GitHub and can be easily adapted to analyze data originating from other systems by adding an appropriate data parser. It is emphasized that this protocol can be used for other ferrule-top nanoindentation devices, and other nanoindentation devices in general, granted some steps are adapted according to the specific instrument's guidelines. The protocol is schematically summarized in Figure 1.

Protokół

1. Preparation of substrates/cells for nanoindentation measurements

1. Follow the steps given in the Supplementary Protocol for preparation of PAAm hydrogels/cells for nanoindentation experiments. The procedure is summarized in Figure 2.
   NOTE: PAAm hydrogels have been chosen as they are the most common hydrogels used within the field of mechanobiology. However, the protocol is equally applicable to any type of hydrogel²⁵ (see Discussion, modifications of the method).

2. Starting up the device, probe choice, and probe calibration

1. Follow the steps given in the Supplementary Protocol for starting up the device. For technical details on the operation of optical fiber ferrule-top nanoindenters, check these references^17,18.
2. Select the nanoindentation probe as described below.
   NOTE: All commercially available probes such as the ones used in this protocol are equipped with a spherical tip (Figure 3A). Therefore, the choice narrows down to two variables: cantilever's stiffness and tip radius (Figure 3B).
   1. Choose a cantilever's stiffness (k in N/m) that matches the expected sample stiffness for best results¹⁵ (see Figure 3C and Discussion, critical steps in the protocol). For cells, select a probe with k in the range 0.01-0.09 N/m. For hydrogels, select a probe with k in the range 0.1-0.9 N/m, which yields optimal results for gels with expected E between a few kPa and 100 kPa (see Representative Results).
   2. Choose the tip radius (R in μm) according to the desired spatial resolution of the indentation process. For small cells such as Human Embryonic Kidney 293T (HEK293T) cells (average diameter of ~10-15 μm²⁶) select a sphere with R = 3 μm. For hydrogels, select a sphere with R = 10-250 μm to probe the biomaterial's mechanical properties over a large contact area and avoid local heterogeneities.
   3. Consult Figure 3C and any additional manufacturer's guidelines to select the appropriate probe.
3. Once the probe has been selected, follow the steps in the Supplementary Protocol to mount it on the nanoindenter.

3. Probe calibration

NOTE: The following steps are specific to ferrule-top nanoindentation devices based on optical fiber sensing technology, and they are detailed for software version 3.4.1. For other nanoindentation devices, follow the steps recommended by the device manufacturer.

1. On the software's main window, click on Initialize. A calibration menu will appear. Enter the probe details (can be found on the side of the probe's box; k in N/m, R in µm, and the calibration factor in air) in the input boxes.
2. Prepare the calibration dish: a thick glass Petri dish with a flat bottom (see Discussion, critical steps in the protocol). Fill the dish with the same medium as the sample dish (this can also be air). Match the temperature of the medium with that of the sample.
3. Place the calibration dish under the probe. If required, slide out the probe from the nanoindenter's arm holder and hold it in one hand to make space for placement of the calibration dish. Slide back the probe into place.
4. Perform the next two steps for calibration in liquid. If measuring in air, use the provided polytetrafluoroethylene substrate for calibration and skip to step 5.
   1. Prewet the probe with a drop of 70% ethanol using a Pasteur pipette with the end of the pipette in light contact with the glass ferrule, for the drop to slide over the cantilever and spherical tip²⁷ (see Discussion, critical steps in the protocol).
   2. Manually slide the nanoindenter's arm downwards until the probe is fully submerged, but still far away from the bottom of the Petri dish. If required, add more medium to the calibration dish. Wait 5 min so that equilibrium conditions are reached in the liquid.
5. In the software's Initialize menu, click on Scan Wavelength. The interferometer’s screen will show a progress bar and the Live Signal window on the computer’s software will display the pattern shown in Figure S1A, left. To check whether the optical scan was successful, navigate to the Wavelength Scan panel on the interferometer box. If successful, a sine wave should be visible (Figure 1A, right). See Discussion (troubleshooting of the method) if an error appears.
6. In the Initialize menu, click on Find Surface, which will progressively lower the probe until a set threshold in the cantilever's bending is reached. The probe stops moving when contact with the glass Petri dish is made.
7. Check whether the probe is in contact with the surface. Move the probe down by 1 µm using the y downwards arrow button on the software's main window. Observe the green signal (cantilever's deflection) in the Live Window of the software for changes in the baseline with each step, when the cantilever is in contact with the substrate (Figure S1B). If there is no change, the cantilever is not in contact (see next step).
8. Increase the Threshold value in the Options menu under the Find Surface tab from its default value of 0.01 by a step of 0.01 at a time and repeat the Find Surface step until in contact. Alternatively, bring down the probe to contact in small 1 µm steps until the green baseline starts shifting at each downwards step.
   NOTE: For the softest cantilevers (k = 0.025 Nm^-1), increase the Threshold value in the Options menu under the Find Surface tab a priori of performing step 6. Start from a threshold value of 0.06 or 0.07 and increase it up to 0.1 if necessary. This is because environmental noise will likely cause the cantilever to bend above the threshold prior to contact. For soft probes, decreasing the Approach Speed (μm/s) in the same menu also improves the procedure.
9. In the Initialize menu, click on Calibrate.
10. Check the Live Signal window of the software and make sure that both piezo's displacement and cantilever's deflection signals move up at the same time (​Figure S1C).
    1. If there is a mismatch in time, the probe is not fully in contact with the glass. Move down the probe at steps of 1 µm until the baseline of the cantilever signal changes (see step 7) and repeat step 9.
    2. If the cantilever signal does not change at all during the Calibrate step, then the probe is far from the surface. Increase the contact threshold iteratively (see step 8) until the surface is found correctly and repeat calibration from the beginning starting with the wavelength scan.
11. When the calibration is complete, check the old and new calibration factors on the pop-up window displayed. If the new calibration factor is in the correct range, click on Use New Factor. If calibration fails, and the new factor is either NaN or is not in the expected range, see Discussion (troubleshooting of the method) for resolution.
    NOTE: The new factor should be ~n times lower than the one provided on the probe's box if the calibration was performed in a liquid medium with refractive index n (n = 1.33 for water). If calibration was performed in air, then the new and old calibration factors should be approximately equal.
12. Check whether the demodulation circle has been correctly calibrated as follows. Navigate to the Demodulation tab on the interferometer desktop. Gently tap on the optical table or on the nanoindenter to induce enough noise. A white circle made up of discrete data points should approximately cover the red circle (Figure S1D).
13. If the white circle does not overlap with the red circle, or a warning appears on the interferometer's display, the demodulation circle needs recalibration. This can be done in two ways as described below.
    1. Continuously tap on the body of the nanoindenter to induce one full circle of noise and press the Calibrate button on the interferometer.
    2. Enter in contact with the glass substrate and press Calibrate from the Initialize menu of the software's main window. Do not save the calibration factor. At this point, check again and make sure the white circle overlaps with the red circle.
       NOTE: If the signal is not just slightly displaced from the demodulation circle but rather became very small or is not visible at all, it means that the cantilever is stuck to the optical fiber. Follow the troubleshooting advice for this problem (see Discussion, troubleshooting of the method) and repeat either steps 13.1 or 13.2. Once the cantilever gets back to its horizontal position (Figure 3A), the signal will recover to the demodulation circle.
14. Verify the calibration by performing an indentation on the glass substrate directly after the calibration as described below.
    1. Load or make an experiment file by clicking on Configure Experiment and add a Find Surface step and Indentation step. For the indentation step, use the default displacement mode settings and change the maximum displacement to the calibration distance (3,000 nm) to displace the probe against the stiff substrate.
    2. Click on Run Experiment and check the demodulation circle in the interferometer window. Check the white signal and make sure it is on top of the red circle during indentation.
    3. Check the results on the software's main window in the Time Data graph, and make sure the piezo's displacement (blue line) is equal to the cantilever's deflection (green line) as the indentation starts in contact and no material deformation is expected. If the signals are not parallel, see Discussion (troubleshooting of the method).
15. Change the local path in the calibration menu by setting the Calibration Save Path to an appropriate directory.
16. When the probe has been successfully calibrated, move the piezo up by 500 μm.

4. Measuring the Young's Modulus of soft materials

1. Nanoindentation of hydrogels
   1. Load the Petri dish containing the sample(s) on the microscope's stage and manually move the nanoindenter's probe to a desired x-y position above the sample.
   2. Manually slide the probe in solution, taking care to leave 1-2 mm between the probe and the sample's surface at this stage. Wait 5 min for the probe to equilibrate in the medium.
   3. Focus the z plane of the optical microscope so that the probe is clearly visible.
   4. Perform a single indentation to tune the experimental parameters as described below.
      1. Configure a new experiment in the software's main window. Click on Configure Experiment, which will open a new window. Add a Find Surface step. All parameters of the Find Surface step can be changed in the Options menu of the software if required.
         NOTE: The Find Surface will lower the probe until the surface is found, and then it will retract the probe to a distance defined by Z Above Surface (µm), above the sample's surface. If the selected cantilever is too stiff for the sample or the sample is sticky, after the step the probe is likely to still be in contact with the sample, which will result in a curve without a baseline (Figure 4C). To solve this problem, increase the Z Above Surface (µm).
      2. Add an Indentation step. Select the Profile tab and click on Displacement Control. Leave the default indentation profile.
      3. Click on Run Experiment on the main software window. This will find the surface and perform a single indentation.If the single indentation does not look as expected, adjust the experimental parameters as outlined in Figure 4 and Discussion (troubleshooting of the method).
   5. Once the indentation looks as desired, configure the matrix scan so that a sufficient area of the sample will be indented. Click on Configure Experiment, add a Find Surface step with the previously determined experimental parameters and add a Matrix Scan step.
   6. For flat hydrogels, configure a matrix scan containing 50-100 points (i.e., 5 x 10 or 10 x 10 in x and y) spaced at 10-100 µm (i.e., dx = dy = 10-100 µm). Click on Use Stage Position to start the matrix scan from the current stage position. Make sure the Auto Find Surface box is ticked to find the surface at each indentation using the set experimental parameters.
      1. To avoid oversampling, set the step size to at least twice the contact radius (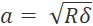, where δ is the indentation depth).
      2. Set up the matrix scan profile in displacement control. Ensure that the profile does not violate the assumptions of the Hertz model (see Discussion, critical steps in the protocol).
      3. Leave the number of segments to 5, which is the default value, and use the default displacement profile. If necessary, change the displacement profile in terms of maximum displacement and time for each sloped segment, which will affect the maximum indentation depth and the strain rate, respectively. Do not exceed strain rates > 10 μm/s (see Discussion, limitations of the method).
      4. Enter a value for the approach speed, which determines how fast the probe is displaced toward the sample before contact. Match the retraction speed to the approach speed (see note below).
         NOTE: For soft cantilevers and noisy environments, an approach speed of 1,000-2,000 nm/s is recommended. For stiffer cantilevers and controlled environments, this can be increased.
      5. Save the configured experiment in the desired Experiment Path and select a directory where the data will be saved in the Save Path, in the General tab of the Configure Experiment window. Click on Run Experiment.
   7. Once the matrix scan is completed, raise the probe by 200-500 µm and move the probe to a different area of the sample sufficiently far away from the first area.
   8. Repeat the experiment at least two times so that sufficient data is acquired on each sample (i.e., at least two matrix scans per sample, containing 50-100 curves each).
2. Nanoindentation of cells
   1. Load the sample on the microscope as described above.
   2. For single-cell indentation, focus the z plane so that both cells and probe are visible at 20x or 40x magnification, depending on cell size and spreading.
   3. Move the probe above the cell to be indented.
   4. Configure a new experiment in the software's main window. Click on Configure Experiment, which will open a new window. Add a Find Surface and Indentation step with default parameters in displacement mode.
   5. Click on Run Experiment, which will find the surface and perform a single indentation. Check whether the indentation was successful. If the curve does not look as expected, adjust the experimental parameters (see Figure 4 and Discussion, troubleshooting of the method).
   6. If the indentation was successful, add a matrix scan to the experiment. Follow the steps given for hydrogels' nanoindentation experiments; configure the matrix scan so that the step size allows for a small area of the cell to be indented; 25 points spaced at 0.5-5 µm for HEK293T cells.
      1. Depending on the cell size, adapt the matrix scan to ensure the tip does not indent outside the cell limit, i.e., doing a different map geometry or probing fewer points.
   7. Click on Run Experiment and wait for it to be completed.
   8. Once the matrix scan is completed, raise the probe out of contact (50 µm in the z plane).
   9. Move the probe above a new cell and repeat the process (see Discussion, critical steps in the protocol).
3. Cleaning the probe and switching off the instrument
   1. Follow the steps given in the Supplementary Protocol to clean the probe and switch off the nanoindentation device.

5. Data analysis

1. Downloading and installing the software
   1. Follow the steps given in the Supplementary Protocol to download and install the software for data analysis^28,29.
2. Screening F-z curves and production of cleaned data set in JSON format
   1. Launch prepare.py from the command line on the lab computer as outlined in steps 2 to 3.
   2. If using a Windows computer, hold the shift key while right-clicking on the NanoPrepare folder and click on Open PowerShell Window Here. Type the python prepare.py command and press the Enter key. A GUI will pop up on your screen (Figure S2).
   3. If using a MacOS computer, right-click on the NanoPrepare folder and click on New Terminal at Folder. Type the python3 prepare.py command and press the Enter key, which will launch the GUI (Figure S2).
   4. Select the O11NEW data format from the drop-down list. If data is not loaded correctly, then relaunch the GUI and select O11OLD.
      NOTE: The O11NEW format works for data obtained using ferrule-top optical fiber sensing nanoindentation devices with software version 3.4.1. This format will also work for previous software versions, at least those belonging to nanoindenters installed in 2019-2020.
   5. Click on Load Folder. Select a folder containing the data to be analyzed-single matrix scan or multiple matrix scans. The top graph (Raw Curves) will be populated with the uploaded data set. To visualize a specific curve, click on it. This will highlight it in green and show it on the bottom graph (Current Curve).
   6. Clean the data set using the tabs present on the right part of the GUI as outlined below.
      1. Use the Segment button to select the correct segment to be analyzed, which is the forward segment of F-z curves. The specific number depends on the number of segments selected in the nanoindentation software when performing experiments.
      2. Use the Crop 50 nm button to crop the curves by 50 nm at the extreme left (if L is ticked), right (if R is ticked), or both sides (if both R and L are ticked). Click this button several times to crop as much as is required. Use this to remove artifacts present at the start/end of F-z curves.
      3. Inspect the Cantilever tab for the spring constant, tip geometry, and tip radius. Inspect the tab to ensure that the metadata has been read correctly.
      4. Use the Screening tab to set a force threshold that will discard all the curves that did not reach the given force. Discarded curves will be highlighted in red.
      5. Use the Manual Toggle button to manually remove curves that have not been correctly acquired. Remove any curves by clicking on the specific curve and selecting OUT, which will highlight the curve in red.
   7. Click on Save JSON. Enter an appropriate name for the cleaned data set, which is a single JSON file. Send the JSON file to the computer where the NanoAnalysis software was installed.

6. Formal data analysis

1. Launch the nano.py file from the command line by navigating to the NanoAnalysis folder and launching a terminal as previously explained. Type the python nano.py or python3 nano.py command (depending on the operating system) and press the Enter key. A GUI will pop up on your screen (Figure S3).
2. On the top left of the GUI, click on Load Experiment and select the JSON file. This will populate the file list and the Raw Curves graph showing the data set in terms of F-z curves. Both F and z axes are shown relative to the CP coordinates, which are computed in the background when loading the dataset (see the following note). In the Stats box, check the values of the three parameters: N_activated, N _failed, and N_excluded.
   NOTE: N_activated represents the number of curves that will be analyzed in the subsequent Hertz/elasticity spectra analysis and appear in black in the Raw Curves graph. N_failed represents the number of curves on which a reliable CP could not be found and appear in blue in the graph. These curves will automatically be discarded in the subsequent analysis. Upon opening the software, some curves may be automatically moved to the failed set. This is because the CP is calculated upon opening the software with the default Threshold algorithm (see below). N_excluded represents the curves that are manually selected to be excluded from the analysis and will appear in red in the graph (see below).
3. Check whether the number of failed, excluded, and activated curves is reasonable. Check the Raw Curves graph to visualize the curves.
4. To visualize a specific curve in more detail, click on it. This will highlight it in green and show it on the Current Curve graph. Once a single curve has been selected, the R and k parameters (which must be the same for all curves) will be populated in the Stats box of the GUI.
5. Change the status of a given curve using the Toggle box. Click on the specific curve you want to change the status of, and then click on either Activated, Failed, or Excluded. The count in the Stats box is automatically updated.
   NOTE: To change the view of the data set in the Raw Curves graph use the View box. Click on All to show all curves (i.e., activated, failed, and excluded in the respective colors). Click on Failed to show the activated and the failed curves and click on Activated to only show the activated curves. To reset the status of all curves between activated and excluded, click on Activated or Excluded in the Reset box.
6. Once the dataset has been further cleaned, follow the data analysis pipeline outlined below.
   1. Filter any noise present in the curves using the filters implemented in the GUI (Filtering Box), namely, a custom filter called Prominency filter, the Savitzky Golay^30,31 (SAVGOL) filter, and a smoothing filter based on computing the median of the data in a given window (median filter). See Discussion (critical steps in the protocol) for details on filters.
   2. Inspect the filtered curves in the Current Curve graph. The filtered curve is shown in black whereas the non-filtered version of the curve is shown in green.
      NOTE: It is advised to filter the data as little as possible to preserve features of the original signal. Over filtering may smooth out any differences present in the data. Working with the prominency filter activated is enough for the Hertz analysis of nanoindentation data. If the data is particularly noisy, then a SAVGOL or median filters may be additionally applied.
   3. Select an algorithm to find the CP. In the Contact Point box, choose one of a series of numerical procedures that have been implemented in the software, namely, the Goodness of Fit (GoF)³², Ratio of Variances (RoV)³², Second derivative³³, or Threshold³³. See Discussion, critical steps in the protocol for details on the algorithms.
      NOTE: The CP is the point at which the probe comes into contact with the material and needs to be identified in order to convert F-z data into F-δ data (for soft materials, δ is finite and needs to be calculated). The selected algorithm will be applied to all active curves of the data set, and curves where the algorithm fails to locate the CP robustly will be moved to the failed set.
   4. Adjust the algorithm's parameters to suit your dataset so that the CP is located correctly as detailed in the Discussion, critical steps in the protocol.To view where the CP has been found on a single curve, select the curve by clicking on it and click on Inspect. Check the pop-up window that appears to identify where the CP has been located.
   5. Check whether the red line that appears, which is the parameter the algorithm computed in the selected region of interest, has a maximum or minimum value that corresponds to the location of the CP (e.g., for the GoF, the parameter is the R²). Repeat this process for all curves if needed.
      NOTE: The axes of the pop-up are in absolute coordinates so that the location of the CP can be shown. Conversely, the axes of the Raw Curves and Current Curve graph are shown relative to the CP, i.e., the location of the CP is (0,0).
   6. Click on Hertz Analysis. This will generate three graphs described below.
      1. Check individual F-δ curves in the dataset together with the average Hertz fit (red dashed line). Adjust the indentation in nm up to which the Hertz model is fitted in the Results box under Max Indentation (nm). Set it to a maximum of ~10% of R for the Hertz model to be valid (see Discussion, critical steps in the protocol).
      2. Check the average F-δ curve with error band showing one standard deviation (SD) together with the average Hertz fit (red dashed line). Visualize the average Hertz fit on the Raw Curves graph for reference and the Hertz fit for each curve on the Current Curve.
      3. Check the scatter plot of E originating from fitting the Hertz model to each individual curve.
   7. Click on either the file name, F-z curve, F-δ curve, or a point on the scatter plot to highlight the curve in each plot. If a data point in the scatter plot appears to lie outside the distribution of the data, click on it and inspect the curve to which it belongs. Verify that the CP has been located correctly by clicking on the Inspect button. Exclude the curve from the analysis if necessary.
   8. Inspect the Results box for the computed mean E and its SD (E_γ ± σ) and make sure they are reasonable for the given experiment.
   9. In the Save box, click on Hertz. In the pop-up window, enter file name and directory. Once done, click on Save. A .tsv file will be created. Open the .tsv file in any additional software of preference and use the values for statistical analysis and further plotting.
      NOTE: The file contains the E obtained from each curve and the mean E and its SD. Additionally, the file contains metadata associated with the analysis, including the number of curves analyzed, R, k, and the maximum indentation used for the Hertz model.
   10. This step is optional. Click on Average F-Ind to export the average force and the average indentation, together with one SD in the force.
   11. For cell nanoindentation data, click on Elasticity Spectra Analysis (see Representative Results and Discussion). Inspect the two plots produced, namely, E as a function of the indentation depth (E(δ)) for each curve, and the average E(δ) with error band showing one SD (solid red line and shaded area) fitted by a model (black dashed line), which allows to estimate the cell's actin cortex's Young's modulus, the cell's bulk Young's modulus, and the actin cortex's thickness. Additionally, check the average E(δ) in the top graph in red.
   12. Make sure the Interpolate box is checked, which ensures the derivative needed to perform the elasticity spectra analysis is computed on the interpolated signal (see Representative Results).
   13. Inspect the Results box, reporting the cortex's Young's modulus (E₀ ± σ), the cell's bulk Young's modulus (E_b ± σ), and the cortex thickness (d₀ ± σ).
       NOTE: The average elasticity spectra may appear noisy at first, with prominent sinusoidal oscillations. As a result, equation (3) may not be fitted correctly. If this is the case, iteratively increasing the window length of the smoothing SAVGOL filter³⁴ solves this issue.
   14. Once the analysis is finished, click on ES in the Save box. This will export a .tsv file in the specified directory, containing the average elasticity as a function of the average indentation depth and contact radius, the metadata associated with the experiment (see above), and the estimated model parameters explained above. Finally, the average elasticity disregarding the dependency on δ and its SD, are also reported.
   15. Close the software and input the saved results in any other software of preference to further plot the data and perform statistical analysis.
   16. This step is optional: Export graphs from the GUI by right-clicking on the graph and selecting Export. Export the graph in .svg, so that parameters such as font, font size, line style, etc. can be edited in another software of choice. 
       NOTE:Custom CP algorithms and filters can be programmed and added to the already existing ones. See Supplementary Note 1 for details.

Wyniki

Following the protocol, a set of F-z curves is obtained. The dataset will most likely contain good curves, and curves to be discarded before continuing with the analysis. In general, curves should be discarded if their shape is different from the one shown in Figure 4A. Figure 5AI shows a dataset of ~100 curves obtained on a soft PAAm hydrogel of expected E 0.8 KPa³⁵ uploaded in the NanoPrepare GUI. Most curves present a...

Dyskusje

This protocol shows how to robustly acquire force spectroscopy nanoindentation data using a commercially available ferrule-top nanoindenter on both hydrogels and single cells. In addition, instructions for the use of an open-source software programmed in Python comprising a precise workflow for the analysis of nanoindentation data are provided.

Critical steps in the protocol
The following steps have been identified to be of particular importance when following this proto...

Materiały

Name	Company	Catalog Number	Comments
12 mm coverslips	VWR	631-1577P
35 mm cell treated culture dishes	Greiner CELLSTAR	627160
Acrylamide	Sigma-Aldrich	A4058
Acrylsilane	Alfa Aesar	L16400
Ammonium Persulfate	Merk	7727-54-0
Bisacrylamide	Merk	110-26-9
Chiaro nanoindenter	Optics 11 Life		no catologue number
Ethanol			general
Fetal bovine serum	Gibco	16140071
High glucose DMEM	Gibco	11995065
Isopropanol			general
Kimwipe	Kimberly Clark	21905-026
Microscope glass slides	VWR	631-1550P
MilliQ system	Merk Millipore	ZR0Q008WW
OP1550 Interferometer	Optics11 Life		no catalogue number
Optics 11 Life probe (k = 0.02-0.005 N/m, R = 3-3.5 um)	Optics 11 Life		no catologue number
Optics 11 Life probe (k = 0.46-0.5 N/m, R = 50-55 um)	Optics 11 Life		no catologue number
Penicillin/Streptomycin	Gibco	15140122
RainX rain repellent	RainX	26012
Standard petri dishes (90 mm)	Thermo Scientific	101RTIRR
Tetramethylethylenediamine	Sigma-Aldrich	110-18-9
Vaccum dessicator	Thermo Scientific	531-0250
Software
Data acquisition software (v 3.4.1)	Optics 11 Life
GitHub Desktop (Optional)	Microsoft
Python 3	Python Software Foundation
Visual Studio Code (Optional)	Microsoft